
Actualización : Hemos introducido una App de aprendizaje interactivo para el aprendizaje automático / AI ,>> Compruébalo gratis ahora <<
Importa las librerías necesarias
import numpy as np
import pandas as pd
eps = np.finfo(float).eps
from numpy import log2 as log
‘eps’ aquí es el menor número representable. A veces nos sale log(0) o 0 en el denominador, para evitarlo vamos a usar esto.
Definir el conjunto de datos:
Crear el dataframe de pandas :
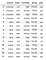
Ahora vamos a intentar recordar los pasos para crear un árbol de decisión….
1.compute the entropy for data-set2.for every attribute/feature:
1.calculate entropy for all categorical values
2.take average information entropy for the current attribute
3.calculate gain for the current attribute3. pick the highest gain attribute.
4. Repeat until we get the tree we desired
- Encuentra la Entropía y luego la Ganancia de Información para dividir el conjunto de datos.
Definiremos una función que toma en clase (vector de variables objetivo) y encuentra la entropía de esa clase.
Aquí la fracción es ‘pi’, es la proporción de un número de elementos en ese grupo dividido al número de elementos en el grupo antes de la división (grupo padre).

2 .Ahora define una función {ent} para calcular la entropía de cada atributo :
almacena la entropía de cada atributo con su nombre :
a_entropy = {k:ent(df,k) for k in df.keys()}
a_entropy

3. calcular la ganancia de información de cada atributo :
definir una función para calcular IG (infogain) :
IG(attr) = entropía del conjunto de datos – entropía del atributo
def ig(e_dataset,e_attr):
return(e_dataset-e_attr)
almacenar IG de cada attr en un dict :
#entropy_node = entropy of dataset
#a_entropy = entropy of k(th) attrIG = {k:ig(entropy_node,a_entropy) for k in a_entropy}

como podemos ver outlook tiene la mayor ganancia de información de 0.24 , por lo tanto seleccionaremos outook como el nodo de este nivel para la división.
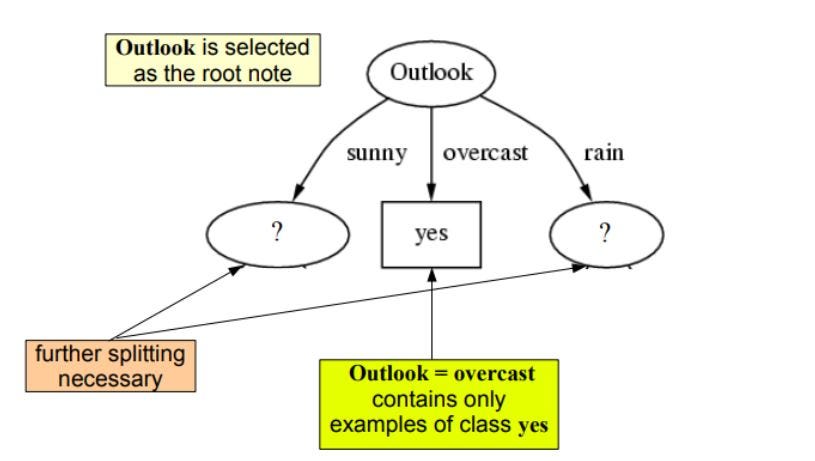
Ahora para proceder con nuestro árbol usaremos la recursión
Repetimos lo mismo para los subárboles hasta obtener el árbol.

Construimos un árbol de decisión basado en esto. A continuación el código completo.

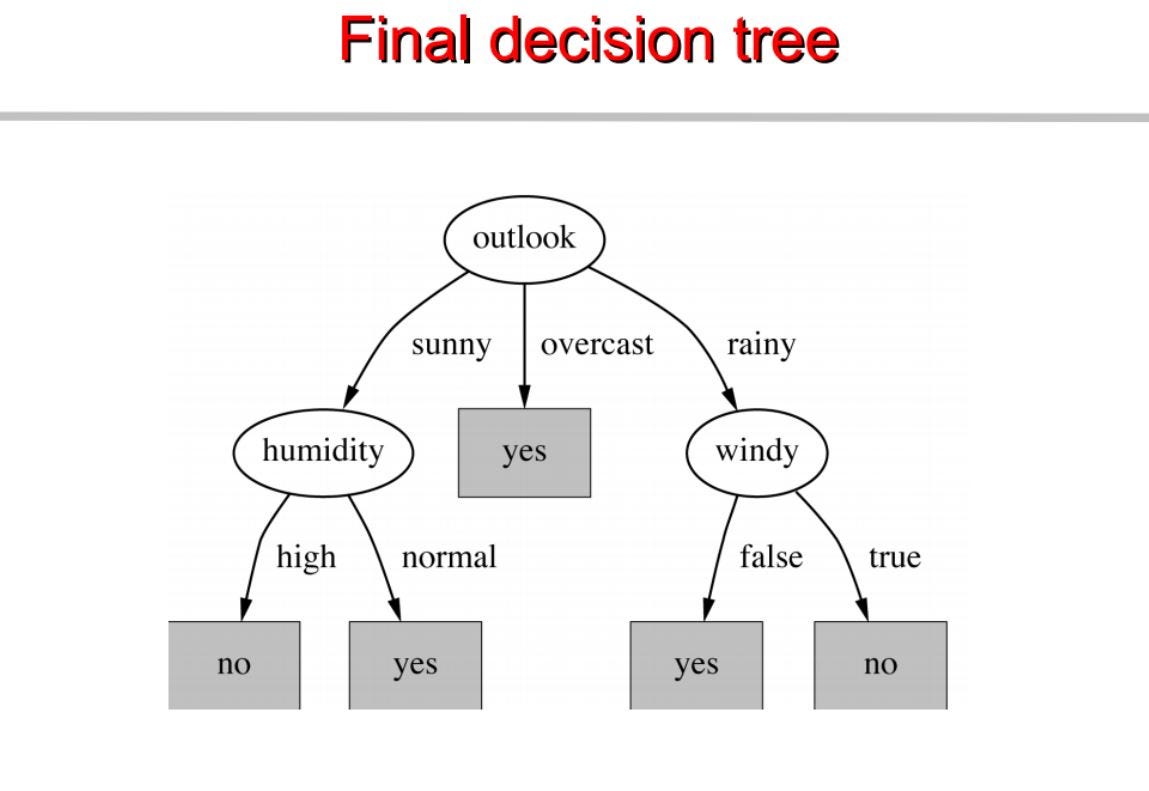
visita pytholabs.com para cursos increíbles
.