Multiplicación de grupos
Ahora investigaremos qué ocurre cuando aplicamos dos operaciones de simetría en secuencia. Como ejemplo, consideremos la molécula \(NH_3\), que pertenece al grupo puntual \(C_{3v}\). Consideremos lo que sucede si aplicamos una rotación \(C_3\) seguida de una reflexión \(\sigma_v\). Escribimos esta operación combinada \(\sigma_v\)\N-(C_3\) (cuando se escriben, las operaciones de simetría operan sobre lo que está directamente a su derecha, al igual que los operadores en la mecánica cuántica – por lo tanto, tenemos que trabajar hacia atrás de derecha a izquierda de la notación para obtener el orden correcto en el que se aplican los operadores). Como pronto veremos, el orden en el que se aplican las operaciones es importante.
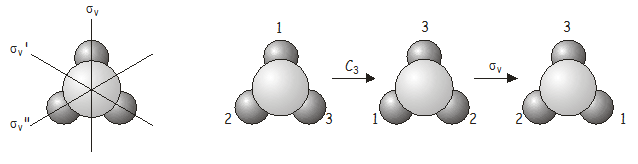
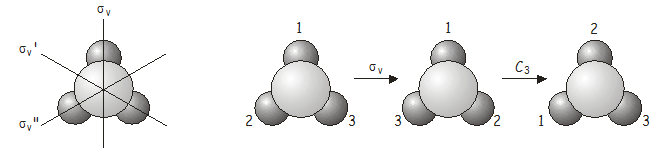
De nuevo, la operación combinada \(C_3\)\️ (\️) es equivalente a otra operación del grupo de puntos, esta vez \️ (\️).
Hay dos puntos importantes que se ilustran con este ejemplo:
Los efectos de aplicar dos operaciones de simetría en secuencia dentro de un grupo puntual dado se resumen en tablas de multiplicación de grupos. Como ejemplo, a continuación se muestra la tabla de multiplicación de grupos completa para \(C_{3v}\) utilizando las operaciones de simetría como se define en las figuras anteriores. Las operaciones escritas a lo largo de la primera fila de la tabla se llevan a cabo en primer lugar, seguido de los escritos en la primera columna (tenga en cuenta que la tabla cambiaría si optamos por nombrar \(\sigma_v’\), \(\sigma_v’\) y \(\sigma_v»\) en algún orden diferente).