Alai

Michael Fowler,UVa Physics.

El ímpetu tiene dirección

Como comentamos en la última conferencia, incluso antes de que Newton formulara sus leyes, Descartes, con un poco de ayuda de Huygens, había descubierto una profunda verdad dinámica: en cualquier colisión, o de hecho en cualquier interacción de cualquier tipo, la cantidad total de «ímpetu» -una medida del movimiento- siempre era la misma. El momento de un objeto en movimiento se define como el producto de la masa y la velocidad, y por tanto es un vector: tiene magnitud y dirección. Si estás sobre unos patines sin fricción y lanzas una pelota, te mueves hacia atrás: tienes un momento de magnitud igual, pero de dirección opuesta, al de la pelota, por lo que el momento total (el tuyo más el de la pelota) sigue siendo cero. Los cohetes funcionan de la misma manera, lanzando material a gran velocidad. No funcionan «empujando contra el aire», funcionan empujando contra el material que expulsan, igual que tú empujas contra un balón que estás lanzando, y éste te empuja hacia atrás, provocando tu aceleración.

Si todavía sospecha que los cohetes realmente empujan contra el aire, recuerde que funcionan igual de bien en el espacio. De hecho, la opinión generalizada era que cuando Goddard, uno de los primeros cohetes estadounidenses (el Centro de Vuelo Espacial Goddard lleva su nombre) hablaba de cohetes en el espacio, estaba perdiendo el tiempo. En un editorial del New York Times de 1921 se decía: «El profesor Goddard no es un hombre de negocios: «El profesor Goddard no conoce la relación entre acción y reacción y la necesidad de tener algo mejor que el vacío para reaccionar. Parece carecer de los conocimientos básicos que se imparten a diario en nuestras escuelas secundarias». Obviamente, los escritores editoriales del New York Times de la época no vieron los conocimientos básicos que se impartían en este curso.

De hecho, como hemos discutido, la conservación del momento en una colisión se deriva de las leyes de Newton. Sin embargo, se trata de un concepto más general, más sencillo, que no depende en absoluto de los detalles de las interacciones, etc. Esta simplicidad evidentemente atrajo a Einstein, que estaba convencido de que cuando la dinámica se reformulara para incluir las nuevas ideas sobre el tiempo y el espacio, la conservación del momento debería seguir siendo válida en cualquier marco inercial. Esto le llevó a algunas conclusiones sorprendentes, como veremos.

Conservación del momento en la mesa de billar

Como ejercicio de calentamiento, consideremos la conservación del momento para una colisión de dos bolas en una mesa de billar. Trazamos una línea de tiza en el centro de la mesa de billar y lanzamos las bolas cerca de la línea de tiza, pero en lados opuestos, desde ambos extremos, a la misma velocidad, de modo que chocarán en el centro con un golpe de refilón, lo que hará que sus velocidades cambien en un pequeño ángulo. En otras palabras, si inicialmente decimos que sus velocidades (de igual magnitud y dirección opuesta) eran paralelas a la dirección x -la línea de tiza-, después de la colisión también tendrán pequeñas velocidades iguales y opuestas en la dirección y. (Las velocidades en la dirección x habrán disminuido muy ligeramente).

Una colisión simétrica de naves espaciales

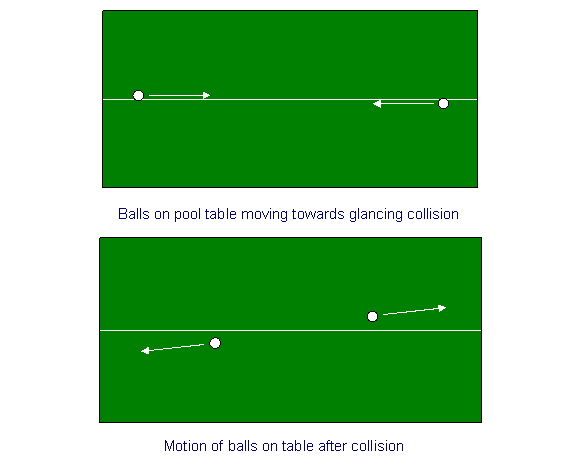
Ahora repitamos el ejercicio a gran escala. Supongamos que en algún lugar del espacio, lejos de cualquier campo gravitatorio, colocamos una cuerda de un millón de millas de largo. (Podría estar entre nuestros dos relojes en el experimento de dilatación del tiempo). Esta cuerda corresponde a la línea de tiza de la mesa de billar. Supongamos ahora que tenemos dos naves espaciales idénticas que se acercan con velocidades iguales y opuestas paralelas a la cuerda desde los dos extremos de la misma, orientadas de tal manera que sufren una ligera colisión cuando se encuentran en el centro. De la simetría de la situación se desprende que el momento se conserva en ambas direcciones. En particular, la velocidad con la que una nave espacial se aleja de la cuerda después de la colisión -su velocidad y- es igual y opuesta a la velocidad con la que la otra se aleja de la cuerda.

Pero consideremos ahora esta colisión observada por alguien en una de las naves espaciales, llamémosla A. Antes de la colisión, ve la cuerda moviéndose muy rápido por la ventana, digamos a unos pocos metros de distancia. Después de la colisión, ve que la cuerda se aleja, digamos, a 15 metros por segundo. Esto se debe a que la nave espacial Ah ha adquirido una velocidad perpendicular a la cuerda de 15 metros por segundo. Mientras tanto, dado que se trata de una situación completamente simétrica, un observador en la nave espacial B deduciría sin duda que su nave espacial se aleja de la cuerda a 15 metros por segundo también.

¿Cómo de simétrico es?

La pregunta crucial es: ¿a qué velocidad ve un observador de la nave espacial A que la nave espacial B se aleja de la cuerda? Supongamos que en relación con la nave espacial A, la nave espacial B se aleja (en la dirección x) a 0,6c. En primer lugar, recordemos que las distancias perpendiculares a la dirección del movimiento no tienen contracción de Lorentz. Por lo tanto, cuando el observador de la nave B dice que se ha alejado 15 metros de la cuerda en un intervalo de un segundo, el observador que ve este movimiento desde la nave A estará de acuerdo con los 15 metros, pero no con el segundo. El observador dirá que sus relojes van lentos, por lo que, medidos por sus relojes, habrán transcurrido 1,25 segundos mientras ella se mueve 15 metros en la dirección y.

Se deduce que, como resultado de la dilatación del tiempo, esta colisión vista desde la nave espacial A no causa velocidades iguales y opuestas para las dos naves espaciales en la dirección y. Inicialmente, ambas naves espaciales se movían en paralelo al eje x, había un impulso cero en la dirección y. Entonces, ¿cómo podemos argumentar que hay un momento total cero en la dirección y después de la colisión, cuando las naves espaciales idénticas no tienen velocidades iguales y opuestas?

Einstein rescata la conservación del momento

Einstein estaba tan seguro de que la conservación del momento debe mantenerse siempre que la rescató con una hipótesis audaz: ¡la masa de un objeto debe depender de su velocidad! De hecho, la masa debe aumentar con la velocidad de forma que se anule la menor velocidad en la dirección y resultante de la dilatación del tiempo. Es decir, si un objeto en reposo tiene una masa m, moviéndose a una velocidad v tendrá la inercia correspondiente a una «masa relativista» m rel =m/ 1-( v 2 / c 2 ) .Entonces el momento se convierte en

p → = m rel v → =m v → / 1-( v 2 / c 2 ) .

Nótese que este aumento de masa relativista es un efecto indetectablemente pequeño a velocidades ordinarias, pero a medida que un objeto se acerca a la velocidad de la luz, ¡la masa aumenta sin límite!

La masa realmente aumenta con la velocidad

¡Decidir que las masas de los objetos deben depender de la velocidad así parece un precio muy alto para rescatar la conservación del momento! Sin embargo, se trata de una predicción que no es difícil de comprobar mediante experimentos. La primera confirmación llegó en 1908, desviando electrones rápidos en un tubo de vacío. De hecho, los electrones en un tubo de colorTV de estilo antiguo tienen alrededor de medio por ciento más de inercia que los electrones en reposo, y esto debe tenerse en cuenta en el cálculo de los campos magnéticos utilizados para guiarlos a la pantalla.

Mucho más dramático, en los modernos aceleradores de partículas se utilizan campos eléctricos muy potentes para acelerar electrones, protones y otras partículas. En la práctica, se comprueba que estas partículas necesitan fuerzas cada vez mayores para seguir acelerando a medida que se aproxima la velocidad de la luz. En consecuencia, la velocidad de la luz es un límite natural de velocidad absoluta. Las partículas se aceleran a velocidades en las que su masa relativista es miles de veces mayor que su masa medida en reposo, normalmente llamada «masa en reposo».

…¿O no?

En realidad, hay un debate continuo entre los físicos sobre el concepto de masa relativista. El debate es en gran medida semántico: nadie duda de que la expresión correcta para el momento de una partícula con una masa en reposo m que se mueve con una velocidad v → es p → = m 1- v 2 / c 2 v → . Pero a los físicos de partículas en particular, muchos de los cuales se pasan la vida midiendo las masas en reposo de las partículas con gran precisión, no les gusta escribir esto como p → = m rel v → . No les gusta la idea de una masa variable. Por un lado, podría dar la impresión de que, a medida que se acelera, una partícula aumenta de tamaño, o al menos su estructura interna se altera de alguna manera. En realidad, una partícula relativista sólo sufre una contracción de Lorentz en la dirección del movimiento, como cualquier otra cosa. Pasa de una forma esférica a una forma de disco con el mismo radio transversal.

Entonces, ¿cómo puede entenderse este «aumento de masa»? Como siempre, Einstein tenía razón: señaló que toda forma de energía posee inercia. La propia energía cinética tiene inercia. Ahora bien, la «inercia» es una propiedad definitoria de la masa. La otra propiedad fundamental de la masa es que atrae gravitatoriamente. ¿Esta energía cinética hace eso? Para ver la respuesta, consideremos una esfera llena de gas. Generará un campo gravitatorio esféricamente simétrico fuera de ella, de fuerza proporcional a la masa total. Si ahora calentamos el gas, las partículas del gas tendrán este aumento de masa (relativista), correspondiente a su aumento de energía cinética, y el campo gravitatorio externo habrá aumentado proporcionalmente. (Nadie duda de esto.)

Así pues, la «masa relativista» tiene efectivamente las dos propiedades básicas de la masa: inercia y atracción gravitatoria. (Como quedará claro en las siguientes clases, esta masa relativista no es más que la energía total, con la propia masa en reposo vista ahora como energía.)

En un nivel más trivial, algunos profesores se oponen a introducir la masa relativista porque temen que los estudiantes asuman que la energía cinética de una partícula en movimiento relativista es sólo 1 2 m v → 2 utilizando la masa relativista – no es así, como veremos en breve.

Nota de pie de página: Para cualquiera que pueda pasar en algún momento a un tratamiento mortemáticamente sofisticado, hay que añadir que la masa en reposo juega un papel importante como invariante al pasar de un marco de referencia a otro, pero la «masa relativista» que se utiliza aquí es realmente sólo la primera componente (la energía) del vector energía-momento de cuatro dimensiones de una partícula, y por lo tanto no es un invariante.

Energía cinética y masa para partículas muy rápidas

Pensemos en la energía cinética de una de estas partículas que viaja cerca de la velocidad de la luz. Recordemos que en una conferencia anterior encontramos que la energía cinética de una masa m ordinaria no relativista (es decir, de movimiento lento) era de 1 2 m v 2 . La forma en que lo hicimos fue considerando cuánto trabajo tuvimos que hacer para elevarla a una cierta altura: tuvimos que ejercer una fuerza igual a su peso W para elevarla a una altura h, siendo el trabajo total realizado, o la energía gastada, la fuerza x la distancia, Wh. Al volver a caer, la fuerza de la gravedad, W, realizó exactamente la misma cantidad de trabajo Wh sobre el objeto que caía, pero esta vez el trabajo se dedicó a acelerar el objeto, para darle energía cinética. Como sabemos la velocidad que adquieren los objetos que caen, pudimos concluir que la energía cinética era de 1 2 m v 2 . (Para más detalles, véase la conferencia anterior.)

De forma más general, podríamos haber acelerado la masa con cualquier fuerza constante F, y encontrar el trabajo realizado por la fuerza (fuerza xdistancia) para conseguir que alcance la velocidad v desde un punto de partida. La energía cinética de la masa, E= 1 2 m v 2 , es exactamente igual al trabajo realizado por la fuerza para llevar la masa a esa velocidad. (Se puede demostrar de forma similar que si se aplica una fuerza a una partícula que ya se mueve a la velocidad u, digamos, y se acelera hasta la velocidad v, el trabajo necesario es 1 2 m v 2 – 1 2 m u 2 . )

Es interesante intentar repetir el ejercicio para una partícula que se mueve muy cerca de la velocidad de la luz, como las partículas en los aceleradores mencionados en el párrafo anterior. La Segunda Ley de Newton, en la forma

Fuerza = tasa de cambio de momento

sigue siendo cierta, pero cerca de la velocidad de la luz la velocidad cambia de forma insignificante mientras la fuerza sigue actuando – ¡en cambio, la masa aumenta! Por lo tanto, podemos escribir con una excelente aproximación,

Fuerza = (tasa de cambio de la masa) x c

donde como siempre c es la velocidad de la luz. Para ser más específicos, supongamos que tenemos una fuerza constante F que empuja una partícula. En algún instante, la partícula tiene una masa M, y una velocidad extremadamente cercana a c. Un segundo más tarde, dado que la fuerza sigue actuando sobre la partícula, y así aumenta su momento a partir de la Segunda Ley de Newton, la partícula tendrá una masa M+m digamos, donde m es el aumento de masa como resultado del trabajo realizado por la fuerza.

¿Cuál es el aumento de la energía cinética E de la partícula durante ese segundoperíodo? Por analogía exacta con el caso no relativista revisado anteriormente, es sólo el trabajo realizado por la fuerza durante ese período. Ahora bien, como la masa de la partícula cambia en m en un segundo, m es también la tasa de cambio de la masa. Por lo tanto, a partir de la Segunda Ley de Newton en la forma

Fuerza = (tasa de cambio de masa) x c,

podemos escribir

Fuerza =mc.

El aumento de la energía cinética E durante el período de un segundo es sólo el trabajo realizado por la fuerza,

E= fuerza x distancia.

Como la partícula se mueve esencialmente a la velocidad de la luz, la distancia sobre la que actúa la fuerza en el período de un segundo es sólo c metros, c=3× 10 8 .

Así que el trabajo total que realiza la fuerza en ese segundo es fuerza xdistancia =mc×c=m c 2 .

De ahí que la relación entre el aumento de masa de la partícula relativista y su aumento de energía cinética sea:

E=m c 2 .

Energía cinética y masa para partículas lentas

Recordemos que para que las leyes de Newton se cumplan en todos los marcos de inercia, tuvimos que suponer un aumento de la masa con la velocidad en el factor 1/ 1-( v 2 / c 2 ) . Esto implica que incluso un objeto que se mueve lentamente ¡tiene un pequeño aumento de masa cuando se mueve!

¿Cómo se relaciona ese diminuto aumento con la energía cinética? Consideremos una masa M, que se mueve a una velocidad v, mucho menor que la velocidad de la luz. Su energía cinética E= 1 2 M v 2 , como se ha comentado anteriormente. Su masa es M/ 1-( v 2 / c 2 ) , que podemos escribir como M+m. ¿Qué es m ?

Como estamos hablando de velocidades con las que estamos familiarizados, como un avión a reacción, en el que v/c, es realmente pequeño, podemos utilizar algunos trucos matemáticos sencillos para facilitar las cosas.

El primero es una buena aproximación para la raíz cuadrada de 1-x cuando x es mucho menor que uno:

1-x ≅1- 1 2 x para x≪1.

Puedes comprobarlo fácilmente con tu calculadora: prueba con x= 1 100 , encuentras que 99 100 =0,994987… que es extremadamente cercano a 1- 1 2 1 100 =0,995¡

La siguiente aproximación es

1 1-x ≅1+x para x≪1.

Esto también es fácil de comprobar: toma de nuevo x= 1 100 : 1 1-x = 1 99 100 = 100 99 =1,01010… ,y 1+x= 101 100 =1,01.

Usando estas aproximaciones con x=v/c, podemos aproximar 1-( v 2 / c 2 ) como 1- 1 2 ( v 2 / c 2 ) ,y luego 1/( 1- 1 2 ( v 2 / c 2 ) ) como 1+ 1 2 ( v 2 / c 2 ) .

Esto significa que la masa total a la velocidad v

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ),

y escribiendo esto como M+m, vemos que el aumento de masa m es igual a 1 2 M v 2 / c 2 .

Esto significa que -de nuevo- el aumento de masa m está relacionado con la energía cinética E por E=m c 2 .

De hecho, no es difícil demostrar, utilizando un poco de cálculo, que en todo el rango de velocidad desde cero hasta lo más cercano a la velocidad de la luz, una partícula en movimiento experimenta un aumento de masa relacionado con su energía cinética por E=m c 2 . Para entender por qué esto no se nota en la vida cotidiana, pruebe con un ejemplo, como un avión de 100 toneladas que se mueve a 2.000 mph. 100 toneladas son 100.000 kilogramos, 2.000 mph son unos 1.000 metros por segundo. Eso es una energía cinética 1 2 M v 2 de ½ ×1011joules, pero el correspondiente cambio de masa del avión por el factor c 2 , 9× 10 16 , dando un aumento de masa real de alrededor de medio miligramo, ¡no muy fácil de detectar!

E = mc2

Hemos visto anteriormente que cuando una fuerza realiza un trabajo acelerando un cuerpo para darle energía cinética, la masa del cuerpo aumenta en una cantidad igual al trabajo total realizado por la fuerza, la energía E transferida, dividida por c 2 . ¿Qué ocurre cuando una fuerza realiza un trabajo sobre un cuerpo que no lo acelera, por lo que no aumenta la energía cinética? Por ejemplo, ¿qué pasa si simplemente levanto algo a un ritmo constante, dándole energía potencial? Resulta que también en este caso se produce un aumento de la masa dado por E=m c 2 , por supuesto inconmensurablemente pequeño para los objetos cotidianos.

Sin embargo, este es un efecto medible e importante en la física nuclear. Por ejemplo, el átomo de helio tiene un núcleo que tiene dos protones y dos neutrones unidos muy fuertemente por una fuerza de atracción nuclear fuerte. Si se aplica una fuerza exterior suficiente, puede separarse en dos núcleos de «hidrógeno pesado», cada uno de los cuales tiene un protón y un neutrón. Hay que gastar mucha energía externa para lograr esta separación, y se descubre que la masa total de los dos núcleos de hidrógeno pesado es mediblemente (alrededor de medio punto porcentual) más pesada que el núcleo de helio original. Esta extramasa, multiplicada por c 2 , es igual a la energía necesaria para dividir el núcleo de helio en dos. Y lo que es más importante, esta energía puede recuperarse dejando que los dos hidrogeniones pesados colisionen y se unan para formar de nuevo un núcleo de helio. (Ambos están cargados eléctricamente de forma positiva, por lo que se repelen, y deben juntarse bastante rápido para superar esta repulsión y llegar a la cercanía en la que entra en juego la atracción nuclear, mucho más fuerte). Esta es la fuente de energía básica de la bomba de hidrógeno, y del sol.

Resulta que todas las formas de energía, cinética y diferentes tipos de energía potencial, tienen una masa asociada dada por E=m c 2 . Para las reacciones nucleares, el cambio de masa es típicamente del orden de una milésima de la masa total, y fácilmente medible. En el caso de las reacciones químicas, el cambio es del orden de una milmillonésima parte de la masa total, y no se puede medir actualmente.

Índice anterior