Následující definice robustní statistiky pochází z knihy P. J. Hubera Robustní statistika.
… každý statistický postup by měl mít následující žádoucí vlastnosti:
- Měl by mít přiměřeně dobrou (optimální nebo téměř optimální) účinnost při předpokládaném modelu.
- Měl by být robustní v tom smyslu, že malé odchylky od předpokladů modelu by měly zhoršit výkonnost jen nepatrně. …
- O něco větší odchylky od modelu by neměly způsobit katastrofu.
Klasická statistika se zaměřuje na první z Huberových bodů a vytváří metody, které jsou optimální při splnění určitých kritérií. Tento příspěvek se zabývá kanonickými příklady, které se používají k ilustraci druhého a třetího Huberova bodu.
Třetí Huberův bod se obvykle ilustruje výběrovým průměrem (average) a výběrovým mediánem (middle value). Téměř polovinu dat ve vzorku můžete nastavit na ∞, aniž by se výběrový medián stal nekonečným. Naproti tomu výběrový průměr se stane nekonečným, pokud je jakákoli hodnota vzorku nekonečná. Velké odchylky od modelu, tj. několik odlehlých hodnot, mohou způsobit katastrofu pro výběrový průměr, ale ne pro výběrový medián.
Kanonický příklad při diskusi o druhém Huberově bodu se vrací k Johnu Tukeymu. Začněme nejjednodušším učebnicovým příkladem odhadu: data z normálního rozdělení s neznámým průměrem a rozptylem 1, tj. data jsou normální(μ, 1) s neznámým μ. Nejefektivnějším způsobem odhadu μ je vzít výběrový průměr, tedy průměr dat.
Nyní však předpokládejme, že rozdělení dat není přesně normální(μ, 1), ale že je směsí standardního normálního rozdělení a normálního rozdělení s odlišným rozptylem. Nechť δ je malé číslo, řekněme 0,01, a předpokládejme, že data pocházejí z normálního(μ, 1) rozdělení s pravděpodobností 1-δ a data pocházejí z normálního(μ, σ2) rozdělení s pravděpodobností δ. Toto rozdělení se nazývá „kontaminované normální“ a číslo δ je velikost kontaminace. Důvodem použití modelu kontaminovaného normálního rozdělení je to, že se jedná o nenormální rozdělení, které může na první pohled vypadat normálně.
Populační průměr μ bychom mohli odhadnout buď pomocí výběrového průměru, nebo výběrového mediánu. Pokud by data byla striktně normální, a nikoliv směsná, výběrový průměr by byl nejefektivnějším odhadem μ. V takovém případě by standardní chyba byla asi o 25 % větší, pokud bychom použili výběrový medián. Pokud však data pocházejí ze směsi, může být výběrový medián efektivnější, v závislosti na velikostech δ a σ. Zde je graf ARE (asymptotické relativní efektivnosti) výběrového mediánu ve srovnání s výběrovým průměrem jako funkce σ, když δ = 0.01.
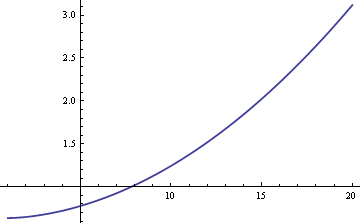
Z grafu vyplývá, že pro hodnoty σ větší než 8 je výběrový medián efektivnější než výběrový průměr. Relativní nadřazenost mediánu roste bez omezení s rostoucí hodnotou σ.
Tady je graf ARE s hodnotou σ pevně stanovenou na 10 a δ měnící se v rozmezí 0 až 1.
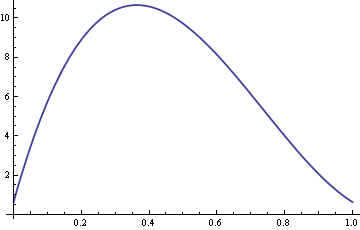
Také pro hodnoty δ kolem 0. V tomto grafu je vidět, že medián je efektivnější než průměr.4 je výběrový medián více než desetkrát efektivnější než výběrový průměr.
Obecný vzorec pro ARE v tomto příkladu je 2((1 + δ(σ2 – 1)(1 – δ + δ/σ)2)/ π.
Jste-li si jisti, že vaše data jsou normální bez kontaminace nebo s velmi malou kontaminací, pak je výběrový průměr nejúčinnějším odhadem. Může se však vyplatit riskovat, že se vzdáte malé efektivity výměnou za vědomí, že v případě výrazné kontaminace dosáhnete lepších výsledků s robustním modelem. Existuje větší potenciál ztráty při použití výběrového průměru, pokud je kontaminace významná, než potenciální zisk při použití výběrového průměru, pokud kontaminace není.
Tady je hádanka spojená s příkladem kontaminovaného normálu. Nejefektivnějším odhadem pro normální(μ, 1) data je výběrový průměr. A nejefektivnějším odhadem pro data normal(μ, σ2) je také vzít výběrový průměr. Proč tedy není optimální vzít výběrový průměr směsi?“
Klíčové je, že nevíme, zda konkrétní vzorek pochází z normálního(μ, 1) rozdělení nebo z normálního(μ, σ2) rozdělení. Kdybychom to věděli, mohli bychom vzorky oddělit, zprůměrovat je zvlášť a vzorky spojit do souhrnného průměru: jeden průměr vynásobit 1-δ, druhý vynásobit δ a sečíst. Protože však nevíme, které složky směsi vedou ke kterým vzorkům, nemůžeme vzorky vhodně zvážit. (Pravděpodobně neznáme ani δ, ale to je jiná věc.)
Existují i jiné možnosti než použití výběrového průměru nebo výběrového mediánu. Například ořezaný průměr vyhodí některé největší a nejmenší hodnoty a pak vše ostatní zprůměruje. (Někdy takto fungují sporty, kde se vyhazují nejvyšší a nejnižší známky sportovce od rozhodčích). Čím více údajů se na obou koncích vyhodí, tím více se oříznutý průměr chová jako výběrový medián. Čím méně dat se vyhodí, tím více se chová jako výběrový průměr.
Související příspěvek:
Pro každodenní tipy z oblasti datové vědy sledujte @DataSciFact na Twitteru.
.