Alai

Od Raymonda Yuana, Stážista softwarového inženýrství

V tomto tutoriálu se naučíme, jak pomocí hlubokého učení skládat obrazy ve stylu jiného obrazu (přáli jste si někdy malovat jako Picasso nebo Van Gogh?). Tomuto postupu se říká neuronový přenos stylu! Tato technika je popsána v článku Leona A. Gatyse A Neural Algorithm of Artistic Style (Neuronový algoritmus uměleckého stylu), který je skvělým čtením a určitě byste si ho měli přečíst.

Neuronový přenos stylu je optimalizační technika, která se používá k tomu, aby se vzaly tři obrázky, obsahový obrázek, referenční obrázek stylu (například umělecké dílo slavného malíře) a vstupní obrázek, který chcete stylizovat – a smíchaly se dohromady tak, že vstupní obrázek se transformuje, aby vypadal jako obsahový obrázek, ale „namalovaný“ ve stylu stylového obrázku.

Příklad vezměme obrázek této želvy a obraz Velké vlny u Kanagawy od Katsushiky Hokusaie:

Jak by to vypadalo, kdyby se Hokusai rozhodl přidat do obrazu želvy texturu nebo styl svých vln? Něco takového?“

Je to magie nebo jen hluboké učení? Naštěstí se nejedná o žádnou magii: přenos stylu je zábavná a zajímavá technika, která ukazuje schopnosti a vnitřní reprezentaci neuronových sítí.

Princip neuronového přenosu stylu spočívá v definování dvou funkcí vzdálenosti, jedné, která popisuje, jak rozdílný je obsah dvou obrázků, Lcontent, a druhé, která popisuje rozdíl mezi oběma obrázky z hlediska jejich stylu, Lstyle. Pak se při zadání tří obrázků, požadovaného obrázku stylu, požadovaného obrázku obsahu a vstupního obrázku (inicializovaného obrázkem obsahu), pokusíme transformovat vstupní obrázek tak, abychom minimalizovali vzdálenost obsahu s obrázkem obsahu a jeho vzdálenost stylu s obrázkem stylu.

Shrnem vezmeme základní vstupní obrázek, obrázek obsahu, který chceme porovnat, a obrázek stylu, který chceme porovnat. Základní vstupní obrázek transformujeme minimalizací vzdáleností (ztrát) obsahu a stylu pomocí zpětného šíření a vytvoříme obrázek, který odpovídá obsahu obrázku obsahu a stylu obrázku stylu.

Při tomto postupu získáme praktické zkušenosti a rozvineme intuici ohledně následujících pojmů:

• Eager Execution – využijeme imperativní programovací prostředí TensorFlow, které vyhodnocuje operace okamžitě
• Zjistíme více o eager execution
• Podíváme se na něj v akci (mnoho tutoriálů je možné spustit v Colaboratory)
• Použití funkčního API k definici modelu – vytvoříme podmnožinu našeho modelu, která nám poskytne přístup k potřebnému mezilehlé aktivace pomocí funkčního rozhraní API
• Využití map příznaků předtrénovaného modelu – naučíme se používat předtrénované modely a jejich mapy příznaků
• Vytvoření vlastních trénovacích smyček – prozkoumáme, jak nastavit optimalizátor pro minimalizaci dané ztráty vzhledem ke vstupním parametrům

Budeme postupovat podle obecných kroků pro provedení přenosu stylu:

1. Vizualizace dat
2. Základní předzpracování/příprava našich dat
3. Nastavení ztrátové funkce
4. Vytvoření modelu
5. Optimalizace pro ztrátovou funkci

Posluchači: Tento příspěvek je určen pro středně pokročilé uživatele, kteří ovládají základní koncepty strojového učení. Abyste si z tohoto příspěvku odnesli co nejvíce, měli byste:

• Přečíst si Gatysův článek – vysvětlíme vám to průběžně, ale článek vám poskytne důkladnější pochopení úlohy
• Pochopit gradientní sestup

Odhadovaný čas: 60 min

Kód:

Kompletní kód tohoto článku najdete na tomto odkazu. Pokud si chcete tento příklad projít krok za krokem, najdete kolab zde.

Implementace

Začneme tím, že povolíme eager execution. Eager execution nám umožní pracovat s touto technikou co nejpřehledněji a nejčitelněji.

Definice reprezentace obsahu a stylu

Abychom získali reprezentaci obsahu i stylu našeho obrázku, podíváme se na některé mezivrstvy v rámci našeho modelu. Mezivrstvy představují mapy prvků, které jsou s postupující hloubkou stále lépe uspořádané. V tomto případě používáme síťovou architekturu VGG19, předtrénovanou síť pro klasifikaci obrazu. Tyto mezivrstvy jsou nezbytné k definování reprezentace obsahu a stylu z našich obrázků. Pro vstupní obrázek se pokusíme v těchto mezivrstvách přiřadit odpovídající cílové reprezentace stylu a obsahu.

Proč mezivrstvy?

Možná se ptáte, proč nám tyto mezivrstvy v rámci naší předtrénované sítě pro klasifikaci obrázků umožňují definovat reprezentace stylu a obsahu. Na vysoké úrovni lze tento jev vysvětlit tím, že aby síť mohla provádět klasifikaci obrazu (k čemuž byla naše síť vyškolena), musí obrazu rozumět. To zahrnuje přijetí surového obrazu jako vstupních pixelů a vytvoření vnitřní reprezentace prostřednictvím transformací, které přemění surové pixely obrazu na komplexní porozumění rysům přítomným v obraze. To je také částečně důvod, proč jsou konvoluční neuronové sítě schopny dobře zobecňovat: jsou schopny zachytit invarianty a definující rysy v rámci tříd (např. kočky vs. psi), které jsou agnostické vůči šumu na pozadí a dalším rušivým vlivům. Tedy někde mezi místem, kam se přivádí surový obrázek, a výstupem klasifikační značky slouží model jako komplexní extraktor příznaků; proto jsme pomocí přístupu k mezivrstvám schopni popsat obsah a styl vstupních obrázků.

Konkrétně z naší sítě vytáhneme tyto mezivrstvy:

Model

V tomto případě načteme VGG19 a do modelu přivedeme náš vstupní tenzor. To nám umožní extrahovat mapy příznaků (a následně reprezentace obsahu a stylu) obsahu, stylu a generovaných obrázků.

Použijeme VGG19, jak je navrženo v článku. Navíc vzhledem k tomu, že VGG19 je poměrně jednoduchý model (ve srovnání s ResNetem, Inceptionem atd.), mapy rysů ve skutečnosti fungují lépe pro přenos stylu.

Pro přístup k mezivrstvám odpovídajícím našim mapám rysů stylu a obsahu získáme odpovídající výstupy pomocí rozhraní Keras Functional API k definování našeho modelu s požadovanými výstupními aktivacemi.

Pomocí rozhraní Functional API definování modelu jednoduše zahrnuje definování vstupu a výstupu: model = Model(inputs, outputs).

V uvedeném úryvku kódu načteme naši předtrénovanou síť pro klasifikaci obrázků. Poté uchopíme zájmové vrstvy, jak jsme je definovali dříve. Poté definujeme Model tak, že nastavíme vstupy modelu na obrázek a výstupy na výstupy vrstev stylu a obsahu. Jinými slovy, vytvořili jsme model, který přijme vstupní obrázek a výstupy mezivrstev obsahu a stylu!

Definice a vytvoření našich ztrátových funkcí (vzdálenosti obsahu a stylu)

Naše definice ztrát obsahu je vlastně docela jednoduchá. Síti předáme jak požadovaný obsahový obrázek, tak náš základní vstupní obrázek. Tím se z našeho modelu vrátí výstupy mezivrstev (z vrstev definovaných výše). Pak jednoduše vezmeme euklidovskou vzdálenost mezi oběma mezilehlými reprezentacemi těchto obrázků.

Formálněji řečeno, ztráta obsahu je funkce, která popisuje vzdálenost obsahu od našeho vstupního obrázku x a našeho obsahového obrázku, p . Nechť Cₙₙ je předtrénovaná hluboká konvoluční neuronová síť. V tomto případě opět použijeme VGG19. Nechť X je libovolný obrázek, pak Cₙₙ(x) je síť napájená obrázkem X. Nechť Fˡᵢⱼ(x)∈ Cₙₙ(x)a Pˡᵢⱼ(x) ∈ Cₙₙ(x) popisují příslušnou mezilehlou reprezentaci funkcí sítě se vstupy x a p ve vrstvě l . Obsahovou vzdálenost (ztrátu) pak formálně popíšeme takto:

Zpětné šíření provedeme obvyklým způsobem tak, abychom tuto obsahovou ztrátu minimalizovali. Měníme tedy výchozí obrázek tak dlouho, dokud v určité vrstvě (definované v content_layer) nevytvoří podobnou odezvu jako původní obsahový obrázek.

Tento postup lze realizovat poměrně jednoduše. Opět bude jako vstup brát mapy příznaků ve vrstvě L v síti napájené x, naším vstupním obrázkem, a p, naším obrázkem obsahu, a vrátí vzdálenost obsahu.

Ztráta stylu:

Výpočet ztráty stylu je trochu složitější, ale probíhá na stejném principu, tentokrát naší síti dodáme základní vstupní obrázek a obrázek stylu. Místo porovnávání surových mezivýstupů základního vstupního obrázku a obrázku stylu však místo toho porovnáváme Gramovy matice obou výstupů.

Matematicky popisujeme ztrátu stylu základního vstupního obrázku x a obrázku stylu a jako vzdálenost mezi reprezentací stylu (Gramovými maticemi) těchto obrázků. Reprezentaci stylu obrazu popisujeme jako korelaci mezi různými odezvami filtru danou Gramovou maticí Gˡ, kde Gˡᵢⱼ je vnitřní součin mezi vektorizovanou mapou příznaků i a j ve vrstvě l. Vidíme, že Gˡᵢⱼ vytvořený nad mapou příznaků pro daný obrázek představuje korelaci mezi mapami příznaků i a j.

Pro vytvoření stylu pro náš základní vstupní obrázek provedeme gradientní sestup z obsahového obrázku, abychom jej transformovali na obrázek, který odpovídá reprezentaci stylu původního obrázku. Učiníme tak minimalizací střední kvadratické vzdálenosti mezi korelační mapou příznaků obrazu stylu a vstupním obrazem. Příspěvek každé vrstvy k celkové ztrátě stylu je popsán vztahem

kde Gˡᵢⱼ a Aˡᵢⱼ jsou příslušné reprezentace stylu ve vrstvě l vstupního obrazu x a obrazu stylu a. Nl popisuje počet map prvků, z nichž každá má velikost Ml=výška∗šířka. Celková ztráta stylu v každé vrstvě je tedy

kde příspěvek ztráty každé vrstvy vážíme určitým faktorem wl. V našem případě vážíme každou vrstvu stejně:

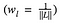
Toto se realizuje jednoduše:

Spustit gradientní sestup

Pokud nejste obeznámeni s gradientním sestupem/zpětným šířením nebo si ho potřebujete osvěžit, určitě se podívejte na tento zdroj.

V tomto případě použijeme optimalizátor Adam, abychom minimalizovali ztrátu. Iterativně aktualizujeme náš výstupní obraz tak, aby minimalizoval naši ztrátu: neaktualizujeme váhy spojené s naší sítí, ale místo toho trénujeme náš vstupní obraz tak, aby minimalizoval ztrátu. Abychom to mohli provést, musíme vědět, jak vypočítáme naši ztrátu a gradienty. Všimněte si, že optimalizátor L-BFGS, který, pokud tento algoritmus znáte, doporučujeme, ale v tomto tutoriálu není použit, protože hlavní motivací tohoto tutoriálu bylo ilustrovat osvědčené postupy s nedočkavým prováděním. Pomocí Adama můžeme demonstrovat funkčnost autograd/gradientní pásky s vlastními tréninkovými smyčkami.

Výpočet ztráty a gradientů

Definujeme malou pomocnou funkci, která načte náš obrázek obsahu a stylu, předá je naší síti, která pak z našeho modelu vypíše reprezentace prvků obsahu a stylu.

Pro výpočet gradientu použijeme tf.GradientTape. Umožňuje nám využít automatickou diferenciaci, která je k dispozici při trasovacích operacích pro pozdější výpočet gradientu. Zaznamenává operace během dopředného průchodu a poté je schopen vypočítat gradient naší ztrátové funkce vzhledem k našemu vstupnímu obrázku pro zpětný průchod.

Poté je výpočet gradientů snadný:

Použijeme a spustíme proces přenosu stylu

A abychom skutečně provedli přenos stylu:

A je to!

Spustíme jej na našem obrázku želvy a Hokusaiově Velké vlně u Kanagawy:

Sledujte iterační proces v čase:

Tady jsou další skvělé příklady toho, co dokáže přenos neuronového stylu. Podívejte se na to!

Vyzkoušejte si vlastní obrázky!

Co jsme probrali:

• Sestavili jsme několik různých ztrátových funkcí a pomocí zpětného šíření jsme transformovali náš vstupní obrázek tak, abychom tyto ztráty minimalizovali.
• Za tímto účelem jsme načetli předtrénovaný model a použili jeho naučené mapy příznaků k popisu reprezentace obsahu a stylu našich obrázků.
• Naší hlavní ztrátovou funkcí byl především výpočet vzdálenosti z hlediska těchto různých reprezentací.
• To jsme implementovali pomocí vlastního modelu a dychtivého provádění.
• Náš vlastní model jsme vytvořili pomocí Functional API.
• Eager execution nám umožňuje dynamicky pracovat s tenzory pomocí přirozeného toku řízení jazyka Python.
• Manipulovali jsme přímo s tenzory, což usnadňuje ladění a práci s tenzory.

Iterativně jsme aktualizovali náš obraz použitím pravidel aktualizace našich optimalizátorů pomocí tf.gradient. Optimalizátor minimalizoval dané ztráty vzhledem k našemu vstupnímu obrazu.