Alai

Michael Fowler,UVa Physics.

Momentum má Směr

Jak jsme probírali v minulé přednášce, ještě předtím, než Newton formuloval své zákony, Descartes s malou pomocí Huygense objevil hlubokoudynamickou pravdu: při jakékoli srážce nebo vlastně při jakékoli interakci jakéhokoli druhu zůstává celkové množství „hybnosti“ – míry pohybu – vždy stejné. Hybnost pohybujícího se objektu je definována jako součin hmotnosti a rychlosti, a je tedy vektorem: má velikost a směr. Pokud stojíte na bruslích bez tření a hodíte míč, pohybujete se dozadu: máte moment hybnosti, který má stejnou velikost, ale opačný směr než míč, takže celková hybnost (vaše plus míčova) zůstává nulová. Stejným způsobem fungují rakety, které vymršťují materiál vysokou rychlostí. Nefungují tak, že „tlačí proti vzduchu“, ale tak, že tlačí proti materiálu, který vytlačují, stejně jako vy tlačíte proti balonu, který vrháte, a ten vás tlačí zpět, což způsobuje vaše zrychlení.

Pokud se stále domníváte, že rakety skutečně tlačí proti vzduchu, nezapomeňte, že stejně dobře fungují i ve vesmíru! Ve skutečnosti se všeobecně věřilo, že když Goddard, první americký rakeťák (je po něm pojmenováno Goddard Space Flight Center), mluvil o raketách ve vesmíru, ztrácel čas. Citujme z úvodníku New York Times z roku 1921: „Profesor Goddard nezná vztah mezi akcí a reakcí a potřebu mít něco lepšího než vakuum, proti čemu lze reagovat. Zdá se, že mu chybí základní znalosti, které se denně přednášejí na našich středních školách.“ Je zřejmé, že tehdejší redaktoři New York Times si základních znalostí, které se v tomto kurzu přednášejí, nevšimli!

Ve skutečnosti, jak jsme si řekli, vyplývá zachování hybnosti při srážce z Newtonových zákonů. Je to však obecnější, jednodušší koncept – vůbec nezávisí na detailech interakcí atd. Tato jednoduchost se zřejmě zalíbila Einsteinovi, který byl přesvědčen, že když byla dynamika přeformulována tak, aby zahrnovala nové představy o čase a prostoru, mělo by zachování hybnosti stále platit v jakékoli inerciální soustavě. To ho vedlo k některým překvapivým závěrům, jak uvidíme.

Zachování hybnosti na kulečníkovém stole

Jako cvičení na zahřátí uvažujme zachování hybnosti pro srážku dvou koulí na kulečníkovém stole. Nakreslíme křídou čáru uprostřed kulečníkového stolu a vystřelíme koule blízko křídy, ale na opačných stranách křídy z obou konců, stejnou rychlostí, takže se srazí uprostřed šikmým úderem, který otočí jejich rychlosti o malý úhel. Jinými slovy, pokud jsme původně řekli, že jejich (stejně velké, opačného směru) rychlosti byly rovnoběžné se směrem x – chalkline – pak po srážce budou mít také stejné a opačné malé rychlosti ve směru y. (Rychlosti ve směru x se velmi mírně sníží).

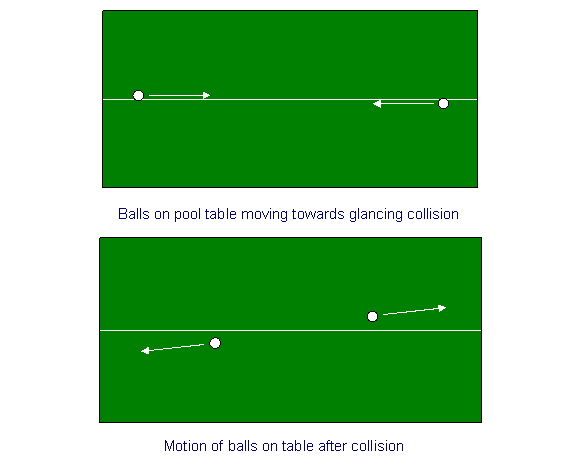
Symetrická srážka kosmických lodí

Zopakujme si nyní cvičení ve velkém měřítku. Předpokládejme, že někde ve vesmíru, daleko od jakýchkoligravitačních polí, rozestavíme strunu dlouhou jeden milion mil. (Mohla by být mezi našimi dvěma hodinami v experimentu s dilatací času). Tato struna odpovídá křídové čáře na kulečníkovém stole. Předpokládejme, že nyní máme dvě identické kosmické lodě, které se k sobě blíží stejnou a opačnou rychlostí rovnoběžně s touto strunou z obou konců struny a jsou nasměrovány tak, že při setkání uprostřed struny dojde k jejich mírné srážce. Ze symetrie situace je zřejmé, že hybnost se zachovává v obou směrech. Zejména rychlost, kterou se jedna loď po srážce vzdaluje od struny – její rychlost y – je stejná a opačná k rychlosti, kterou se od struny vzdaluje druhá loď.

Ale nyní uvažujme tuto srážku, jak ji pozoruje někdo v jedné z kosmických lodí, nazvěme ji A. Před srážkou vidí, že se struna pohybuje velmi rychle u okna, řekněme několik metrů daleko. Po srážce vidí, že se struna vzdaluje, řekněme rychlostí 15 metrů za sekundu. Je to proto, že kosmická loď Ahnabrala rychlost kolmou k provázku 15 metrů za sekundu. Protože se jedná o zcela symetrickou situaci, pozorovatel na lodi B by jistě usoudil, že se její loď také vzdaluje od struny rychlostí 15 metrů za sekundu.

Jak moc je to symetrické?

Klíčová otázka zní: jak rychle se podle pozorovatele z kosmické lodi A vzdaluje kosmická loď B od struny? Předpokládejme, že vzhledem k kosmické lodi A se kosmická loď B vzdaluje (ve směru x) rychlostí 0,6c. Nejprve si připomeňme, že vzdálenosti kolmé ke směru pohybu nejsou Lorentzovou kontrakcí. Proto když pozorovatel v kosmické lodi B řekne, že se od struny vzdálila o 15 metrů v intervalu jedné sekundy, pozorovatel sledující tento pohyb z kosmické lodi A bude souhlasit s 15 metry – ale nebude souhlasit s jednou sekundou! Řekne, že její hodiny běží pomalu, takže měřeno jeho hodinami uplyne 1,25 sekundy, když se posunula o 15 metrů ve směru y .

Z toho vyplývá, že v důsledku dilatace času tato srážka při pohledu z kosmické lodi A nezpůsobí stejnou a opačnou rychlost obou kosmických lodí ve směru y. Z toho vyplývá, že tato srážka bude mít za následek stejnou a opačnou rychlost. Zpočátku se obě kosmické lodě pohybovaly rovnoběžně s osou x, ve směru y existoval nulový moment hybnosti. Jak tedy můžeme tvrdit, že po srážce je ve směru y nulová celková hybnost, když shodné kosmické lodě nemají stejné a opačné rychlosti?

Einstein zachraňuje zachování hybnosti

Einstein si byl tak jistý, že zachování hybnosti musí vždy platit, že ho zachránil odvážnou hypotézou: hmotnost objektu musí záviset na jeho rychlosti! Ve skutečnosti musí hmotnost s rychlostí růst právě takovým způsobem, aby se zrušila nižší rychlost ve směru y, která je důsledkem dilatace času. To znamená, že má-li objekt v klidu hmotnost m, pohybuje-li se rychlostí v, bude mít setrvačnost odpovídající „relativistické hmotnosti“ m rel =m/ 1-( v 2 / c 2 ) . pak hybnost nabývá hodnoty

p → = m rel v → =m v → / 1-( v 2 / c 2 ) .

Všimněte si, že tento relativistický nárůst hmotnosti je při běžných rychlostech neznatelně malý, ale jak se objekt blíží rychlosti letu, hmotnost se neomezeně zvyšuje!

Hmotnost skutečně roste s rychlostí

Rozhodnutí, že hmotnosti objektů musí záviset na rychlosti, se zdá být vysokou cenou za záchranu zachování hybnosti! Je to však předpověď, kterou neníobtížné ověřit experimentem. První potvrzení přišlo v roce 1908 při vychylování rychlých elektronů ve vakuové trubici. Ve skutečnosti mají elektrony ve starém typu barevné televizní trubice asi o půl procenta větší setrvačnost než elektrony v klidu, což je třeba zohlednit při výpočtu magnetických polí používaných k jejich vedení na obrazovku.

Daleko dramatičtější je, že v moderních urychlovačích částic se k urychlování elektronů, protonů a dalších částic používají velmi silná elektrická pole. V praxi se zjistilo, že tyto částice potřebují k dalšímu urychlení stále větší síly, jak se blíží rychlosti světla. V důsledku toho je rychlost světla přirozenou absolutní hranicí rychlosti. Částice jsou urychlovány na rychlosti, při nichž je jejich relativistická hmotnost tisíckrát větší než jejich hmotnost měřená v klidu, obvykle nazývaná „klidová hmotnost“.

…Nebo snad ano?

Ve skutečnosti se mezi fyziky stále diskutuje o tomto pojmu relativistické hmotnosti. Debata je z velké části sémantická: nikdo nepochybuje o tom, že správnývýraz pro hybnost částice s klidovou hmotností m pohybující se rychlostí v → je p → = m 1- v 2 / c 2 v → . Ale zejména částicoví fyzici, z nichž mnozí tráví život měřením klidových hmotností částic s velkou přesností, nejsou nadšeni z toho, že se to zapisuje jako p → = m rel v → . Nelíbí se jim představa proměnné hmotnosti. Za prvé by to mohlo vyvolat dojem, že se částice při zrychlování zvětšuje, nebo se alespoň nějak mění její vnitřní struktura. Ve skutečnosti relativistická částice pouze podléhá Lorentzově kontrakci podél směru pohybu, stejně jako cokoli jiného. Z kulového tvaru přechází na tvar podobný disku, který má stejný příčný poloměr.

Jak lze tedy toto „zvětšení hmotnosti“ chápat? Jako obvykle měl Einstein pravdu: poznamenal, že každá forma energie má setrvačnost. Samotná kinetická energie má setrvačnost. Nyní je „setrvačnost“ definující vlastností hmoty. Další základní vlastností hmoty je, že se gravitačně přitahuje. Dělá to tato kinetická energie? Chcete-li znát odpověď, uvažujte o kouli naplněné plynem. Ta bude mimo sebe vytvářet sféricky symetrické gravitační pole o síle úměrné celkové hmotnosti. Pokud nyní plyn zahřejeme, částice plynu budou mít tuto zvýšenou (relativistickou) hmotnost odpovídající jejich zvýšené kinetické energii a vnější gravitační pole se úměrně tomu zvýší. (O obojím nikdo nepochybuje.)

„Relativistická hmota“ má tedy skutečně dvě základní vlastnosti hmoty: setrvačnost a gravitační přitažlivost. (Jak se ukáže v následujících přednáškách, tato relativistická hmotnost není nic jiného než celková energie,přičemž samotná klidová hmotnost je nyní považována za energii.)

Na triviálnější úrovni mají někteří učitelé námitky proti zaváděnírelativistické hmotnosti, protože se obávají, že studenti budou předpokládat, že kinetická energie relativisticky se pohybující částice je právě 1 2 m v → 2 pomocí relativistické hmotnosti – není tomu tak, jak brzy uvidíme.

Poznámka pod čarou: Pro všechny, kteří by někdy mohli přejít k matematicky propracovanějšímu pojednání, je třeba dodat, že klidová hmotnost hraje důležitou roli jako neměnná veličina při přechodu z jednoho vztažného rámce do druhého, ale zde použitá „relativistická hmotnost“ je ve skutečnosti jen první složka (energie) čtyřrozměrného vektoru energie a hybnosti částice, a není tedy invariantem.

Kinetická energie a hmotnost pro velmi rychlé částice

Přemýšlejme o kinetické energii jedné z těchtočástic, která se pohybuje rychlostí blízkou rychlosti světla. Vzpomeňte si, že v jedné z předchozích přednášek jsme zjistili, že kinetická energie obyčejné nerelativistické (tj. pomalu se pohybující) částice m je 1 2 m v 2 . Způsob, jakým jsme to zjistili, spočíval v úvaze, jak velkou práci jsme museli vykonat, abychom ji zvedli do určité výšky: abychom ji zvedli do výšky h, museli jsme vyvinout sílu rovnající se její hmotnosti W, přičemž celková vykonaná práce neboli vynaložená energie je síla x vzdálenost, Wh. Když padal zpět dolů, gravitační síla W vykonala na padající předmět přesně stejnou práci Wh, ale tentokrát se práce vynaložila na urychlení předmětu, aby mu dodala kinetickou energii. Protože víme, jak rychle padající předměty nabírají rychlost, mohli jsme dojít k závěru, že kinetická energie byla 1 2 m v 2 . (Podrobnosti naleznete v předchozí přednášce.)

Obecněji řečeno, mohli jsme urychlit těleso libovolnoukonstantní silou F a zjistit práci vykonanou silou (síla xvzdálenost), aby se z klidového startu dostalo na rychlost v . Kinetická energie tělesa, E= 1 2 m v 2 , je přesně rovna práci vykonané silou při uvedení tělesa na tuto rychlost. (Podobným způsobem lze ukázat, že působí-li síla na částice, které se již pohybují řekněme rychlostí u, a urychlují se na rychlost v, je potřebná práce 1 2 m v 2 – 1 2 m u 2 . )

Zajímavé je zkusit zopakovat cvičení pro částici pohybující se velmi blízko rychlosti světla, jako částice v urychlovačích zmíněných v předchozím odstavci. Druhý Newtonův zákon ve tvaru

Síla = rychlostzměny hybnosti

stále platí, ale v blízkosti rychlosti světla se rychlostzmění zanedbatelně, protože síla stále působí – místo toho se hmotnost zvětšuje! Proto můžeme s výbornou aproximací napsat:

Síla = (rychlostzměnyhmotnosti) x c

kde c je jako obvykle rychlost světla. Abychom byli konkrétnější, předpokládejme, že máme konstantní sílu F, která tlačí částici. V určitém okamžiku má částice hmotnost M a rychlost extrémně blízkou c. O vteřinu později, protože síla na částici nadále působí, a tím zvyšuje její hybnost podle druhého Newtonova zákona, bude mít částice hmotnost řekněme M+m, kde m je nárůst hmotnosti v důsledku působení síly.

Jaký je přírůstek kinetické energie E částice během této jedné sekundy? Podle přesné analogie s výše uvedeným nerelativistickým případem je to právě práce vykonaná silou během této periody. Jelikož se hmotnost částice za jednu sekundu změní o m, je m také rychlost změny hmotnosti. Proto z druhého Newtonova zákona ve tvaru

Síla = (rychlost změny hmotnosti) x c,

můžeme psát

Síla =mc.

Přírůstek kinetické energie E za dobu jedné sekundy je právě práce vykonaná silou,

E= síla x vzdálenost.

Protože se částice pohybuje v podstatě rychlostí letu, vzdálenost, na kterou síla působí za dobu jedné sekundy, je právě c metrů, c=3× 10 8 .

Takže celková práce, kterou síla vykoná za tuto sekundu, je síla x vzdálenost =mc×c=m c 2 .

Z toho vyplývá, že vztah mezi nárůstem hmotnosti terestrické částice a nárůstem její kinetické energie je:

E=m c 2 .

Kinetická energie a hmotnost pro pomalé částice

Připomeňme si, že aby Newtonovy zákony platily ve všech inerciálních rámcích, museli jsme předpokládat nárůst hmotnosti s rychlostí o faktor 1/ 1-( v 2 / c 2 ) . Z toho vyplývá, že i pomalu se pohybující objektmá při pohybu nepatrný přírůstek hmotnosti!

Jak tento nepatrný nárůst souvisí s kinetickou energií? Uvažujme hmotnost M, která se pohybuje rychlostí v, mnohem menší než rychlost světla. Její kinetická energie E= 1 2 M v 2 , jak bylo uvedeno výše. Její hmotnost je M/ 1-( v 2 / c 2 ), což můžeme zapsat jako M+m. Kolik je m ?

Protože mluvíme o rychlostech, které známe, například o proudovém letadle, kde v/c, je opravdu malé, můžeme použít několik jednoduchýchmatematických triků, které nám usnadní práci.

První z nich je dobrá aproximace pro odmocninu z 1-x, když je x mnohem menší než jedna:

1-x ≅1- 1 2 x pro x≪1.

To si můžete snadno ověřit na kalkulačce: zkuste x= 1 100 , zjistíte 99 100 =0,994987… což je nesmírně blízko 1- 1 2 1 100 =0,995 !

Další aproximace je

1 1-x ≅1+x pro x≪1.

To lze také snadno ověřit: opět vezmeme x= 1 100 : 1 1-x = 1 99 100 = 100 99 =1,01010… ,a 1+x= 101 100 =1,01.

Při použití těchto aproximací s x=v/c můžeme aproximovat 1-( v 2 / c 2 ) jako 1- 1 2 ( v 2 / c 2 ) , a pak 1/( 1- 1 2 ( v 2 / c 2 ) ) jako 1+ 1 2 ( v 2 / c 2 ) .

To znamená, že celková hmotnost při rychlosti v

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ),

a když to zapíšeme jako M+m, vidíme, že přírůstek hmotnosti m se rovná 1 2 M v 2 / c 2 .

To znamená, že – opět – přírůstek hmotnosti m souvisí s kinetickou energií E vztahem E = m c 2 .

Ve skutečnosti není těžké pomocí malého kalkulu ukázat, že v celém rozsahu rychlostí od nuly až po rychlost blízkou rychlosti světla dochází u pohybující se částice k nárůstu hmotnosti, který souvisí s její kinetickou energií E=m c 2 . Abyste pochopili, proč si toho v běžném životě nevšimneme, zkuste si uvést příklad, například tryskové letadlo o hmotnosti 100 tun pohybující se rychlostí 2 000 km/h. 100 tun je 100 000 kilogramů, 2 000 km/h je přibližně 1 000 metrů za sekundu. To je akinetická energie 1 2 M v 2 o velikosti ½ ×1011joulu, ale odpovídající změna hmotnosti letadla se sníží o faktor c 2 , 9× 10 16 , což dává skutečný nárůst hmotnosti asi o půl miligramu, což není příliš snadné zjistit!

E = mc2

Výše jsme viděli, že když síla vykoná práci urychlující těleso a dodá mu kinetickou energii, hmotnost tělesa se zvětší o množství, které se rovná celkové práci vykonané silou, tedy předané energii E, děleno c 2 . A co když síla vykoná práci na tělese, které ho nezrychluje, takže nedojde ke zvýšení kinetické energie? Co když například jen něco zvedám ustálenou rychlostí, čímž mu předávám potenciální energii? Ukazuje se, že i v tomto případě dochází k nárůstu hmotnosti danému vztahem E=m c 2 , který je ovšem pro běžná tělesa neměřitelně malý.

Je to však měřitelný a důležitý efekt vjaderné fyzice. Například atom helia má jádro, které má dva protony a dva neutrony velmi těsně spojené silnou jadernou přitažlivou silou. Pokud na něj působí dostatečná vnější síla, může se rozdělit na dvě jádra „těžkého vodíku“, z nichž každé má jeden proton a jeden neutron. K dosažení tohoto oddělení je třeba vynaložit velké množství vnější energie a zjistí se, že celková hmotnost dvou jader těžkého vodíku je měřitelně (asi o půl procenta) těžší než původní jádro helia. Tato extramasa, vynásobená c 2 , se právě rovná energii potřebné k rozdělení jádra hélia na dvě části. Ještě důležitější je, že tuto energii lze získat zpět tím, že se obě těžká vodíková jádra srazí a spojí a vytvoří opět jádro helia. (Obě jsou elektricky kladně nabita, takže se vzájemně odpuzují a musí se poměrně rychle sblížit, aby toto odpuzování překonala a dostala se do blízkosti, kde začne působit mnohem silnější jaderná přitažlivost.) To je základní zdroj energie vodíkové bomby a Slunce.

Ukazuje se, že všechny formy energie, kinetická i různé druhy potenciální energie, mají přidruženou hmotnost danou vztahem E=m c 2 . U jaderných reakcí je změna hmotnosti typicky v řádu tisícin celkové hmotnosti a je snadno měřitelná. U chemických reakcí je tato změna řádově miliardtina celkové hmotnosti a není v současné době měřitelná.

předchozí index

.