Gruppenmultiplikation
Nun werden wir untersuchen, was passiert, wenn wir zwei Symmetrieoperationen nacheinander anwenden. Betrachten wir als Beispiel das \(NH_3\)-Molekül, das zu der \(C_{3v}\)-Punktgruppe gehört. Was passiert, wenn wir eine \(C_3\)-Drehung gefolgt von einer \(\sigma_v\)-Reflexion anwenden? Wir schreiben diese kombinierte Operation \(\sigma_v\)\(C_3\) (Symmetrieoperationen wirken auf das, was direkt rechts von ihnen liegt, genau wie Operatoren in der Quantenmechanik – wir müssen also von rechts nach links rückwärts arbeiten, um die richtige Reihenfolge zu erhalten, in der die Operatoren angewendet werden). Wie wir bald sehen werden, ist die Reihenfolge, in der die Operationen angewendet werden, wichtig.
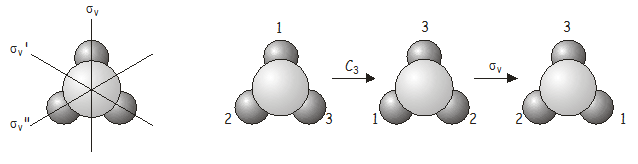
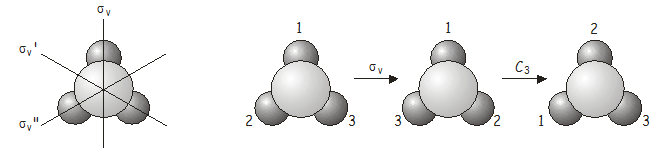
Auch die kombinierte Operation \(C_3\)\(\sigma_v\) ist äquivalent zu einer anderen Operation der Punktgruppe, diesmal \(\sigma_v’\).
Es gibt zwei wichtige Punkte, die durch dieses Beispiel veranschaulicht werden:
Die Auswirkungen der Anwendung von zwei Symmetrieoperationen nacheinander innerhalb einer gegebenen Punktgruppe werden in Gruppenmultiplikationstabellen zusammengefasst. Als Beispiel ist die vollständige Gruppenmultiplikationstabelle für \(C_{3v}\) unter Verwendung der Symmetrieoperationen, wie sie in den obigen Abbildungen definiert sind, unten dargestellt. Die Operationen in der ersten Zeile der Tabelle werden zuerst ausgeführt, gefolgt von den Operationen in der ersten Spalte (beachten Sie, dass sich die Tabelle ändern würde, wenn wir \(\sigma_v\), \(\sigma_v’\) und \(\sigma_v“\) in einer anderen Reihenfolge benennen würden).