Alai

In der mathematischen Analysis ordnet die uniform norm (oder sup norm) reellen oder komplexwertigen beschränkten Funktionen f, die auf einer Menge S definiert sind, die nichtnegative Zahl

Der Umfang des Quadrats ist die Menge der Punkte in R2, bei denen die sup norm gleich einer festen positiven Konstanten ist.

‖ f ‖ ∞ = ‖ f ‖ ∞ , S = sup { | f ( x ) | : x ∈ S } . {\displaystyle \|f\|_{\infty }=\|f\|_{\infty ,S}=\sup \left\{\,\left|f(x)\right|:x\in S\,\right\}.}

Diese Norm wird auch Supremumsnorm, Tschebyscheff-Norm, Unendlichkeitsnorm oder, wenn das Supremum tatsächlich das Maximum ist, Max-Norm genannt. Der Name „einheitliche Norm“ leitet sich von der Tatsache ab, dass eine Folge von Funktionen { f n } {\displaystyle \{f_{n}\}} zu f {\displaystyle f} unter der von der einheitlichen Norm abgeleiteten Metrik, wenn und nur wenn f n {\displaystyle f_{n}} zu f {\displaystyle f} gleichmäßig konvergiert.

Die durch diese Norm erzeugte Metrik wird Tschebyscheff-Metrik genannt, nach Pafnuty Tschebyscheff, der sie als erster systematisch untersucht hat.

Wenn wir unbeschränkte Funktionen zulassen, liefert diese Formel keine Norm oder Metrik im strengen Sinne, obwohl die erhaltene so genannte erweiterte Metrik immer noch erlaubt, eine Topologie auf dem fraglichen Funktionsraum zu definieren.

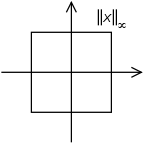
Ist f eine stetige Funktion auf einem geschlossenen Intervall oder allgemeiner einer kompakten Menge, dann ist sie beschränkt und das Supremum in der obigen Definition wird durch den Extremwertsatz von Weierstraß erreicht, so dass wir das Supremum durch das Maximum ersetzen können. Insbesondere für den Fall eines Vektors x = ( x 1 , … , x n ) {\displaystyle x=(x_{1},\dots ,x_{n})} ist die Norm auch die Maximalnorm. im endlichdimensionalen Koordinatenraum, hat sie die Form

‖ x ‖ ∞ = max { | x 1 | , … , | x n | } . {‖ ‖ ∞ = max { | x 1 | , … , | x n | }.

Der Grund für den Index „∞“ ist, dass, wenn f stetig ist

lim p → ∞ ‖ f ‖ p = ‖ f ‖ ∞ , {\displaystyle \lim _{p\rightarrow \infty }\|f\|_{p}=\|f\|_{\infty },}

wobei

‖ f ‖ p = ( ∫ D | f | p d μ ) 1 / p {\displaystyle \|f\|_{p}=\left(\int _{D}\left|f\right|^{p}\,d\mu \right)^{1/p}}

wobei D das Gebiet von f ist (und das Integral auf eine Summe hinausläuft, wenn D eine diskrete Menge ist).

Die Binärfunktion

d ( f , g ) = ‖ f – g ‖ ∞ {\displaystyle d(f,g)=\|f-g\|_{\infty }}

ist dann eine Metrik auf dem Raum aller beschränkten Funktionen (und offensichtlich jeder ihrer Teilmengen) auf einem bestimmten Gebiet. Eine Folge { fn : n = 1, 2, 3, … } konvergiert gleichförmig zu einer Funktion f, wenn und nur wenn

lim n → ∞ ‖ f n – f ‖ ∞ = 0. {displaystyle \lim _{n\rightarrow \infty }\|f_{n}-f\|_{\infty }=0.\,}

Wir können geschlossene Mengen und Abschlüsse von Mengen in Bezug auf diese metrische Topologie definieren; geschlossene Mengen in der einheitlichen Norm werden manchmal einheitlich geschlossen und Abschlüsse einheitliche Abschlüsse genannt. Die einheitliche Schließung einer Menge von Funktionen A ist der Raum aller Funktionen, die durch eine Folge von gleichförmig konvergierenden Funktionen auf A approximiert werden können. Eine Umformulierung des Satzes von Stone-Weierstraß lautet zum Beispiel, dass die Menge aller stetigen Funktionen auf {\displaystyle } der einheitliche Abschluss der Menge der Polynome auf {\displaystyle } .

Für komplexe stetige Funktionen über einem kompakten Raum wird dieser dadurch zu einer C*-Algebra.