Die folgende Definition der robusten Statistik stammt aus P. J. Hubers Buch Robust Statistics.
… jedes statistische Verfahren sollte die folgenden wünschenswerten Eigenschaften besitzen:
- Es sollte eine einigermaßen gute (optimale oder nahezu optimale) Effizienz bei dem angenommenen Modell haben.
- Es sollte robust in dem Sinne sein, dass kleine Abweichungen von den Modellannahmen die Leistung nur geringfügig beeinträchtigen sollten. …
- Etwas größere Abweichungen vom Modell sollten nicht zu einer Katastrophe führen.
Die klassische Statistik konzentriert sich auf den ersten von Hubers Punkten, indem sie Methoden entwickelt, die unter bestimmten Kriterien optimal sind. Dieser Beitrag befasst sich mit den kanonischen Beispielen, die zur Veranschaulichung von Hubers zweitem und drittem Punkt verwendet werden.
Hubers dritter Punkt wird normalerweise durch den Stichprobenmittelwert (Durchschnitt) und den Stichprobenmedian (Mittelwert) veranschaulicht. Man kann fast die Hälfte der Daten in einer Stichprobe auf ∞ setzen, ohne dass der Stichprobenmedian unendlich wird. Der Stichprobenmittelwert hingegen wird unendlich, wenn irgendein Stichprobenwert unendlich ist. Große Abweichungen vom Modell, d.h. ein paar Ausreißer, könnten eine Katastrophe für den Stichprobenmittelwert, aber nicht für den Stichprobenmedian verursachen.
Das kanonische Beispiel für die Diskussion von Hubers zweitem Punkt geht auf John Tukey zurück. Beginnen wir mit dem einfachsten Lehrbuchbeispiel der Schätzung: Daten aus einer Normalverteilung mit unbekanntem Mittelwert und Varianz 1, d.h. die Daten sind normal(μ, 1) mit unbekanntem μ. Die effizienteste Art, μ zu schätzen, ist die Verwendung des Stichprobenmittelwerts, des Durchschnitts der Daten.
Angenommen, die Datenverteilung ist nicht genau normal(μ, 1), sondern eine Mischung aus einer Standardnormalverteilung und einer Normalverteilung mit einer anderen Varianz. Nehmen wir an, δ sei eine kleine Zahl, z. B. 0,01, und die Daten entstammen einer Normal(μ, 1)-Verteilung mit der Wahrscheinlichkeit 1-δ und einer Normal(μ, σ2)-Verteilung mit der Wahrscheinlichkeit δ. Diese Verteilung wird als „kontaminierte Normalverteilung“ bezeichnet, und die Zahl δ ist der Grad der Kontamination. Der Grund für die Verwendung des Modells der kontaminierten Normalverteilung ist, dass es sich um eine nicht normale Verteilung handelt, die für das Auge normal aussieht.
Wir könnten den Populationsmittelwert μ entweder anhand des Stichprobenmittelwerts oder des Stichprobenmedians schätzen. Wenn die Daten streng normal und nicht gemischt sind, wäre der Stichprobenmittelwert der effizienteste Schätzer für μ. In diesem Fall wäre der Standardfehler etwa 25 % größer, wenn wir den Stichprobenmedian verwenden. Wenn die Daten jedoch aus einem Gemisch stammen, kann der Stichprobenmedian effizienter sein, je nach den Größen von δ und σ. Hier ist eine Darstellung der ARE (asymptotische relative Effizienz) des Stichprobenmedians im Vergleich zum Stichprobenmittelwert als Funktion von σ, wenn δ = 0.01.
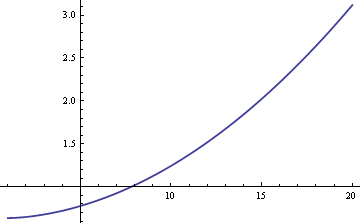
Die Darstellung zeigt, dass für Werte von σ größer als 8 der Stichprobenmedian effizienter ist als der Stichprobenmittelwert. Die relative Überlegenheit des Medians wächst unbegrenzt, wenn σ zunimmt.
Hier ist eine Darstellung der ARE mit σ fixiert auf 10 und δ variierend zwischen 0 und 1.
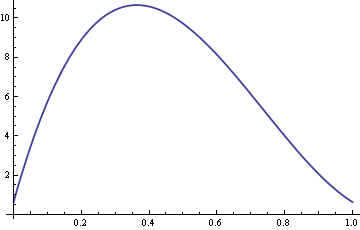
So für Werte von δ um 0.4 ist der Stichprobenmedian mehr als zehnmal effizienter als der Stichprobenmittelwert.
Die allgemeine Formel für den ARE in diesem Beispiel ist 2((1 + δ(σ2 – 1)(1 – δ + δ/σ)2)/ π.
Wenn Sie sicher sind, dass Ihre Daten normal und nicht oder nur sehr wenig kontaminiert sind, dann ist der Stichprobenmittelwert der effizienteste Schätzer. Es kann sich jedoch lohnen, das Risiko einzugehen, auf ein wenig Effizienz zu verzichten, wenn man weiß, dass man mit einem robusten Modell besser abschneidet, wenn eine erhebliche Kontamination vorliegt. Das Verlustpotenzial bei Verwendung des Stichprobenmittelwerts ist bei signifikanter Kontamination größer als der potenzielle Gewinn bei Verwendung des Stichprobenmittelwerts, wenn keine Kontamination vorliegt.
Hier ist ein Rätsel, das mit dem Beispiel der kontaminierten Normalen verbunden ist. Der effizienteste Schätzer für normal(μ, 1)-Daten ist der Stichprobenmittelwert. Und der effizienteste Schätzer für normal(μ, σ2)-Daten ist ebenfalls der Stichprobenmittelwert. Warum ist es dann nicht optimal, den Stichprobenmittelwert der Mischung zu nehmen?
Der Schlüssel ist, dass wir nicht wissen, ob eine bestimmte Stichprobe aus der Normal(μ, 1)-Verteilung oder aus der Normal(μ, σ2)-Verteilung stammt. Wenn wir das wüssten, könnten wir die Stichproben trennen, den Mittelwert getrennt bilden und die Stichproben zu einem Gesamtmittelwert zusammenfassen: einen Mittelwert mit 1-δ multiplizieren, den anderen mit δ multiplizieren und addieren. Da wir aber nicht wissen, welche der Mischungskomponenten zu welchen Proben führen, können wir die Proben nicht angemessen gewichten. (Wahrscheinlich kennen wir auch δ nicht, aber das ist ein anderes Thema.)
Es gibt andere Möglichkeiten als die Verwendung von Stichprobenmittelwert oder Stichprobenmedian. Beim getrimmten Mittelwert werden zum Beispiel einige der größten und kleinsten Werte herausgenommen und der Rest gemittelt. (Manchmal wird im Sport so verfahren, indem die höchste und die niedrigste Bewertung eines Sportlers von den Kampfrichtern gestrichen wird). Je mehr Daten auf beiden Seiten wegfallen, desto mehr verhält sich der getrimmte Mittelwert wie der Median der Stichprobe. Je weniger Daten weggeworfen werden, desto mehr verhält er sich wie der Stichprobenmittelwert.
Verwandter Beitrag: Effizienz von Median und Mittelwert bei Student-t-Verteilungen
Für tägliche Tipps zur Datenwissenschaft, folgen Sie @DataSciFact auf Twitter.