Alai

Michael Fowler,UVa Physics.

Der Impuls hat eine Richtung

Wie wir in der letzten Vorlesung besprochen haben, hatte Descartes, noch bevor Newton seine Gesetze formulierte, mit ein wenig Hilfe von Huygens, eine tiefgreifende dynamische Wahrheit entdeckt: bei jeder Kollision oder tatsächlich bei jeder Wechselwirkung jeglicher Art blieb der Gesamtbetrag des „Impulses“ – ein Maß für die Bewegung – immer gleich. Der Impuls eines sich bewegenden Objekts ist definiert als das Produkt aus Masse und Geschwindigkeit und ist somit ein Vektor: Er hat einen Betrag und eine Richtung. Wenn du auf reibungsfreien Schlittschuhen stehst und einen Ball wirfst, bewegst du dich rückwärts: Dein Impuls ist gleich groß, aber entgegengesetzt gerichtet wie der des Balls, so dass der Gesamtimpuls (dein Impuls und der des Balls) gleich Null bleibt. Raketen funktionieren auf die gleiche Weise, indem sie Material mit hoher Geschwindigkeit ausstoßen. Sie funktionieren nicht, indem sie „gegen die Luft stoßen“, sondern indem sie gegen das Material stoßen, das sie ausstoßen, so wie du gegen einen Ball stößt, den du wirfst, und er dich zurückstößt, was deine Beschleunigung verursacht.

Wenn du immer noch glaubst, dass Raketen wirklich gegen die Luft drücken, bedenke, dass sie im Weltraum genauso gut funktionieren! Als Goddard, ein früher amerikanischer Raketenforscher (das Goddard Space Flight Center ist nach ihm benannt), über Raketen im Weltraum sprach, glaubte man allgemein, dass er seine Zeit verschwendete. Ich zitiere aus einem Leitartikel der New York Times aus dem Jahr 1921: „Professor Goddard kennt nicht die Beziehung zwischen Aktion und Reaktion und die Notwendigkeit, etwas Besseres als ein Vakuum zu haben, gegen das man reagieren kann. Ihm scheint das Grundwissen zu fehlen, das täglich in unseren High Schools vermittelt wird.“ Offensichtlich haben die damaligen Redakteure der New York Times das Grundwissen, das in diesem Kurs vermittelt wird, nicht verstanden!

In der Tat, wie wir besprochen haben, folgt die Impulserhaltung bei einer Kollision aus den Newtonschen Gesetzen. Es handelt sich jedoch um ein allgemeineres, einfacheres Konzept – es hängt überhaupt nicht von den Einzelheiten der Wechselwirkungen usw. ab. Diese Einfachheit gefiel Einstein offensichtlich, denn er war überzeugt, dass die Impulserhaltung in jedem Inertialsystem auch dann noch gelten sollte, wenn die Dynamik unter Berücksichtigung der neuen Vorstellungen von Zeit und Raum neu formuliert würde. Dies führte ihn zu einigen überraschenden Schlussfolgerungen, wie wir sehen werden.

Drehmomenterhaltung auf dem Billardtisch

Zum Aufwärmen betrachten wir die Impulserhaltung beim Zusammenstoß zweier Kugeln auf einem Billardtisch. Wir ziehen eine Kreidelinie in der Mitte des Billardtisches und schießen die Kugeln von beiden Enden aus mit gleicher Geschwindigkeit in die Nähe der Kreidelinie, aber auf entgegengesetzte Seiten, so dass sie in der Mitte mit einem Schlag zusammenstoßen, der ihre Geschwindigkeiten um einen kleinen Winkel dreht. Mit anderen Worten, wenn wir sagen, dass ihre (gleich großen, entgegengesetzten) Geschwindigkeiten anfangs parallel zur x-Richtung – der Kreidelinie – waren, dann werden sie nach dem Zusammenstoß auch gleiche und entgegengesetzte kleine Geschwindigkeiten in y-Richtung haben (die Geschwindigkeiten in x-Richtung werden sehr leicht abgenommen haben).

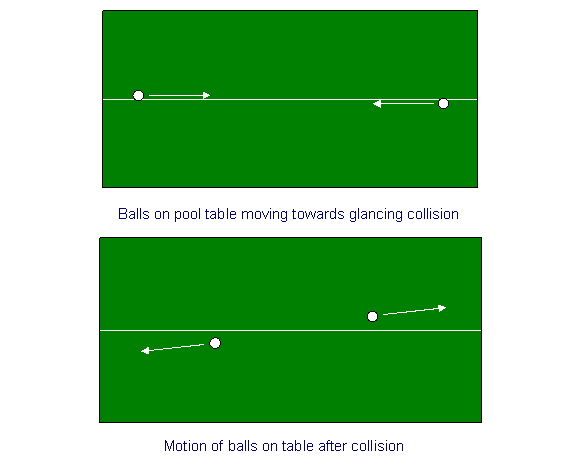
Eine symmetrische Raumschiffkollision

Nun wollen wir die Übung im großen Maßstab wiederholen. Nehmen wir an, dass wir irgendwo im Weltraum, weit weg von allen Gravitationsfeldern, einen Faden von einer Million Meilen Länge auslegen. (Sie könnte sich zwischen unseren beiden Uhren im Zeitdilatationsexperiment befinden). Diese Schnur entspricht der Kreidelinie auf dem Billardtisch. Nehmen wir nun an, dass sich zwei identische Raumschiffe mit gleicher und entgegengesetzter Geschwindigkeit parallel zur Schnur von den beiden Enden der Schnur aus nähern und so ausgerichtet sind, dass sie einen leichten Zusammenstoß erleiden, wenn sie sich in der Mitte treffen. Aus der Symmetrie der Situation ergibt sich, dass der Impuls in beiden Richtungen erhalten bleibt. Insbesondere ist die Geschwindigkeit, mit der sich das eine Raumschiff nach der Kollision von der Schnur wegbewegt – seine y-Geschwindigkeit – gleich und entgegengesetzt zu der Geschwindigkeit, mit der sich das andere von der Schnur wegbewegt.

Betrachten wir nun diesen Zusammenstoß, wie er von jemandem in einem der Raumschiffe beobachtet wird, nennen wir ihn A. Vor dem Zusammenstoß sieht er die Schnur, die sich sehr schnell am Fenster bewegt, sagen wir ein paar Meter entfernt. Nach der Kollision sieht er, dass sich die Schnur mit, sagen wir, 15 Metern pro Sekunde wegbewegt. Das liegt daran, dass das Raumschiff Ah eine Geschwindigkeit von 15 Metern pro Sekunde senkrecht zur Schnur angenommen hat. Da es sich um eine vollkommen symmetrische Situation handelt, würde ein Beobachter auf Raumschiff B mit Sicherheit folgern, dass sich sein Raumschiff ebenfalls mit 15 Metern pro Sekunde von der Schnur wegbewegt.

Wie symmetrisch ist es denn?

Die entscheidende Frage ist: Wie schnell bewegt sich Raumschiff B aus der Sicht eines Beobachters von Raumschiff A von der Schnur weg? Nehmen wir an, dass sich Raumschiff B relativ zu Raumschiff A mit 0,6c (in x-Richtung) entfernt. Zunächst sei daran erinnert, dass Abstände senkrecht zur Bewegungsrichtung nicht Lorentz-kontrahiert sind. Wenn also der Beobachter in Raumschiff B sagt, dass sie sich in einem Zeitintervall von einer Sekunde 15 Meter weiter von der Schnur entfernt hat, wird der Beobachter, der diese Bewegung von Raumschiff A aus beobachtet, den 15 Metern zustimmen – aber der einen Sekunde nicht zustimmen! Er wird sagen, dass ihre Uhren langsam gehen, so dass nach seinen Uhren 1,25 Sekunden verstrichen sind, als sie sich 15 Meter in y-Richtung bewegt.

Daraus folgt, dass diese Kollision aus Sicht von Raumschiff A aufgrund der Zeitdilatation nicht zu gleichen und entgegengesetzten Geschwindigkeiten der beiden Raumschiffe in y-Richtung führt. Ursprünglich bewegten sich beide Raumschiffe parallel zur x-Achse, es gab ein Nullmoment in y-Richtung. Wie kann man also argumentieren, dass es nach der Kollision keinen Gesamtimpuls in y-Richtung gibt, wenn die identischen Raumschiffe nicht die gleichen und entgegengesetzten Geschwindigkeiten haben?

Einstein rettet die Impulserhaltung

Einstein war sich so sicher, dass die Impulserhaltung immer gelten muss, dass er sie mit einer gewagten Hypothese rettete: Die Masse eines Objekts muss von seiner Geschwindigkeit abhängen! In der Tat muss die Masse mit der Geschwindigkeit so zunehmen, dass die aus der Zeitdilatation resultierende geringere Geschwindigkeit in y-Richtung aufgehoben wird. Das heißt, wenn ein ruhendes Objekt die Masse m hat und sich mit der Geschwindigkeit v bewegt, hat es eine Trägheit, die einer „relativistischen Masse“ m rel =m/ 1-( v 2 / c 2 ) entspricht, dann wird der Impuls zu

p → = m rel v → =m v → / 1-( v 2 / c 2 ) .

Man beachte, dass diese relativistische Massenzunahme bei gewöhnlichen Geschwindigkeiten ein unmerklich kleiner Effekt ist, aber wenn sich ein Objekt der Fluggeschwindigkeit nähert, nimmt die Masse unbegrenzt zu!

Die Masse nimmt wirklich mit der Geschwindigkeit zu

Die Entscheidung, dass die Masse von Objekten von der Geschwindigkeit abhängen muss, scheint ein hoher Preis zu sein, um die Erhaltung des Impulses zu retten! Es handelt sich jedoch um eine Vorhersage, die sich leicht durch Experimente überprüfen lässt. Die erste Bestätigung erfolgte 1908 durch die Ablenkung von schnellen Elektronen in einer Vakuumröhre. Tatsächlich haben die Elektronen in einer alten Farbfernsehröhre etwa ein halbes Prozent mehr Trägheit als ruhende Elektronen, was bei der Berechnung der Magnetfelder berücksichtigt werden muss, mit denen sie auf den Bildschirm gelenkt werden.

Viel dramatischer ist, dass in modernen Teilchenbeschleunigern sehr starke elektrische Felder verwendet werden, um Elektronen, Protonen und andere Teilchen zu beschleunigen. In der Praxis zeigt sich, dass diese Teilchen immer größere Kräfte zur weiteren Beschleunigung benötigen, je mehr man sich der Lichtgeschwindigkeit nähert. Folglich ist die Lichtgeschwindigkeit eine natürliche absolute Geschwindigkeitsgrenze. Teilchen werden auf Geschwindigkeiten beschleunigt, bei denen ihre relativistische Masse tausendmal größer ist als ihre in Ruhe gemessene Masse, die gewöhnlich als „Ruhemasse“ bezeichnet wird.

…oder doch nicht?

In der Tat gibt es unter Physikern eine anhaltende Debatte über das Konzept der relativistischen Masse. Die Debatte ist weitgehend semantisch: Niemand bezweifelt, dass der korrekte Ausdruck für den Impuls eines Teilchens mit der Ruhemasse m, das sich mit der Geschwindigkeit v → bewegt, p → = m 1- v 2 / c 2 v → ist. Aber vor allem Teilchenphysiker, von denen viele ihr Leben damit verbringen, die Ruhemasse von Teilchen mit großer Präzision zu messen, sind nicht scharf darauf, dies als p → = m rel v → zu schreiben. Sie mögen die Idee einer variablen Masse nicht. Zum einen könnte dies den Eindruck erwecken, dass sich ein Teilchen mit zunehmender Geschwindigkeit aufbläht oder sich zumindest seine innere Struktur irgendwie verändert. Tatsächlich erfährt ein relativistisches Teilchen lediglich eine Lorentz-Kontraktion entlang der Bewegungsrichtung, wie alles andere auch. Es geht von einer Kugelform zu einer scheibenförmigen Form mit gleichem Querradius über.

Wie ist nun diese „Massenzunahme“ zu verstehen? Wie immer hatte Einstein recht: Er bemerkte, dass jede Form von Energie eine Trägheit besitzt. Die kinetische Energie selbst hat eine Trägheit. Nun ist „Trägheit“ eine definierende Eigenschaft der Masse. Die andere fundamentale Eigenschaft der Masse ist, dass sie durch die Schwerkraft angezogen wird. Tut diese kinetische Energie das auch? Um die Antwort zu sehen, betrachten Sie eine mit Gas gefüllte Kugel. Sie wird ein sphärisch symmetrisches Gravitationsfeld außerhalb ihrer selbst erzeugen, dessen Stärke proportional zur Gesamtmasse ist. Wenn wir nun das Gas aufheizen, haben die Gasteilchen diese erhöhte (relativistische) Masse, die ihrer erhöhten kinetischen Energie entspricht, und das äußere Gravitationsfeld hat sich proportional dazu erhöht. (Beides wird von niemandem bezweifelt.)

Die „relativistische Masse“ hat also in der Tat die beiden grundlegenden Eigenschaften der Masse: Trägheit und Gravitationsanziehung. (Wie in den folgenden Vorlesungen deutlich wird, ist diese relativistische Masse nichts anderes als die Gesamtenergie, wobei die Ruhemasse selbst nun als Energie betrachtet wird.)

Auf einer trivialeren Ebene haben einige Lehrer Einwände gegen die Einführung der relativistischen Masse, weil sie befürchten, dass die Schüler annehmen, die kinetische Energie eines relativistisch bewegten Teilchens sei einfach 1 2 m v → 2, wenn man die relativistische Masse verwendet – das ist sie nicht, wie wir gleich sehen werden.

Fußnote: Für alle, die vielleicht irgendwann einmal zu einer mathematisch anspruchsvolleren Behandlung übergehen, sei hinzugefügt, dass die Ruhemasse als Invariante beim Übergang von einem Bezugssystem zum anderen eine wichtige Rolle spielt, aber die hier verwendete „relativistische Masse“ ist eigentlich nur die erste Komponente (die Energie) des vierdimensionalen Energie-Impuls-Vektors eines Teilchens und damit keine Invariante.

Kinetische Energie und Masse für sehr schnelle Teilchen

Betrachten wir nun die kinetische Energie eines dieser Teilchen, das sich nahe der Lichtgeschwindigkeit bewegt. Erinnern Sie sich, dass wir in einer früheren Vorlesung herausgefunden haben, dass die kinetische Energie einer gewöhnlichen nichtrelativistischen (d.h. sich langsam bewegenden) Masse m 1 2 m v 2 beträgt. Dazu haben wir uns überlegt, wie viel Arbeit wir leisten mussten, um die Masse über eine bestimmte Höhe zu heben: Wir mussten eine Kraft ausüben, die ihrem Gewicht W entsprach, um sie über die Höhe h zu heben, wobei die gesamte geleistete Arbeit bzw. die aufgewendete Energie Kraft x Entfernung, Wh, war. Als es wieder nach unten fiel, verrichtete die Schwerkraft W genau die gleiche Arbeit Wh am fallenden Objekt, aber dieses Mal wurde die Arbeit zur Beschleunigung des Objekts verwendet, um ihm kinetische Energie zu verleihen. Da wir wissen, wie schnell fallende Objekte ihre Geschwindigkeit aufnehmen, konnten wir schließen, dass die kinetische Energie 1 2 m v 2 beträgt. (Näheres dazu in der vorhergehenden Vorlesung.)

Allgemeiner ausgedrückt: Wir hätten die Masse mit einer beliebigen konstanten Kraft F beschleunigen können und die von der Kraft verrichtete Arbeit (Kraft x Strecke) ermitteln können, um sie aus dem Stand auf die Geschwindigkeit v zu bringen. Die kinetische Energie der Masse, E= 1 2 m v 2 , ist genau gleich der Arbeit, die die Kraft geleistet hat, um die Masse auf diese Geschwindigkeit zu bringen. (In ähnlicher Weise kann man zeigen, dass, wenn man auf ein Teilchen, das sich bereits mit der Geschwindigkeit u bewegt, eine Kraft ausübt und es auf die Geschwindigkeit v beschleunigt, die notwendige Arbeit 1 2 m v 2 – 1 2 m u 2 beträgt.)

Es ist interessant, die Übung für ein Teilchen zu wiederholen, das sich sehr nahe an der Lichtgeschwindigkeit bewegt, wie die Teilchen in den im vorigen Absatz erwähnten Beschleunigern. Das Zweite Newtonsche Gesetz in der Form

Kraft = Impulsänderungsrate

ist immer noch wahr, aber in der Nähe der Lichtgeschwindigkeit ändert sich die Geschwindigkeit nur unwesentlich, während die Kraft weiter wirkt – stattdessen nimmt die Masse zu! Daher können wir in guter Näherung schreiben:

Kraft = (Änderungsrate der Masse) x c

wobei wie üblich c die Lichtgeschwindigkeit ist. Um genauer zu werden, nehmen wir an, dass eine konstante Kraft F ein Teilchen antreibt. Zu einem bestimmten Zeitpunkt hat das Teilchen die Masse M und eine Geschwindigkeit, die extrem nahe bei c liegt. Eine Sekunde später, da die Kraft weiterhin auf das Teilchen einwirkt und somit seinen Impuls nach dem Zweiten Newtonschen Gesetz erhöht, hat das Teilchen die Masse M+m, wobei m die Massenzunahme infolge der Einwirkung der Kraft ist.

Wie hoch ist die Zunahme der kinetischen Energie E des Teilchens während dieser einen Sekunde? In exakter Analogie zu dem oben betrachteten nichtrelativistischen Fall ist es einfach die Arbeit, die die Kraft in diesem Zeitraum verrichtet. Da sich nun die Masse des Teilchens in einer Sekunde um m ändert, ist m auch die Änderungsrate der Masse. Daher können wir aus Newtons zweitem Gesetz in der Form

Kraft = (Änderungsrate der Masse) x c,

schreiben

Kraft =mc.

Die Zunahme der kinetischen Energie E über den Zeitraum von einer Sekunde ist nur die von der Kraft geleistete Arbeit,

E= Kraft x Strecke.

Da sich das Teilchen im Wesentlichen mit Lichtgeschwindigkeit bewegt, beträgt die Strecke, über die die Kraft in der Sekunde wirkt, nur c Meter, c=3× 10 8 .

Die Gesamtarbeit, die die Kraft in dieser Sekunde leistet, ist also Kraft x Strecke =mc×c=m c 2 .

Das Verhältnis zwischen der Massenzunahme des relativistischen Teilchens und seiner Zunahme der kinetischen Energie ist also:

E=m c 2 .

Kinetische Energie und Masse für langsame Teilchen

Erinnern wir uns daran, dass wir, damit die Newtonschen Gesetze in allen Inertialsystemen gelten, eine Zunahme der Masse mit der Geschwindigkeit um den Faktor 1/ 1-( v 2 / c 2 ) annehmen mussten. Das bedeutet, dass selbst ein sich langsam bewegendes Objekt eine winzige Massenzunahme hat, wenn es sich bewegt!

Wie hängt diese winzige Zunahme mit der kinetischen Energie zusammen? Betrachten wir eine Masse M, die sich mit einer Geschwindigkeit v bewegt, die viel kleiner als die Lichtgeschwindigkeit ist. Ihre kinetische Energie E= 1 2 M v 2 , wie oben beschrieben. Ihre Masse ist M/ 1-( v 2 / c 2 ), was wir als M+m schreiben können. Wie groß ist m?

Da wir von Geschwindigkeiten sprechen, die uns vertraut sind, wie z.B. bei einem Düsenflugzeug, wo v/c sehr klein ist, können wir einige einfache mathematische Tricks anwenden, um die Sache zu erleichtern.

Der erste ist eine gute Näherung für die Quadratwurzel aus 1-x, wenn x viel kleiner als eins ist:

1-x ≅1- 1 2 x für x≪1.

Das kannst du leicht mit deinem Taschenrechner überprüfen: versuche x= 1 100 , du findest 99 100 =0.994987… was extrem nah an 1- 1 2 1 100 =0.995 ist !

Die nächste Annäherung ist

1 1-x ≅1+x für x≪1.

Auch das lässt sich leicht überprüfen: man nehme wieder x= 1 100 : 1 1-x = 1 99 100 = 100 99 =1,01010… ,und 1+x= 101 100 =1,01.

Wenn wir diese Näherungen mit x=v/c verwenden, können wir 1-( v 2 / c 2 ) als 1- 1 2 ( v 2 / c 2 ) , und dann 1/( 1- 1 2 ( v 2 / c 2 ) ) als 1+ 1 2 ( v 2 / c 2 ) annähern.

Das bedeutet, dass die Gesamtmasse bei der Geschwindigkeit v

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ),

und wenn wir dies als M+m schreiben, sehen wir, dass die Massenzunahme m gleich 1 2 M v 2 / c 2 ist.

Das bedeutet, dass – wiederum – die Massenzunahme m mit der kinetischen Energie E durch E=m c 2 zusammenhängt.

In der Tat ist es nicht schwer, mit ein wenig Rechenarbeit zu zeigen, dass ein bewegtes Teilchen über den gesamten Geschwindigkeitsbereich von Null bis nahe an die Lichtgeschwindigkeit eine Massenzunahme erfährt, die mit der kinetischen Energie E=m c 2 in Beziehung steht. Um zu verstehen, warum dies im Alltag nicht bemerkt wird, versuchen Sie es mit einem Beispiel, z. B. einem Flugzeug mit einem Gewicht von 100 Tonnen, das sich mit 2.000 km/h bewegt. 100 Tonnen sind 100.000 Kilogramm, 2.000 mph sind etwa 1.000 Meter pro Sekunde. Das ist eine kinetische Energie 1 2 M v 2 von ½ ×1011 Joule, aber die entsprechende Massenänderung des Flugzeugs um den Faktor c 2 , 9× 10 16 , was eine tatsächliche Massenzunahme von etwa einem halben Milligramm ergibt, nicht so einfach zu erkennen!

E = mc2

Wir haben oben gesehen, dass, wenn eine Kraft Arbeit verrichtet, die einen Körper beschleunigt, um ihm kinetische Energie zu verleihen, die Masse des Körpers um einen Betrag zunimmt, der gleich der gesamten von der Kraft verrichteten Arbeit, der übertragenen Energie E, dividiert durch c 2 , ist. Wie verhält es sich, wenn eine Kraft Arbeit auf einen Körper ausübt, die ihn nicht beschleunigt, so dass es keine Zunahme der kinetischen Energie gibt? Was ist zum Beispiel, wenn ich etwas mit gleichbleibender Geschwindigkeit anhebe und ihm damit potenzielle Energie gebe? Es stellt sich heraus, dass es auch in diesem Fall eine Massenzunahme gibt, die durch E=m c 2 gegeben ist, natürlich unmessbar klein für Alltagsgegenstände.

In der Kernphysik ist dies jedoch ein messbarer und wichtiger Effekt. Zum Beispiel hat das Heliumatom einen Kern, der aus zwei Protonen und zwei Neutronen besteht, die durch eine starke Kernanziehungskraft sehr eng aneinander gebunden sind. Bei ausreichender äußerer Krafteinwirkung kann dieser Kern in zwei „schwere Wasserstoffkerne“ mit je einem Proton und einem Neutron gespalten werden. Um diese Trennung zu erreichen, muss viel äußere Energie aufgewendet werden, und man stellt fest, dass die Gesamtmasse der beiden schweren Wasserstoffkerne messbar (etwa ein halbes Prozent) schwerer ist als die des ursprünglichen Heliumkerns. Diese Extramasse, multipliziert mit c 2 , entspricht genau der Energie, die für die Spaltung des Heliumkerns in zwei Teile benötigt wird. Noch wichtiger ist, dass diese Energie zurückgewonnen werden kann, indem man die beiden schweren Wasserstoffkerne zusammenstoßen und sich wieder zu einem Heliumkern vereinigen lässt. (Da beide elektrisch positiv geladen sind, stoßen sie sich gegenseitig ab und müssen sich ziemlich schnell annähern, um diese Abstoßung zu überwinden und die Nähe zu erreichen, bei der die viel stärkere Kernanziehung einsetzt.) Dies ist die grundlegende Energiequelle der Wasserstoffbombe und der Sonne.

Es stellt sich heraus, dass alle Formen von Energie, kinetische und verschiedene Arten von potenzieller Energie, eine Masse haben, die durch E=m c 2 gegeben ist. Bei Kernreaktionen liegt die Massenänderung in der Regel in der Größenordnung eines Tausendstels der Gesamtmasse und ist leicht messbar. Bei chemischen Reaktionen liegt die Änderung in der Größenordnung eines Milliardstels der Gesamtmasse und ist derzeit nicht messbar.

vorheriger Index