La siguiente definición de estadística robusta proviene del libro Robust Statistics de P. J. Huber.
… cualquier procedimiento estadístico debería poseer las siguientes características deseables:
- Debería tener una eficacia razonablemente buena (óptima o casi óptima) en el modelo asumido.
- Debería ser robusto en el sentido de que pequeñas desviaciones de los supuestos del modelo deberían perjudicar el rendimiento sólo ligeramente. …
- Las desviaciones algo mayores del modelo no deberían causar una catástrofe.
La estadística clásica se centra en el primero de los puntos de Huber, produciendo métodos que son óptimos sujetos a algunos criterios. Este artículo examina los ejemplos canónicos utilizados para ilustrar los puntos segundo y tercero de Huber.
El tercer punto de Huber se ilustra típicamente con la media muestral (promedio) y la mediana muestral (valor medio). Se puede ajustar casi la mitad de los datos de una muestra a ∞ sin que la mediana de la muestra se vuelva infinita. La media muestral, en cambio, se convierte en infinita si cualquier valor de la muestra es infinito. Las grandes desviaciones del modelo, es decir, unos pocos valores atípicos, podrían causar una catástrofe para la media de la muestra, pero no para la mediana de la muestra.
El ejemplo canónico al discutir el segundo punto de Huber se remonta a John Tukey. Comience con el ejemplo más simple de libro de texto de estimación: datos de una distribución normal con media desconocida y varianza 1, es decir, los datos son normales(μ, 1) con μ desconocido. La forma más eficiente de estimar μ es tomar la media muestral, el promedio de los datos.
Pero suponga ahora que la distribución de los datos no es exactamente normal(μ, 1) sino que es una mezcla de una distribución normal estándar y una distribución normal con una varianza diferente. Sea δ un número pequeño, digamos 0,01, y suponga que los datos proceden de una distribución normal(μ, 1) con probabilidad 1-δ y que los datos proceden de una distribución normal(μ, σ2) con probabilidad δ. Esta distribución se llama «normal contaminada» y el número δ es la cantidad de contaminación. La razón para utilizar el modelo normal contaminado es que se trata de una distribución no normal que puede parecer normal a simple vista.
Podríamos estimar la media poblacional μ utilizando la media muestral o la mediana muestral. Si los datos fueran estrictamente normales y no una mezcla, la media muestral sería el estimador más eficiente de μ. En ese caso, el error estándar sería aproximadamente un 25% mayor si utilizáramos la mediana muestral. Pero si los datos provienen de una mezcla, la mediana de la muestra puede ser más eficiente, dependiendo de los tamaños de δ y σ. Aquí hay un gráfico de la ARE (eficiencia relativa asintótica) de la mediana de la muestra en comparación con la media de la muestra en función de σ cuando δ = 0.01.
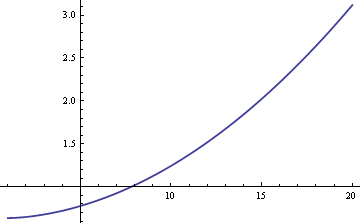
El gráfico muestra que para valores de σ superiores a 8, la mediana muestral es más eficiente que la media muestral. La superioridad relativa de la mediana crece sin límites a medida que aumenta σ.
Aquí se muestra un gráfico de la ARE con σ fijada en 10 y δ que varía entre 0 y 1.
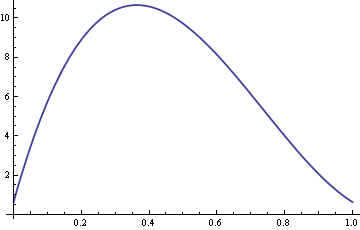
Así, para valores de δ en torno a 0.4, la mediana muestral es más de diez veces más eficiente que la media muestral.
La fórmula general para el ARE en este ejemplo es 2((1 + δ(σ2 – 1)(1 – δ + δ/σ)2)/ π.
Si está seguro de que sus datos son normales sin contaminación o con muy poca contaminación, entonces la media muestral es el estimador más eficiente. Pero puede valer la pena arriesgarse a renunciar a un poco de eficiencia a cambio de saber que lo hará mejor con un modelo robusto si hay una contaminación significativa. Hay más potencial de pérdida utilizando la media muestral cuando hay una contaminación significativa que la ganancia potencial utilizando la media muestral cuando no hay contaminación.
Aquí hay un enigma asociado con el ejemplo de la normal contaminada. El estimador más eficiente para datos normales(μ, 1) es la media muestral. Y el estimador más eficiente para datos normales(μ, σ2) es también tomar la media muestral. Entonces, ¿por qué no es óptimo tomar la media muestral de la mezcla?
La clave es que no sabemos si una muestra concreta procede de la distribución normal(μ, 1) o de la normal(μ, σ2). Si lo supiéramos, podríamos segregar las muestras, promediarlas por separado y combinar las muestras en una media agregada: multiplicar una media por 1-δ, multiplicar la otra por δ y sumar. Pero como no sabemos qué componentes de la mezcla dan lugar a qué muestras, no podemos ponderar las muestras adecuadamente. (Probablemente tampoco conozcamos δ, pero eso es otra cuestión.)
Hay otras opciones además de utilizar la media o la mediana muestral. Por ejemplo, la media recortada elimina algunos de los valores más grandes y más pequeños y luego promedia todo lo demás. (A veces los deportes funcionan de esta manera, desechando las marcas más altas y más bajas de un atleta por parte de los jueces). Cuantos más datos se descarten en cada extremo, más se asemeja la media recortada a la mediana de la muestra. Cuantos menos datos se desechen, más se comportará como la media de la muestra.
Puesto relacionado: Eficiencia de la mediana frente a la media para las distribuciones de Student-t
Para obtener consejos diarios sobre ciencia de datos, sigue a @DataSciFact en Twitter.