Multiplication de groupes
Nous allons maintenant étudier ce qui se passe lorsque nous appliquons deux opérations de symétrie à la suite. À titre d’exemple, considérons la molécule \(NH_3\), qui appartient au groupe ponctuel \(C_{3v}\). Imaginez ce qui se passe si nous appliquons une rotation \(C_3\) suivie d’une réflexion \(\sigma_v\). Nous écrivons cette opération combinée \(\sigma_v\)\(C_3\) (lorsqu’elles sont écrites, les opérations de symétrie opèrent sur la chose directement à leur droite, tout comme les opérateurs en mécanique quantique – nous devons donc travailler à rebours de droite à gauche à partir de la notation pour obtenir l’ordre correct dans lequel les opérateurs sont appliqués). Comme nous le verrons bientôt, l’ordre dans lequel les opérations sont appliquées est important.
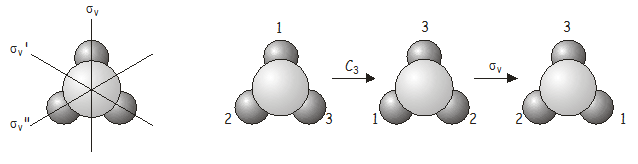
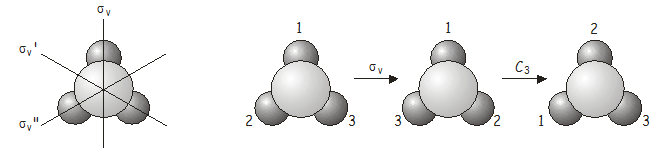
Encore, l’opération combinée \(C_3\)\(\sigma_v\) est équivalente à une autre opération du groupe de points, cette fois \(\sigma_v’\).
Deux points importants sont illustrés par cet exemple :
Les effets de l’application de deux opérations de symétrie en séquence dans un groupe ponctuel donné sont résumés dans les tables de multiplication de groupe. A titre d’exemple, la table de multiplication de groupe complète pour \(C_{3v}\) utilisant les opérations de symétrie telles que définies dans les figures ci-dessus est présentée ci-dessous. Les opérations écrites sur la première ligne de la table sont effectuées en premier, suivies de celles écrites dans la première colonne (notez que la table changerait si nous choisissions de nommer \(\sigma_v\), \(\sigma_v’\) et \(\sigma_v »\) dans un ordre différent).