
mise à jour : Nous avons introduit une App d’apprentissage interactive pour l’apprentissage automatique / IA ,>> Consultez-la gratuitement maintenant <<
Importer les bibliothèques requises
import numpy as np
import pandas as pd
eps = np.finfo(float).eps
from numpy import log2 as log
‘eps’ ici est le plus petit nombre représentable. Parfois, nous obtenons log(0) ou 0 dans le dénominateur, pour éviter cela, nous allons utiliser ceci.
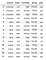
Définir le jeu de données :
Créer le dataframe pandas :
Maintenant essayons de nous souvenir des étapes pour créer un arbre de décision…..
1.compute the entropy for data-set2.for every attribute/feature:
1.calculate entropy for all categorical values
2.take average information entropy for the current attribute
3.calculate gain for the current attribute3. pick the highest gain attribute.
4. Repeat until we get the tree we desired
- trouver l’entropie puis le gain d’information pour diviser l’ensemble des données.
Nous allons définir une fonction qui prend en classe (vecteur variable cible) et trouve l’entropie de cette classe.
Ici la fraction est ‘pi’, c’est la proportion d’un nombre d’éléments dans ce groupe divisé par rapport au nombre d’éléments dans le groupe avant la division(groupe parent).

2 .Définissez maintenant une fonction {ent} pour calculer l’entropie de chaque attribut :
stockez l’entropie de chaque attribut avec son nom :
a_entropy = {k:ent(df,k) for k in df.keys()}
a_entropy

3. calculer le gain d’info de chaque attribut :
définir une fonction pour calculer l’IG (infogain) :
IG(attr) = entropie du jeu de données – entropie de l’attribut
def ig(e_dataset,e_attr):
return(e_dataset-e_attr)
stocker l’IG de chaque attr dans un dict :
#entropy_node = entropy of dataset
#a_entropy = entropy of k(th) attrIG = {k:ig(entropy_node,a_entropy) for k in a_entropy}

comme nous pouvons le voir outlook a le gain d’information le plus élevé de 0.24 , donc nous allons sélectionner outook comme le nœud à ce niveau pour le fractionnement.
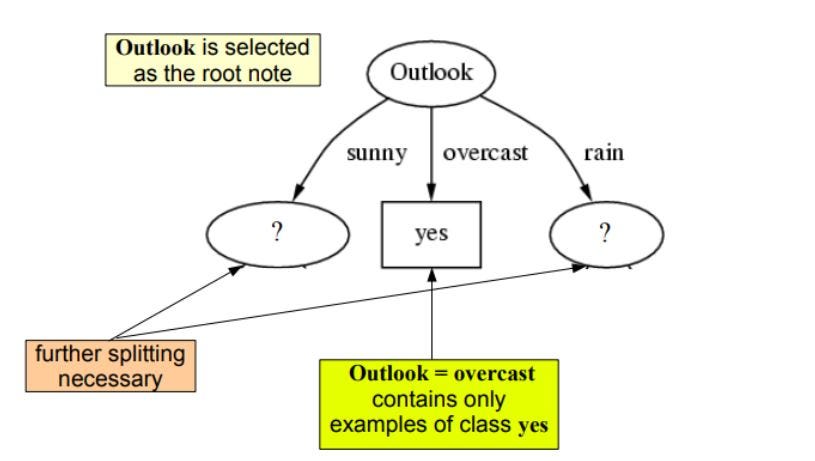
Maintenant pour procéder notre arbre nous allons utiliser la récursion
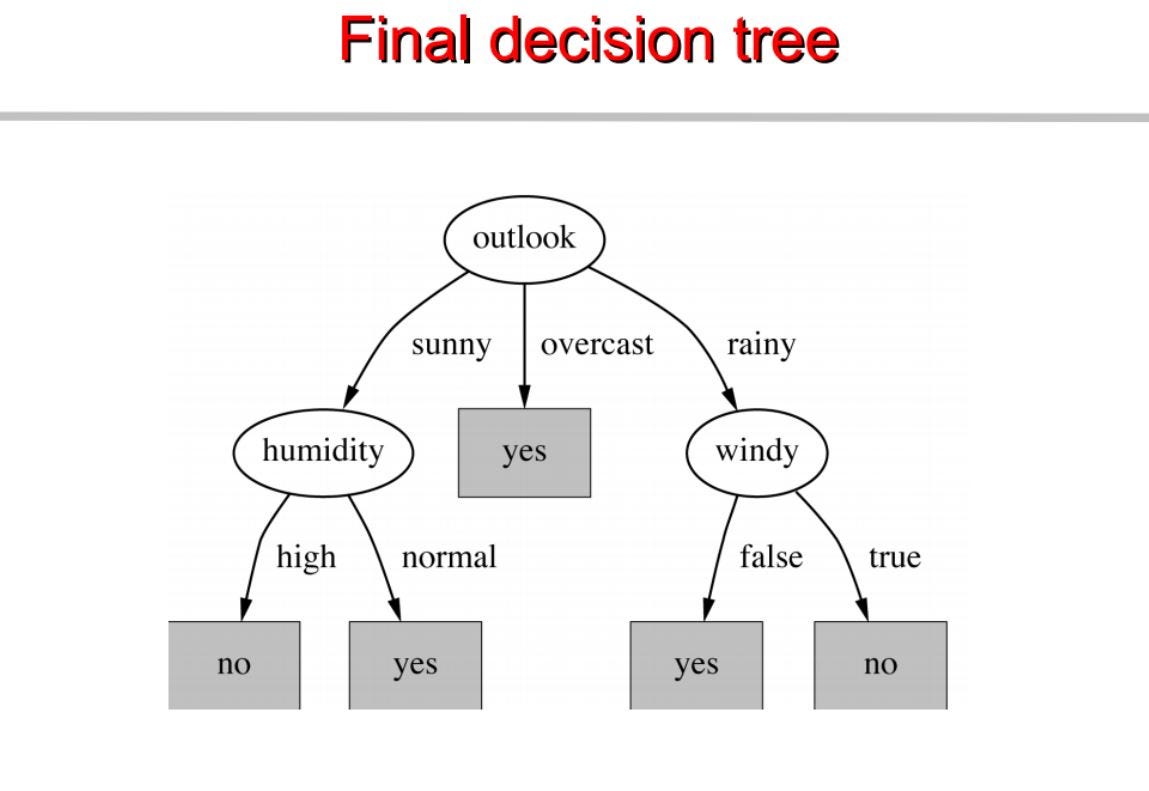
Répéter la même chose pour les sous-arbres jusqu’à obtenir l’arbre.

Nous construisons un arbre de décision basé sur cela. Voici le code complet.

visiter pytholabs.com pour des cours étonnants
.