Alai

Michael Fowler,UVa Physics.

Le momentum a une direction

Comme nous l’avons abordé dans le dernier cours, avant même que Newton ne formule ses lois, Descartes, avec un peu d’aide de Huygens, avait découvert une vérité dynamique profonde : dans toute collision, ou en fait dans toute interaction de quelque nature que ce soit, la quantité totale de « momentum » – une mesure du mouvement – est toujours restée la même. L’élan d’un objet en mouvement est défini comme le produit de la masse et de la vitesse, et c’est donc un vecteur : il a une magnitude et une direction. Si vous vous tenez debout sur des patins sans frottement et que vous lancez une balle, vous vous déplacez en arrière : vous avez une quantité de mouvement égale en magnitude, mais de direction opposée, à celle de la balle, de sorte que la quantité de mouvement totale (la vôtre plus celle de la balle) reste nulle. Les fusées fonctionnent de la même manière, en projetant de la matière à grande vitesse. Elles ne fonctionnent pas en « poussant contre l’air », elles fonctionnent en poussant contre la matière qu’elles expulsent, tout comme vous poussez contre une bally que vous lancez, et elle vous repousse, provoquant votre accélération.

Si vous soupçonnez encore que vraiment les fusées poussent contre l’air, rappelez-vous qu’elles fonctionnent tout aussi bien dans l’espace ! En fait, on croyait généralement que lorsque Goddard, un des premiers roquettistes américains (le Goddard Space Flight Center porte son nom) parlait de fusées dans l’espace, il perdait son temps. Pour citer un éditorial du New York Times écrit en 1921 : « Le professeur Goddard ne connaît pas la relation entre l’action et la réaction et la nécessité d’avoir quelque chose de mieux qu’un vide pour réagir. Il semble manquer des connaissances de base dispensées quotidiennement dans nos lycées ». De toute évidence, les éditorialistes du New York Times de l’époque ont manqué les connaissances de base dispensées à la louche dans ce cours !

En fait, comme nous l’avons discuté, la conservation de la quantité de mouvement dans une acollision découle des lois de Newton. Cependant, c’est un concept plus général, plus simple – il ne dépend pas du tout des détails des interactions, etc. Cette simplicité a manifestement séduit Einstein, qui était convaincu que lorsque la dynamique était reformulée pour inclure les nouvelles idées sur le temps et l’espace, la conservation de la quantité de mouvement devait rester vraie dans tout cadre inertiel. Cela l’a conduit à des conclusions surprenantes, comme nous allons le voir.

Conservation du momentum sur la table de billard

En guise d’exercice d’échauffement, considérons la conservation du momentum pour une collision de deux boules sur une table de billard. Nous traçons une ligne de craie au milieu de la table de billard, et nous tirons les boules près de la ligne de craie, mais sur des côtés opposés de celle-ci, à partir de chaque extrémité, à la même vitesse, de sorte qu’elles se heurteront au milieu avec un coup incident, ce qui fera tourner leurs vitesses d’un petit angle. En d’autres termes, si initialement nous disons que leurs vitesses (de même grandeur, de direction opposée)étaient parallèles à la direction x – la ligne de craie – alors après la collision, ils auront également de petites vitesses égales et opposées dans la direction y.(Les vitesses dans la direction x auront très légèrement diminué).

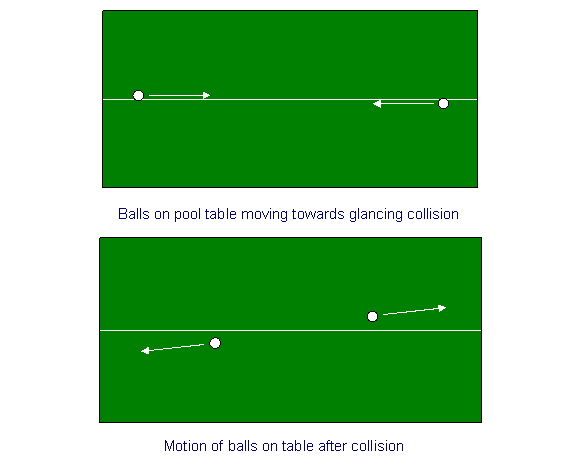
Une collision symétrique de vaisseaux spatiaux

Reprenons maintenant l’exercice à grande échelle. Supposons que quelque part dans l’espace, loin de tout champ gravitationnel, nous disposions une corde d’un million de kilomètres de long. (Elle pourrait se trouver entre nos deux horloges dans l’expérience de dilatation du temps). Cette corde correspond à la ligne de craie sur la table de billard. Supposons maintenant que deux vaisseaux spatiaux identiques s’approchent l’un de l’autre à des vitesses égales et opposées parallèlement à la corde depuis les deux extrémités de la corde, de sorte qu’ils subissent une légère collision rasante lorsqu’ils se rencontrent au milieu. Il est évident, du fait de la symétrie de la situation, que la quantité de mouvement est conservée dans les deux directions. En particulier, la vitesse à laquelle un vaisseau spatial s’éloigne de la ficelle après la collision – sa vitesse y – est égale et opposée à la vitesse à laquelle l’autre s’éloigne de la ficelle.

Mais maintenant, considérons cette collision telle qu’elle est observée par quelqu’un dans l’un des vaisseaux spatiaux, appelons-le A. Avant la collision, il voit la corde se déplacer très rapidement près de la fenêtre, disons à quelques mètres. Après la collision, il voit la corde s’éloigner, à une vitesse de 15 mètres par seconde. Cela s’explique par le fait que le vaisseau Ah a pris une vitesse perpendiculaire à la corde de 15 mètres par seconde. Pendant ce temps, comme il s’agit d’une situation complètement symétrique, un observateur sur le vaisseau spatial B déduirait certainement que son vaisseau spatial s’éloigne de la corde à 15 mètres par seconde également.

C’est symétrique à quel point ?

La question cruciale est : à quelle vitesse un observateur inspirant le vaisseau spatial A voit-il le vaisseau spatial B s’éloigner de la ficelle ? Supposons que par rapport au vaisseau spatial A, le vaisseau spatial B s’éloigne (dans la direction x) à 0,6c. Tout d’abord, rappelons que les distances perpendiculaires à la direction du mouvement ne sont pas contractées selon Lorentz. Par conséquent, lorsque l’observateur du vaisseau B dit qu’il s’est éloigné de 15 mètres de la corde dans un intervalle d’une seconde, l’observateur qui suit ce mouvement depuis le vaisseau A sera d’accord sur les 15 mètres, mais pas sur la seconde ! Il diraque ses horloges sont lentes, donc, mesuré par ses horloges, 1,25 seconde se sera écoulée pendant qu’elle se déplace de 15 mètres dans la direction y.

Il s’ensuit que, du fait de la dilatation du temps, cettecollision vue du vaisseau spatial A ne provoque pas des vitesses égales et opposées pour les deux vaisseaux spatiaux dans la direction y. Au départ, les deux vaisseaux spatiaux se déplaçaient parallèlement à l’axe x, il y avait un moment zéro dans la direction y. Alors comment peut-on affirmer qu’il y a une quantité de mouvement totale nulle dans la direction y après la collision, lorsque les vaisseaux spatiaux identiques n’ont pas des vitesses égales et opposées ?

Einstein sauve la conservation de la quantité de mouvement

Einstein était tellement sûr que la conservation de la quantité de mouvement doit toujours exister qu’il l’a sauvée avec une hypothèse audacieuse : la masse d’un objet doit dépendre de sa vitesse ! En fait, la masse doit augmenter avec la vitesse de manière à annuler la baisse de vitesse dans la direction y résultant de la dilatation du temps. C’est-à-dire que si un objet au repos a une masse m, en se déplaçant à une vitesse v il aura une inertie correspondant à une « masse relativiste » m rel =m/ 1-( v 2 / c 2 ) .Alors la quantité de mouvement devient

p → = m rel v → =m v → / 1-( v 2 / c 2 ) .

Notez que cette augmentation de masse relativiste est un effet indétectable et faible aux vitesses ordinaires, mais lorsqu’un objet s’approche de la vitesse de vol, la masse augmente sans limite !

La masse augmente vraiment avec la vitesse

Décider que les masses des objets doivent dépendre de la vitesse comme ceci semble un prix lourd à payer pour sauver la conservation de la quantité de mouvement ! Pourtant, il s’agit d’une prédiction qu’il n’est pas difficile de vérifier par l’expérience. La première confirmation a eu lieu en 1908, en déviant des électrons rapides dans un tube à vide. En fait, les électrons dans un tube TV couleur de l’ancien style ont environ un demi pour cent d’inertie de plus que les électrons au repos, et il faut en tenir compte dans le calcul des champs magnétiques utilisés pour les guider vers l’écran.

De façon beaucoup plus spectaculaire, dans les accélérateurs de particules modernes, des champs électriques très puissants sont utilisés pour accélérer les électrons, les protons et d’autres particules. On constate dans la pratique que ces particules ont besoin de forces de plus en plus grandes pour continuer à s’accélérer à mesure que l’on s’approche de la vitesse de la lumière. Par conséquent, la vitesse de la lumière est une limite de vitesse absolue naturelle. Les particules sont accélérées à des vitesses où leur masse relativiste est des milliers de fois supérieure à leur masse mesurée au repos, généralement appelée « masse au repos ».

…ou pas ?

En fait, il y a un débat continu parmi les physiciensconcernant ce concept de masse relativiste. Le débat est largement sémantique : personne ne doute que l’expression correcte de la quantité de mouvement d’une particule ayant une masse au repos m se déplaçant avec une vitesse v → est p → = m 1- v 2 / c 2 v → . Mais les physiciens des particules en particulier, dont beaucoup passent leur vie à mesurer avec une grande précision les masses au repos des particules, ne sont pas très enthousiastes à l’idée d’écrire cela sous la forme p → = m rel v → . Ils n’aiment pas l’idée d’une masse variable. D’une part, cela pourrait donner l’impression qu’en accélérant une particule se gonfle, ou du moins que sa structure interne se modifie d’une manière ou d’une autre. En fait, une particule relativiste subit simplement une contraction de Lorentz dans la direction du mouvement, comme toute autre chose. Elle passe d’une forme sphérique vers une forme de disque ayant le même rayon transversal.

Alors comment comprendre cette « augmentation de masse » ? Comme d’habitude, Einstein avait raison : il a remarqué que toute forme d’énergie possède de l’inertie. L’énergie cinétique elle-même a de l’inertie. Or, l' »inertie » est une propriété essentielle de la masse. L’autre propriété fondamentale de la masse est qu’elle exerce une attraction gravitationnelle. Est-ce le cas de cette énergie cinétique ? Pour connaître la réponse, considérez une sphère remplie de gaz. Elle génère à l’extérieur d’elle-même un champ gravitationnel à symétrie sphérique, dont la force est proportionnelle à la masse totale. Si nous chauffons maintenant le gaz, les particules de gaz auront cette masse (relativiste) accrue, correspondant à leur énergie cinétique accrue, et le champ gravitationnel externe aura augmenté proportionnellement. (Personne ne doute de cela.)

Donc la « masse relativiste » possède bien les deux propriétés fondamentales de la masse : l’inertie et l’attraction gravitationnelle. (Comme cela deviendra clair dans les cours suivants, cette masse relativiste n’est rien d’autre que l’énergie totale,la masse au repos elle-même étant maintenant considérée comme de l’énergie.)

À un niveau plus trivial, certains enseignants s’opposent à l’introduction de la masse relativiste parce qu’ils craignent que les étudiants supposent que l’énergie cinétique d’une particule en mouvement relativiste est juste 1 2 m v → 2 en utilisant la masse relativiste – ce n’est pas le cas, comme nous le verrons bientôt.

Note de bas de page : Pour tous ceux qui pourraient passer un jour à un traitement plus mathématiquement sophistiqué, il faut ajouter que la masse au repos joue un rôle important en tant qu’invariant lors du passage d’un cadre de référence à un autre, mais la « masse relativiste » utilisée ici n’est en réalité que la première composante (l’énergie) du vecteur énergie-momentum à quatre dimensions d’une particule, et n’est donc pas un invariant.

Énergie cinétique et masse pour les particules très rapides

Pensons à l’énergie cinétique d’une de ces particules voyageant près de la vitesse de la lumière. Rappelez-vous que dans un cours précédent, nous avons trouvé que l’énergie cinétique d’une masse ordinaire non relativiste (c’est-à-dire se déplaçant lentement) m était de 1 2 m v 2 . Pour ce faire, nous avons examiné le travail nécessaire pour la soulever à une certaine hauteur : nous avons dû exercer une force égale à son poids W pour la soulever à une hauteur h, le travail total effectué, ou l’énergie dépensée, étant la force x la distance, Wh. En redescendant, la force de gravité, W, a exercé un travail exactement égal à Wh sur l’objet qui tombait, mais cette fois, le travail a servi à accélérer l’objet, à lui donner de l’énergie cinétique. Comme nous connaissons la vitesse de récupération des objets en chute, nous avons pu conclure que l’énergie cinétique était de 1 2 m v 2 . (Pour plus de détails, voir le cours précédent.)

De manière plus générale, nous aurions pu accélérer la masse avec une force F constante quelconque, et trouver le travail effectué par la force (force xdistance) pour l’amener à la vitesse v à partir d’un départ arrêté. L’énergie cinétique de la masse, E= 1 2 m v 2 , est exactement égale au travail effectué par la force pour amener la masse à cette vitesse. (On peut montrer de façon similaire que si une force est appliquée à une particule se déplaçant déjà à la vitesse u, disons, et qu’elle est accélérée jusqu’à la vitesse v, le travail nécessaire est de 1 2 m v 2 – 1 2 m u 2. )

Il est intéressant d’essayer de répéter l’exercice pour une particule se déplaçant très près de la vitesse de la lumière, comme les particules dans les accélérateurs mentionnés dans le paragraphe précédent. La deuxième loi de Newton, sous la forme

Force = taux de changement de la quantité de mouvement

est toujours vraie, mais près de la vitesse de la lumière, la vitesse change de façon négligeable alors que la force continue à agir – au lieu de cela, la masse augmente ! Par conséquent, nous pouvons écrire, avec une excellente approximation,

Force = (taux de changement de la masse) x c

où, comme d’habitude, c est la vitesse de la lumière. Pour être plus précis, supposons que nous ayons une force constante F qui pousse une particule. A un certain instant, la particule a une masse M, et une vitesse extrêmement proche de c. Une seconde plus tard, puisque la force continue à travailler sur la particule, et donc augmente son élan d’après la deuxième loi de Newton, la particule aura une masse M+m disons, où m est l’augmentation de la masse suite au travail effectué par la force.

Quel est l’accroissement de l’énergie cinétique E de la particule pendant cette période d’une seconde ? Par analogie exacte avec le cas non relativiste examiné ci-dessus, c’est juste le travail effectué par la force pendant cette période. Maintenant, puisque la masse de la particule change de m en une seconde, m est également le taux de changement de la masse. Par conséquent, à partir de la deuxième loi de Newton sous la forme

Force = (taux de changement de masse) x c,

on peut écrire

Force =mc.

L’augmentation de l’énergie cinétique E pendant la période d’une seconde est juste le travail effectué par la force,

E= force x distance.

Puisque la particule se déplace essentiellement à la vitesse du vol, la distance sur laquelle la force agit pendant la période d’une seconde est juste de c mètres, c=3× 10 8 .

Donc le travail total que la force effectue dans cette seconde est force xdistance =mc×c=m c 2 .

Donc la relation entre l’augmentation de la masse de la particule thélativiste et son augmentation d’énergie cinétique est :

E=m c 2 .

Énergie cinétique et masse pour les particules lentes

Rappelons que pour que les lois de Newton soient vraies dans tous les cadres inertiels, nous avons dû supposer une augmentation de la masse avec la vitesse par le facteur 1/ 1-( v 2 / c 2 ) . Cela implique que même un objet qui se déplace lentement a une minuscule augmentation de masse lorsqu’il se déplace !

Comment cette minuscule augmentation se rapporte-t-elle à l’énergie cinétique ? Considérons une masse M, se déplaçant à la vitesse v, bien inférieure à la vitesse de la lumière. Son énergie cinétique E= 1 2 M v 2 , comme nous l’avons vu plus haut. Sa masse est M/ 1-( v 2 / c 2 ), que nous pouvons écrire M+m. Quelle est la valeur de m ?

Puisque nous parlons de vitesses qui nous sont familières, comme un avion à réaction, où v/c, est vraiment petit, nous pouvons utiliser quelques astuces mathématiques simples pour faciliter les choses.

Le premier est une bonne approximation pour la racine carrée de 1-x lorsque x est beaucoup moins que un:

1-x ≅1- 1 2 x pour x≪1.

Vous pouvez facilement vérifier cela avec votre calculatrice : essayez x= 1 100 , vous trouvez 99 100 =0,994987… ce qui est extrêmement proche de 1- 1 2 1 100 =0,995 !

L’approximation suivante est

1 1-x ≅1+x pour x≪1.

Cela est également facile à vérifier : prenons à nouveau x= 1 100 : 1 1-x = 1 99 100 = 100 99 =1,01010… ,et 1+x= 101 100 =1,01.

En utilisant ces approximations avec x=v/c, on peut approximer 1-( v 2 / c 2 ) comme 1- 1 2 ( v 2 / c 2 ) ,puis 1/( 1- 1 2 ( v 2 / c 2 ) ) comme 1+ 1 2 ( v 2 / c 2 ) .

Cela signifie que la masse totale à la vitesse v

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ),

et en écrivant ceci comme M+m, nous voyons que l’augmentation de masse m est égale à 1 2 M v 2 / c 2 .

Cela signifie que – encore une fois – l’augmentation de masse m est liée à l’énergie cinétique E par E=m c 2 .

En fait, il n’est pas difficile de montrer, en utilisant un peu de calcul, que sur toute la gamme de vitesse allant de zéro à aussi près que vous le souhaitez de la vitesse de la lumière, une particule en mouvement connaît une augmentation de masse liée à son énergie cinétique par E=m c 2 . Pour comprendre pourquoi on ne s’en aperçoit pas dans la vie de tous les jours, prenez l’exemple d’un avion à réaction pesant 100 tonnes et se déplaçant à 2 000 mph. 100 tonnes, c’est 100 000 kilogrammes, 2 000 mph, c’est environ 1 000 mètres par seconde. C’est une énergie cinétique 1 2 M v 2 de ½ ×1011joules, mais le changement de masse correspondant de l’avion vers le bas par le facteur c 2 , 9× 10 16 , donnant une augmentation de masse réelle d’environ un demi-milligramme, pas trop facile à détecter !

E = mc2

Nous avons vu ci-dessus que lorsqu’une force effectue un travail accélérant un corps pour lui donner de l’énergie cinétique, la masse du corps augmente d’une quantité égale au travail total effectué par la force, l’énergie E transférée, divisée par c 2 . Qu’en est-il lorsqu’une force exerce sur un corps un travail qui ne l’accélère pas, de sorte qu’il n’y a pas d’augmentation de l’énergie cinétique ? Par exemple, que se passe-t-il si je ne fais que soulever quelque chose à une vitesse constante, en lui donnant de l’énergie potentielle ? Il s’avère que dans ce cas aussi, il y a une augmentation de la masse donnée par E=m c 2 , bien sûr non mesurable pour les objets de tous les jours.

Cependant, c’est un effet mesurable et important en physique nucléaire. Par exemple, l’atome d’hélium a un noyau qui comporte deux protons et deux neutrons liés entre eux de manière très étanche par une forte force d’attraction nucléaire. Si une force extérieure suffisante est appliquée, ce noyau peut être séparé en deux noyaux d' »hydrogène lourd », chacun ayant un proton et un neutron. Une grande quantité d’énergie extérieure doit être dépensée pour réaliser cette séparation, et l’on constate que la masse totale des deux noyaux d’hydrogène lourd est sensiblement (environ un demi pour cent) plus lourde que le noyau d’hélium initial. Cette extramasse, multipliée par c 2 , est juste égale à l’énergie nécessaire pour séparer le noyau d’hélium en deux. Plus important encore, cette énergie peut être récupérée en laissant les deux noyaux d’hydrogène lourds entrer en collision et se réunir pour former à nouveau un noyau d’hélium. (Ils sont tous deux chargés électriquement de manière positive, ils se repoussent donc l’un l’autre, et doivent se rapprocher assez rapidement pour surmonter cette répulsion et atteindre la proximité où l’attraction nucléaire, beaucoup plus forte, entre en jeu). C’est la source d’énergie de base de la bombe à hydrogène, et du soleil.

Il s’avère que toutes les formes d’énergie, cinétique et différentes sortes d’énergie potentielle, ont une masse associée donnée par E=m c 2 . Pour les réactions nucléaires, le changement de masse est typiquement de l’ordre du millième de la masse totale, et facilement mesurable. Pour les réactions chimiques, le changement est de l’ordre du milliardième de la masse totale, et n’est pas actuellement mesurable.

index précédent

.