La définition suivante des statistiques robustes provient du livre de P. J. Huber, Robust Statistics.
… toute procédure statistique devrait posséder les caractéristiques souhaitables suivantes :
- Elle devrait avoir une efficacité raisonnablement bonne (optimale ou presque optimale) au modèle supposé.
- Elle devrait être robuste dans le sens où de petits écarts par rapport aux hypothèses du modèle ne devraient altérer que légèrement la performance. …
- Des écarts un peu plus importants par rapport au modèle ne devraient pas provoquer de catastrophe.
La statistique classique se concentre sur le premier des points de Huber, produisant des méthodes qui sont optimales sous réserve de certains critères. Ce post examine les exemples canoniques utilisés pour illustrer les deuxième et troisième points de Huber.
Le troisième point de Huber est généralement illustré par la moyenne de l’échantillon (moyenne) et la médiane de l’échantillon (valeur moyenne). Vous pouvez fixer près de la moitié des données d’un échantillon à ∞ sans que la médiane de l’échantillon devienne infinie. La moyenne de l’échantillon, en revanche, devient infinie si toute valeur de l’échantillon est infinie. De grands écarts par rapport au modèle, c’est-à-dire quelques valeurs aberrantes, pourraient provoquer une catastrophe pour la moyenne de l’échantillon mais pas pour la médiane de l’échantillon.
L’exemple canonique lors de la discussion du deuxième point de Huber remonte à John Tukey. Commencez par l’exemple d’estimation le plus simple du manuel : des données provenant d’une distribution normale avec une moyenne inconnue et une variance 1, c’est-à-dire que les données sont normales(μ, 1) avec μ inconnu. La façon la plus efficace d’estimer μ est de prendre la moyenne de l’échantillon, la moyenne des données.
Mais supposons maintenant que la distribution des données n’est pas exactement normale(μ, 1) mais plutôt un mélange d’une distribution normale standard et d’une distribution normale avec une variance différente. Laissez δ être un petit nombre, disons 0,01, et supposez que les données proviennent d’une distribution normale(μ, 1) avec une probabilité de 1-δ et que les données proviennent d’une distribution normale(μ, σ2) avec une probabilité de δ. Cette distribution est appelée une « normale contaminée » et le nombre δ est la quantité de contamination. La raison de l’utilisation du modèle normal contaminé est que c’est une distribution non normale qui peut sembler normale à l’œil.
Nous pourrions estimer la moyenne de la population μ en utilisant soit la moyenne de l’échantillon, soit la médiane de l’échantillon. Si les données étaient strictement normales plutôt qu’un mélange, la moyenne d’échantillon serait l’estimateur le plus efficace de μ. Dans ce cas, l’erreur standard serait environ 25% plus grande si nous utilisions la médiane d’échantillon. Mais si les données proviennent bien d’un mélange, la médiane de l’échantillon peut être plus efficace, en fonction des tailles de δ et σ. Voici un graphique de l’ARE (efficacité relative asymptotique) de la médiane de l’échantillon par rapport à la moyenne de l’échantillon en fonction de σ lorsque δ = 0.01.
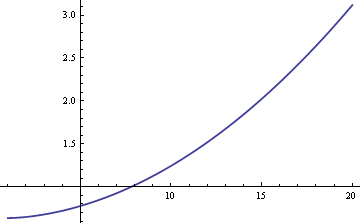
Le tracé montre que pour des valeurs de σ supérieures à 8, la médiane de l’échantillon est plus efficace que la moyenne de l’échantillon. La supériorité relative de la médiane croît sans limite lorsque σ augmente.
Voici un tracé de l’ARE avec σ fixé à 10 et δ variant entre 0 et 1.
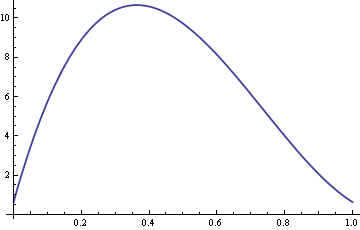
Donc pour des valeurs de δ autour de 0.4, la médiane de l’échantillon est plus de dix fois plus efficace que la moyenne de l’échantillon.
La formule générale de l’ARE dans cet exemple est 2((1 + δ(σ2 – 1)(1 – δ + δ/σ)2)/ π.
Si vous êtes sûr que vos données sont normales sans contamination ou avec une contamination très faible, alors la moyenne de l’échantillon est l’estimateur le plus efficace. Mais il peut être intéressant de risquer de renoncer à un peu d’efficacité en échange de savoir que vous ferez mieux avec un modèle robuste en cas de contamination importante. Il y a plus de potentiel de perte en utilisant la moyenne de l’échantillon lorsqu’il y a une contamination significative que de gain potentiel en utilisant la moyenne de l’échantillon lorsqu’il n’y a pas de contamination.
Voici une énigme associée à l’exemple de la normale contaminée. L’estimateur le plus efficace pour les données normales(μ, 1) est la moyenne de l’échantillon. Et l’estimateur le plus efficace pour les données normales(μ, σ2) est également de prendre la moyenne de l’échantillon. Alors pourquoi n’est-il pas optimal de prendre la moyenne d’échantillon du mélange ?
La clé est que nous ne savons pas si un échantillon particulier provient de la distribution normale(μ, 1) ou de la distribution normale(μ, σ2). Si nous le savions, nous pourrions séparer les échantillons, en faire la moyenne séparément, et combiner les échantillons en une moyenne agrégée : multiplier une moyenne par 1-δ, multiplier l’autre par δ, et ajouter. Mais comme nous ne savons pas quels composants du mélange conduisent à quels échantillons, nous ne pouvons pas peser les échantillons de manière appropriée. (Nous ne connaissons probablement pas non plus δ, mais c’est une autre question.)
Il existe d’autres options que l’utilisation de la moyenne ou de la médiane de l’échantillon. Par exemple, la moyenne tronquée jette certaines des valeurs les plus grandes et les plus petites puis fait la moyenne de tout le reste. (Les sports fonctionnent parfois de cette manière, en éliminant les notes les plus élevées et les plus basses d’un athlète par les juges). Plus le nombre de données rejetées est important, plus la moyenne ajustée se comporte comme la médiane de l’échantillon. Moins il y a de données jetées, plus elle se comporte comme la moyenne de l’échantillon.
Poste connexe : Efficacité de la médiane par rapport à la moyenne pour les distributions Student-t
Pour des conseils quotidiens sur la science des données, suivez @DataSciFact sur Twitter.
.