Trouver les sources : « Norme uniforme » – actualité – journaux – livres – érudit – JSTOR (décembre 2009) (Learn how and when to remove this template message)
En analyse mathématique, la norme uniforme (ou sup norm) attribue aux fonctions f bornées à valeurs réelles ou complexes définies sur un ensemble S le nombre non négatif
‖ f ‖ ∞ = ‖ f ‖ ∞ , S = sup { | f ( x ) | : x ∈ S } . . {\displaystyle \|f\|{{{infty}=\|f\|{{infty ,S}=\sup \left\{{\i},\left|f(x)\right|:x\in S\,\right\}.} 
Cette norme est également appelée norme du supremum, norme de Chebyshev, norme de l’infini, ou, lorsque le supremum est en fait le maximum, la norme max. Le nom « norme uniforme » provient du fait qu’une séquence de fonctions { f n } {\displaystyle \{f_{n}}} 



La métrique engendrée par cette norme est appelée métrique de Tchebychev, du nom de Pafnuty Tchebychev, qui fut le premier à l’étudier systématiquement.
Si l’on admet des fonctions non bornées, cette formule ne donne pas une norme ou une métrique au sens strict, bien que la métrique dite étendue obtenue permette encore de définir une topologie sur l’espace de fonctions en question.
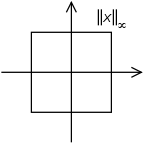
Si f est une fonction continue sur un intervalle fermé, ou plus généralement un ensemble compact, alors elle est bornée et le supremum dans la définition ci-dessus est atteint par le théorème des valeurs extrêmes de Weierstrass, on peut donc remplacer le supremum par le maximum. Dans ce cas, la norme est aussi appelée norme maximale.En particulier, pour le cas d’un vecteur x = ( x 1 , … , x n ) {\displaystyle x=(x_{1},\dots ,x_{n})} 
‖ x ‖ ∞ = max { | x 1 | , … , | x n | }. . {\displaystyle \|x\\_{{\i1}}=\max\{|x_{1}|,\dots ,|x_{n}|\}.}
La raison de l’indice « ∞ » est que chaque fois que f est continue
lim p → ∞ ‖ f ‖ p = ‖ f ‖ ∞ , {\displaystyle \lim _{p\rightarrow \infty }\|f\|_{p}=\|f\|_{\infty },} 
où
‖ f ‖ p = ( ∫ D | f | p d μ ) 1 / p {\displaystyle \|f\|_{p}=\left(\int _{D}\left|f\right|^{p}\,d\mu \right)^{1/p}} 
où D est le domaine de f (et l’intégrale se résume à une somme si D est un ensemble discret).
La fonction binaire
d ( f , g ) = ‖ f – g ‖ ∞ {\displaystyle d(f,g)=\|f-g\|_{\infty }}. 
est alors une métrique sur l’espace de toutes les fonctions bornées (et, évidemment, n’importe lequel de ses sous-ensembles) sur un domaine particulier. Une séquence { fn : n = 1, 2, 3, … } converge uniformément vers une fonction f si et seulement si
lim n → ∞ ‖ f n – f ‖ ∞ = 0. {\displaystyle}\lim _{n\rightarrow \infty }\|f_{n}-f\|{\infty }=0.\,} 
Nous pouvons définir les ensembles fermés et les fermetures d’ensembles par rapport à cette topologie métrique ; les ensembles fermés dans la norme uniforme sont parfois appelés uniformément fermés et les fermetures uniformes. La fermeture uniforme d’un ensemble de fonctions A est l’espace de toutes les fonctions qui peuvent être approximées par une séquence de fonctions uniformément convergentes sur A. Par exemple, une reformulation du théorème de Stone-Weierstrass est que l’ensemble de toutes les fonctions continues sur {\displaystyle } 

Pour les fonctions continues complexes sur un espace compact, cela le transforme en une algèbre C*.
.