Alai

Programmes d’automates

Les automates de différents fabricants peuvent être programmés de différentes manières. Les langages de programmation populaires pour les automates sont les diagrammes en échelle, les diagrammes de blocs fonctionnels (FBD) et les listes d’instructions. À quelques exceptions près, un programme écrit dans un format peut être visualisé dans un autre.

Langages de programmation populaires pour les automates

Prenons la discussion sur chacun des langages de programmation populaires pour les automates :

1. Diagrammes Ladder
   • Exemple
   • Cours vidéo (bases du diagramme Ladder)
2. Diagramme à blocs fonctionnels
   • Cours vidéo (programmation du diagramme à blocs fonctionnels (FBD))
3. Liste d’énoncés
   • Cours vidéo (comment utiliser PLCSIM S7-.300 STL)
4. Fonctions logiques
   • Cours vidéo (Portes logiques vs Circuits logiques Ladder)

1. Diagrammes Ladder

En guise d’introduction au diagramme Ladder, considérons le circuit simple d’un relais qui contient une bobine et des contacts comme indiqué sur la figure 1.

Lorsqu’une tension est appliquée à la bobine d’entrée, le courant résultant crée un champ magnétique. Le champ magnétique attire un interrupteur métallique (ou reed) vers lui et les contacts se touchent, fermant l’interrupteur. Le contact qui se ferme lorsque la bobine est alimentée est appelé normalement ouvert (NO).

Les contacts normalement fermés (NC) se touchent lorsque la bobine d’entrée n’est pas alimentée. Lorsque la bobine d’entrée n’est pas alimentée, les contacts normalement fermés seront fermés (conducteurs).

L’agencement du relais peut être représenté à l’aide de différents circuits schématiques comme le montre la figure 1.

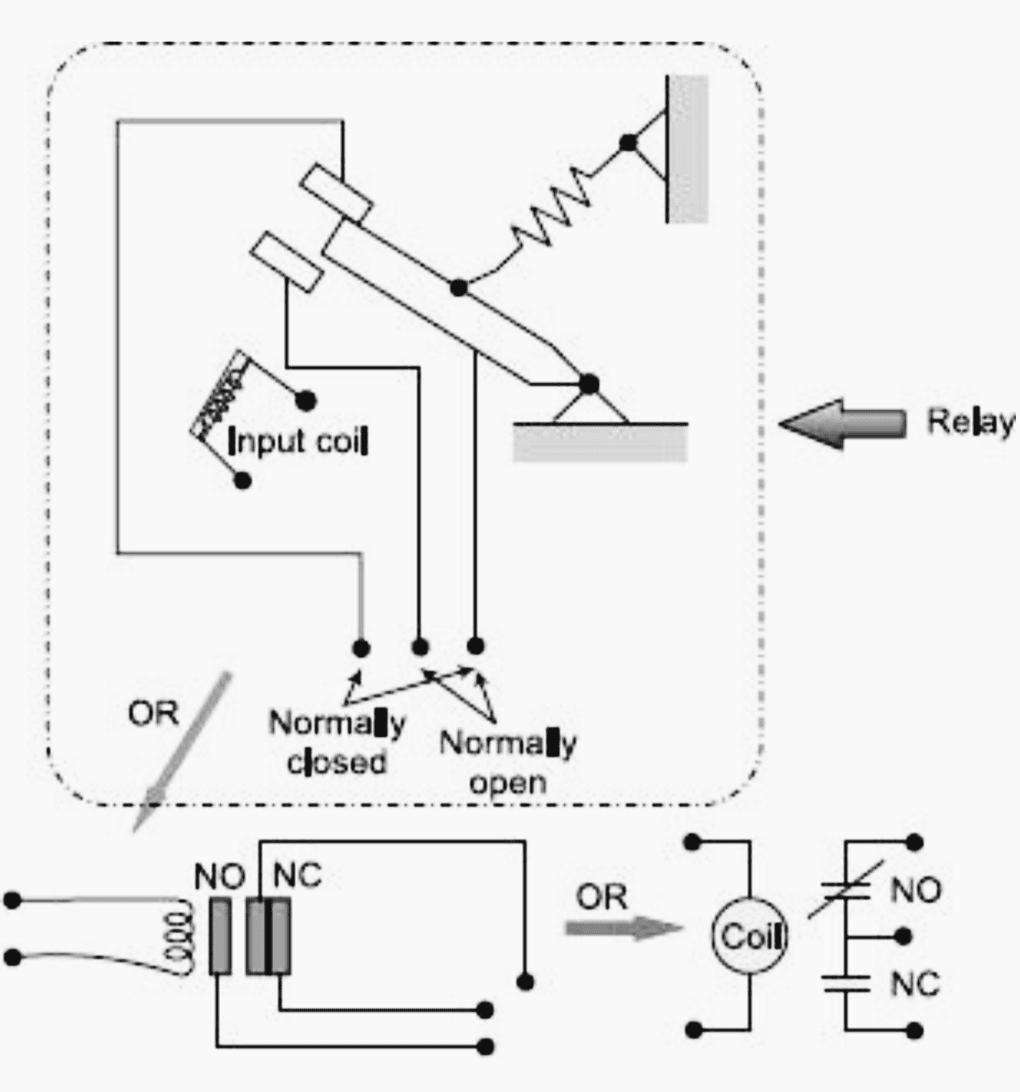
Les relais sont normalement dessinés sous forme de schéma en utilisant un cercle pour représenter la bobine d’entrée. Les contacts de sortie sont représentés par deux lignes parallèles. Les contacts NO sont représentés par deux lignes, et seront ouverts (non conducteurs) lorsque l’entrée n’est pas alimentée. Les contacts NC sont représentés par deux lignes traversées par une ligne diagonale.

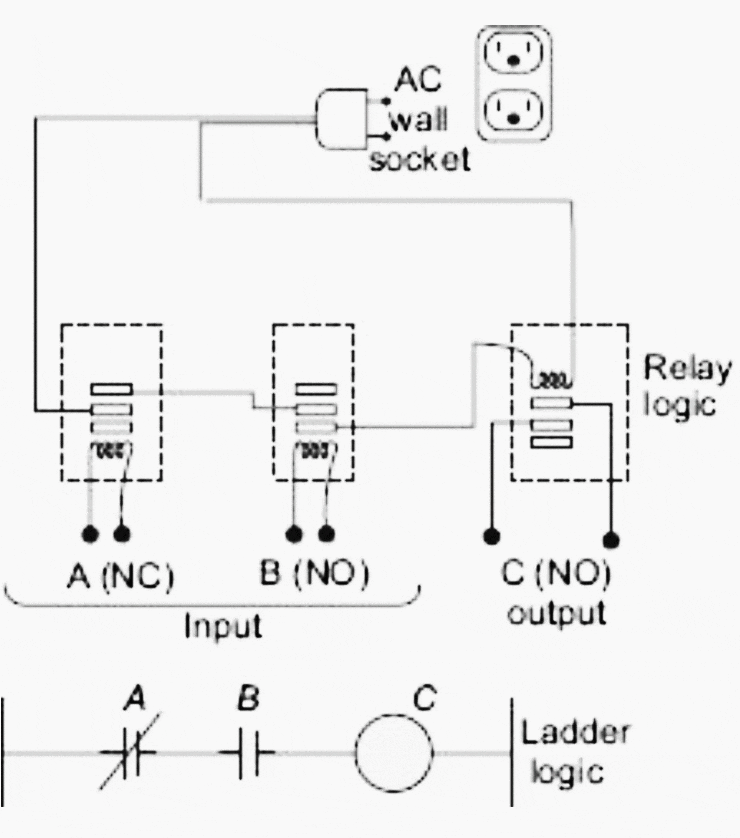
Maintenant, s’il est nécessaire de faire fonctionner le contact NO (C) de ce relais, connecté à une source de courant alternatif, par l’intermédiaire de deux contacts de relais d’entrée, A (NC) et B (NO), alors le diagramme logique de relais présenté à la figure 2 est le plus approprié pour une logique typique.

Selon le diagramme logique de relais présenté sur la figure, l’activation de la bobine du relais d’entrée correspond au contact B, fait que C (sortie) se ferme et l’activation de la bobine du relais d’entrée correspond au contact A, fait que C (sortie) s’ouvre.

Ce genre d’arrangement est normalement employé dans un circuit logique de relais conventionnel câblé.

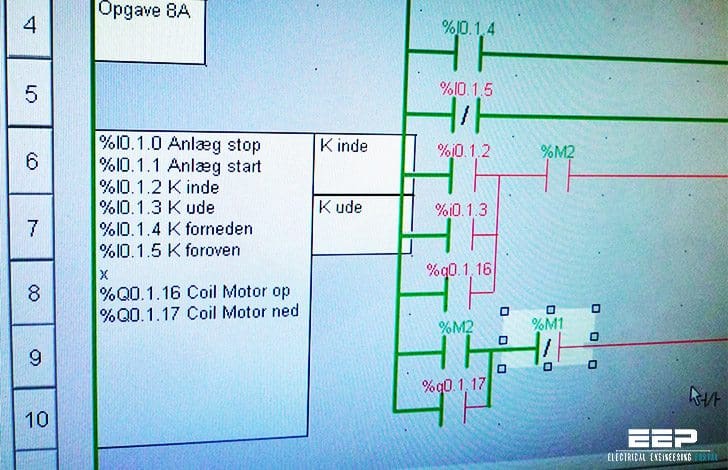
Le même schéma peut être mis en œuvre en suivant la logique en échelle comme le montre la figure 2. Le diagramme logique en échelle est la méthode la plus couramment utilisée pour programmer les automates. Le diagramme en échelle est constitué de deux lignes verticales représentant les rails d’alimentation. Les circuits connectés sous forme de lignes horizontales entre deux rails sont appelés barreaux de l’échelle. Quelques symboles utilisés pour désigner les entrées et les sorties de la logique en échelle sont présentés dans les figures 3 et 4 respectivement.

En tenant compte de ces symboles de logique en échelle, la logique en échelle mise en œuvre dans la figure 2 imite la même logique de relais câblée.

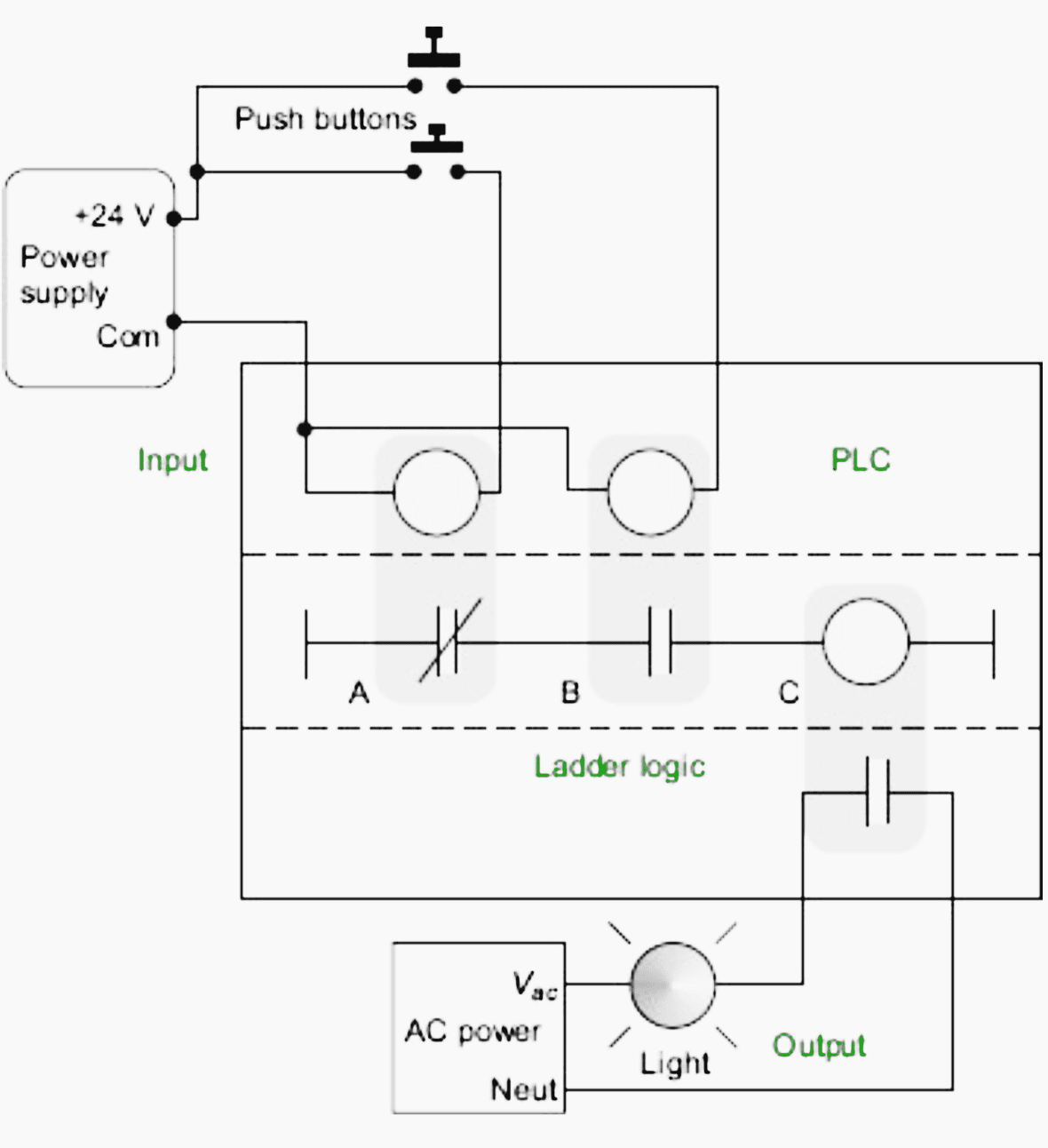
Enfin, cette logique en échelle est insérée en tant que programme de commande dans un PLC où, les dispositifs d’entrée, et les dispositifs de sortie sont disposés de la manière illustrée dans la figure 5.

Donc, les programmes de logique en échelle sont chargés dans l’automate, les dispositifs d’entrée et de sortie sont connectés aux modules d’entrée/sortie, puis l’exécution du programme met à jour les sorties en fonction de l’état des entrées.

De nombreux relais ont également plusieurs sorties et cela permet à un relais de sortie d’être également une entrée simultanément.

Le circuit illustré à la figure 6 en est un exemple et il est appelé circuit à scellement. Dans ce circuit, le courant peut circuler dans l’une ou l’autre des branches du circuit, à travers les contacts étiquetés A ou B.

Note ! Si A est fermé, la sortie B s’allume, et l’entrée B s’allume également, ce qui maintient la sortie B en permanence – jusqu’à ce que l’alimentation soit coupée.

Un autre exemple de logique en échelle peut être vu dans la figure 7. Pour interpréter ce schéma, imaginez que l’alimentation se trouve sur la ligne verticale du côté gauche, appelée rail chaud. Du côté droit se trouve le rail neutre.

Une sortie sera un dispositif extérieur à l’automate qui est allumé ou éteint, comme des lumières ou des moteurs. Dans l’échelon supérieur, les contacts sont normalement ouverts et normalement fermés, ce qui signifie que si l’entrée A est activée et que l’entrée B est désactivée, alors le courant circulera dans la sortie et l’activera.

Toute autre combinaison de valeurs d’entrée entraînera la désactivation de la sortie X.

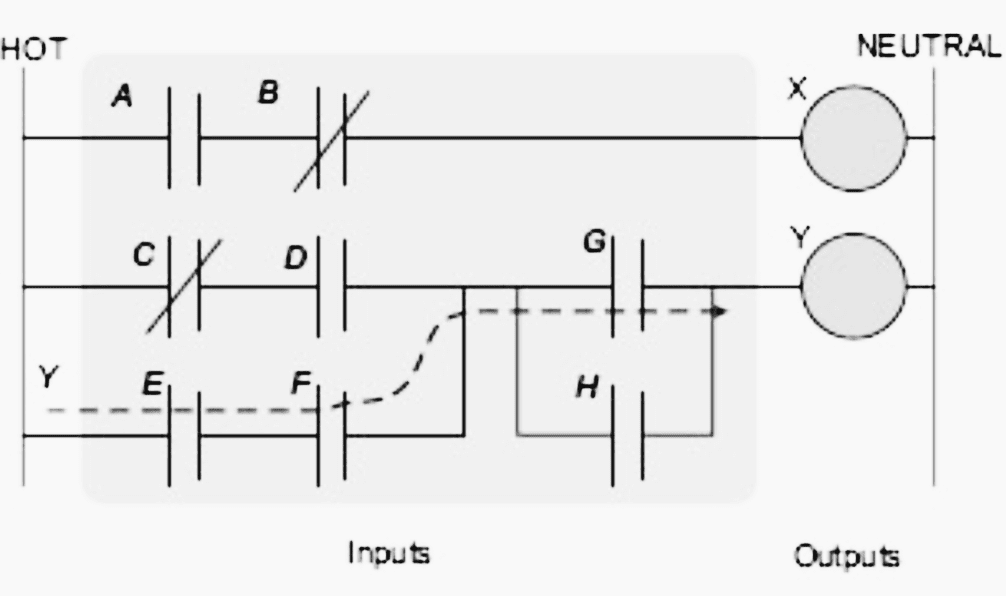
Note ! Le courant doit passer par une certaine combinaison des entrées (A, B, C, D, E, F, G et H) pour allumer les sorties (X, Y)

Retournez au sommaire

Exemple //

Essayez de développer (sans regarder la solution) un contrôleur à base de relais qui permettra à trois interrupteurs dans une pièce de contrôler une seule lumière.

Solution

Il y a deux approches possibles à ce problème. La première suppose que n’importe lequel des interrupteurs allumés allume la lumière, mais que les trois interrupteurs doivent être éteints pour que la lumière soit éteinte. La logique en échelle est présentée dans la figure 8.

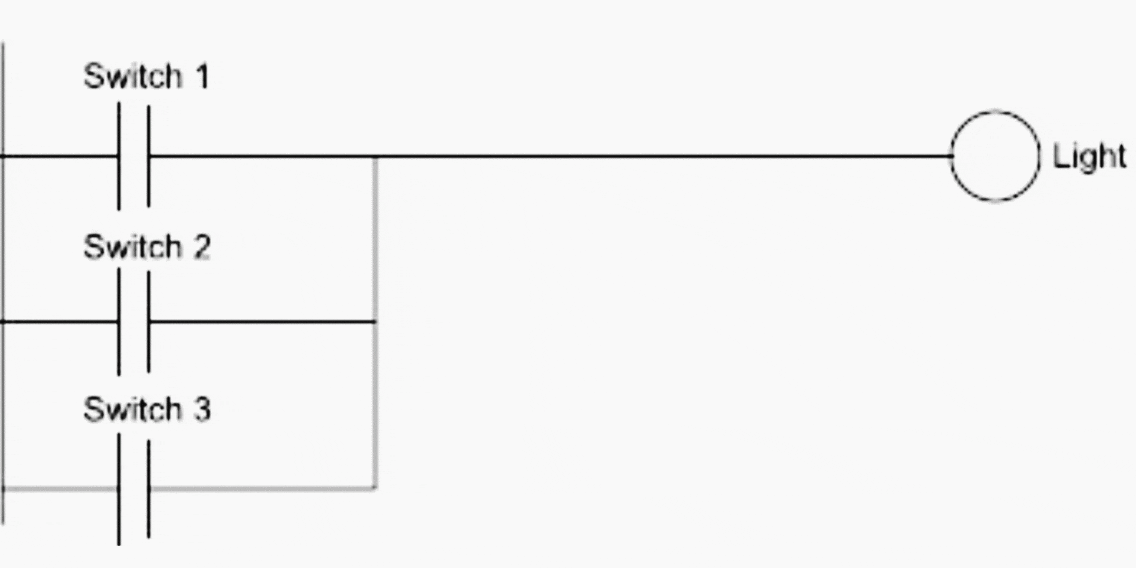
La deuxième solution suppose que chaque interrupteur peut allumer ou éteindre la lumière, indépendamment des états des autres interrupteurs. Cette méthode est plus complexe et implique de réfléchir à toutes les combinaisons possibles de positions d’interrupteurs.

Vous pourriez reconnaître ce problème comme un problème exclusif ou. La logique en échelle est telle que présentée dans la figure 9.

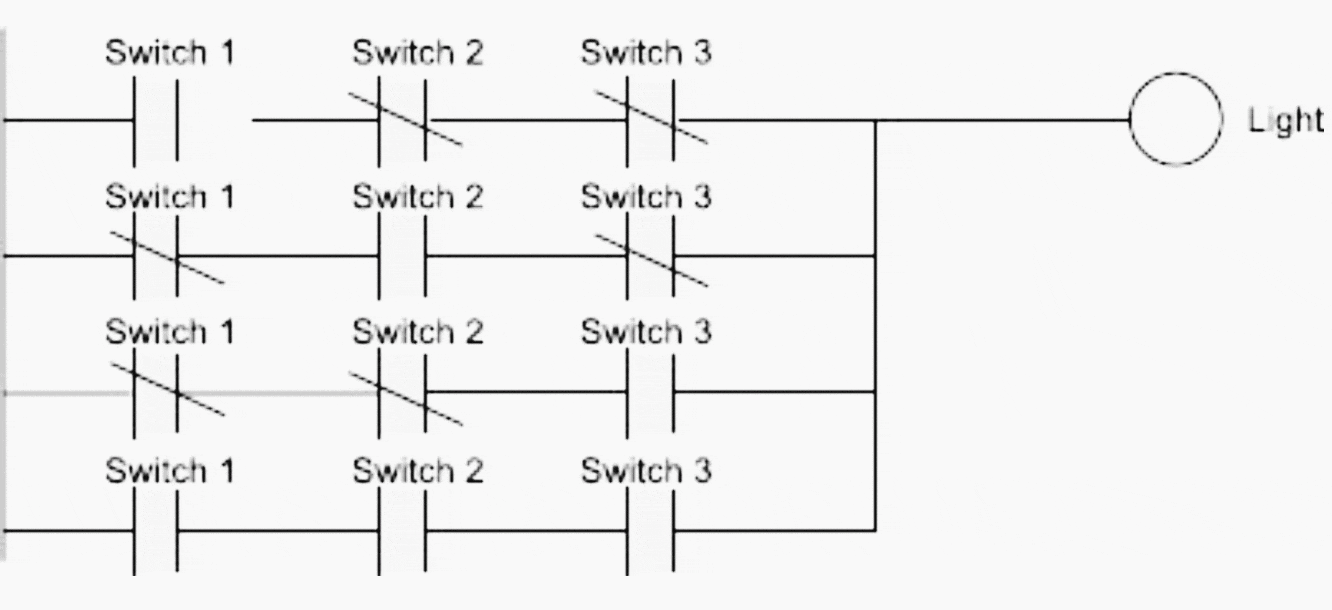
Note ! Il est important de bien comprendre comment les commandes sont censées fonctionner. Dans cet exemple, deux solutions radicalement différentes ont été obtenues sur la base d’une simple différence de fonctionnement.

Voir le sommaire

Bases du diagramme en échelle #1

Bases du diagramme en échelle #2 (circuit de commande de sécurité)

Bases du diagramme en échelle #3 (circuit de commande de moteur à 2 fils & 3 fils)

Voir le sommaire

2. Diagramme de bloc fonctionnel

Le diagramme de bloc fonctionnel (FBD) est utilisé pour les programmes d’automates décrits en termes de blocs graphiques. Il est décrit comme étant un langage graphique permettant de représenter les flux de signaux et de données à travers des blocs d’entrées, ceux-ci étant des éléments logiciels réutilisables.

Les blocs fonctionnels peuvent avoir des fonctions standard, comme celles des portes logiques ou des compteurs ou des temporisateurs, ou avoir des fonctions définies par l’utilisateur, par exemple un bloc pour obtenir une valeur moyenne des entrées.

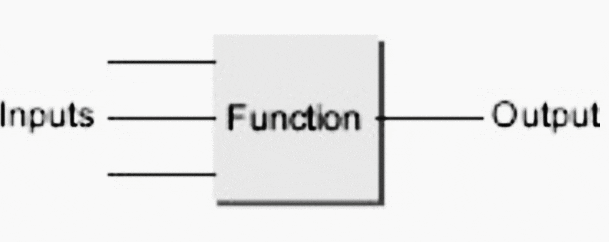
Retour au sommaire

Programmation par diagramme à blocs fonctionnels (FBD) – Première leçon

Dans cette vidéo, vous apprendrez les bases de la programmation des automates avec le langage de diagramme à blocs fonctionnels (FBD). FBD est un langage graphique, dans lequel vous traitez les blocs et la connexion entre les blocs.

Comment créer et utiliser les blocs fonctionnels dans le projet

Dans cette vidéo, vous apprendrez comment créer des blocs fonctionnels personnalisés dans le projet et les appeler dans le programme principal.

Retourner au sommaire

3. Liste d’énoncés

Dans l’approche de programmation par liste d’énoncés, un jeu d’instructions similaire au langage d’assemblage pour un microprocesseur est utilisé. Les listes d’énoncés, disponibles sur quelques marques d’automates, constituent la forme de programmation la plus flexible pour l’utilisateur expérimenté, mais ne sont en aucun cas aussi faciles à suivre que les diagrammes en échelle ou les symboles logiques.

La figure 11 montre une opération simple sous forme de diagramme en échelle pour un automate Mistsubishi. La liste d’instructions équivalente serait celle présentée dans le tableau 1.

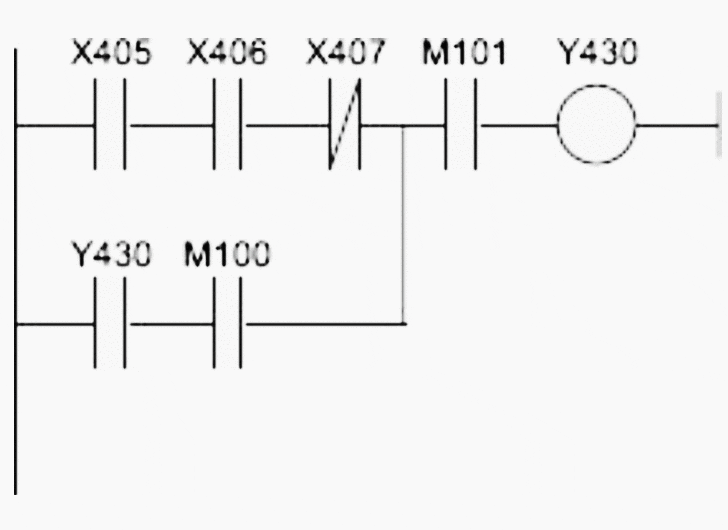
Retour au sommaire

Comment utiliser PLCSIM S7-…300 STL LESSON 1 Tutorial

Dans cette leçon, nous discutons du programme STL et du concept de RLO&STA. Des informations détaillées sur RLO et STA sont expliquées ainsi que la simulation.

PLCSIM S7 300 STL LESSON 2 Tutoriel…l’automatisation dans l’usine

Dans cette leçon, nous apprendrons à écrire un programme PLC en utilisant un PLC « S7 300 » et le logiciel « STEP 7 ».

Retourner au sommaire

4. Fonctions logiques

Il existe de nombreuses situations de commande nécessitant le déclenchement d’actions lorsqu’une certaine combinaison de conditions est réalisée. Ainsi, pour une perceuse automatique, il peut y avoir une condition selon laquelle le moteur de la perceuse doit être activé lorsque des interrupteurs de fin de course sont activés qui indiquent la présence de la pièce à usiner et la position de la perceuse comme étant à la surface de la pièce à usiner.

Le circuit électrique, la table de vérité, le diagramme en échelle et le diagramme de bloc fonctionnel pour différentes logiques sont présentés dans le tableau 2.

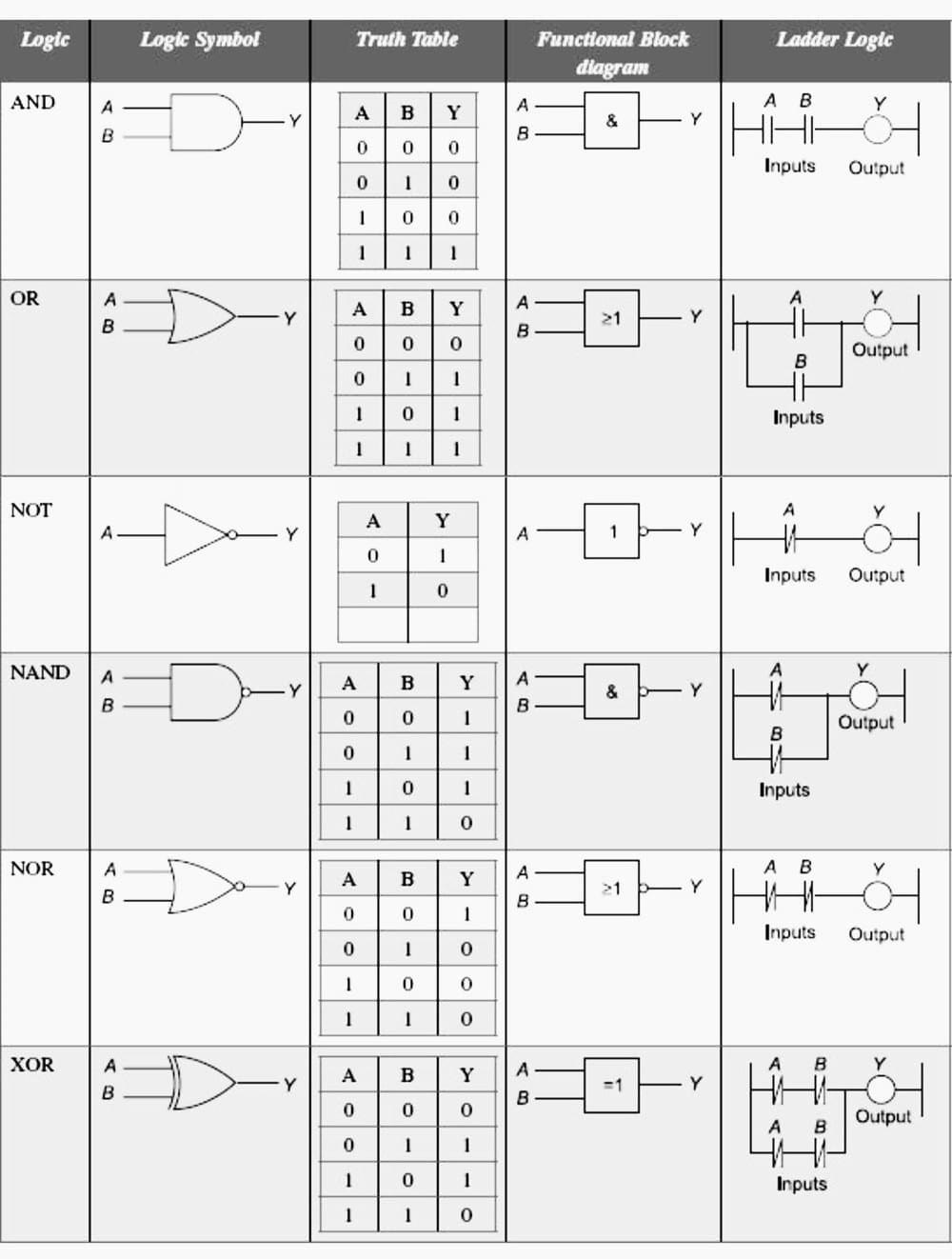
Retournez au sommaire

Portes logiques contre circuits logiques en échelle

Retournez au sommaire

.