Alai

Par Raymond Yuan, Stagiaire en génie logiciel

Dans ce tutoriel, nous allons apprendre à utiliser l’apprentissage profond pour composer des images dans le style d’une autre image (vous avez déjà souhaité peindre comme Picasso ou Van Gogh ?). C’est ce qu’on appelle le transfert de style neuronal ! C’est une technique décrite dans l’article de Leon A. Gatys, A Neural Algorithm of Artistic Style, qui est une excellente lecture et que vous devriez absolument consulter.

Le transfert de style neuronal est une technique d’optimisation utilisée pour prendre trois images, une image de contenu, une image de référence de style (telle qu’une œuvre d’art d’un peintre célèbre) et l’image d’entrée que vous voulez styliser – et les mélanger ensemble de sorte que l’image d’entrée soit transformée pour ressembler à l’image de contenu, mais « peinte » dans le style de l’image de style.

Par exemple, prenons une image de cette tortue et La grande vague au large de Kanagawa de Katsushika Hokusai :

Mais à quoi cela ressemblerait-il si Hokusai décidait d’ajouter la texture ou le style de ses vagues à l’image de la tortue ? Quelque chose comme ça ?

C’est de la magie ou du deep learning ? Heureusement, cela n’implique aucune magie : le transfert de style est une technique amusante et intéressante qui met en valeur les capacités et les représentations internes des réseaux neuronaux.

Le principe du transfert de style neuronal consiste à définir deux fonctions de distance, l’une qui décrit la différence entre le contenu de deux images, Lcontent, et l’autre qui décrit la différence entre les deux images en termes de style, Lstyle. Ensuite, étant donné trois images, une image de style désirée, une image de contenu désirée, et l’image d’entrée (initialisée avec l’image de contenu), nous essayons de transformer l’image d’entrée pour minimiser la distance de contenu avec l’image de contenu et sa distance de style avec l’image de style.

En résumé, nous prendrons l’image d’entrée de base, une image de contenu que nous voulons faire correspondre, et l’image de style que nous voulons faire correspondre. Nous allons transformer l’image d’entrée de base en minimisant les distances (pertes) de contenu et de style avec la rétropropagation, créant ainsi une image qui correspond au contenu de l’image de contenu et au style de l’image de style.

Dans le processus, nous allons construire une expérience pratique et développer une intuition autour des concepts suivants :

• Exécution empressée – utiliser l’environnement de programmation impérative de TensorFlow qui évalue les opérations immédiatement
• En savoir plus sur l’exécution empressée
• Le voir en action (de nombreux tutoriels sont exécutables dans Colaboratory)
• Utilisation de l’API fonctionnelle pour définir un modèle – nous construirons un sous-ensemble de notre modèle qui nous donnera accès aux nécessaires activations intermédiaires en utilisant l’API fonctionnelle
• Exploiter les cartes de caractéristiques d’un modèle pré-entraîné – Apprenez à utiliser les modèles pré-entraînés et leurs cartes de caractéristiques
• Créer des boucles d’entraînement personnalisées – nous examinerons comment configurer un optimiseur pour minimiser une perte donnée par rapport aux paramètres d’entrée

Nous suivrons les étapes générales pour effectuer le transfert de style :

1. Visualiser les données
2. Prétraitement de base/préparation de nos données
3. Mise en place des fonctions de perte
4. Créer le modèle
5. Optimiser pour la fonction de perte

Audience : Ce post est destiné aux utilisateurs intermédiaires qui sont à l’aise avec les concepts de base de l’apprentissage automatique. Pour tirer le meilleur parti de ce post, vous devriez :

• Lire l’article de Gatys – nous expliquerons en cours de route, mais l’article fournira une compréhension plus approfondie de la tâche
• Comprendre la descente de gradient

Temps estimé : 60 min

Code:

Vous pouvez trouver le code complet de cet article à ce lien. Si vous souhaitez avancer dans cet exemple, vous pouvez trouver le colab ici.

Mise en œuvre

Nous allons commencer par activer l’exécution avide. L’exécution avide nous permet de travailler à travers cette technique de la manière la plus claire et la plus lisible.

Définir les représentations de contenu et de style

Afin d’obtenir à la fois les représentations de contenu et de style de notre image, nous allons examiner certaines couches intermédiaires dans notre modèle. Les couches intermédiaires représentent des cartes de caractéristiques qui deviennent de plus en plus ordonnées au fur et à mesure que vous descendez en profondeur. Dans ce cas, nous utilisons l’architecture de réseau VGG19, un réseau de classification d’images pré-entraîné. Ces couches intermédiaires sont nécessaires pour définir la représentation du contenu et du style de nos images. Pour une image d’entrée, nous allons essayer de faire correspondre les représentations cibles de style et de contenu correspondantes à ces couches intermédiaires.

Pourquoi des couches intermédiaires ?

Vous vous demandez peut-être pourquoi ces sorties intermédiaires au sein de notre réseau de classification d’images pré-entraîné nous permettent de définir des représentations de style et de contenu. À un haut niveau, ce phénomène peut être expliqué par le fait que pour qu’un réseau puisse effectuer une classification d’images (ce pour quoi notre réseau a été entraîné), il doit comprendre l’image. Cela implique de prendre l’image brute comme pixels d’entrée et de construire une représentation interne par le biais de transformations qui transforment les pixels de l’image brute en une compréhension complexe des caractéristiques présentes dans l’image. C’est aussi en partie la raison pour laquelle les réseaux neuronaux convolutifs sont capables de généraliser : ils sont capables de capturer les invariances et les caractéristiques définissant les classes (par exemple, chats vs chiens) qui sont agnostiques au bruit de fond et autres nuisances. Ainsi, quelque part entre l’entrée de l’image brute et la sortie de l’étiquette de classification, le modèle sert d’extracteur de caractéristiques complexes ; ainsi, en accédant aux couches intermédiaires, nous sommes capables de décrire le contenu et le style des images d’entrée.

Spécifiquement, nous allons extraire ces couches intermédiaires de notre réseau :

Modèle

Dans ce cas, nous chargeons VGG19, et alimentons notre tenseur d’entrée au modèle. Cela nous permettra d’extraire les cartes de caractéristiques (et par la suite les représentations du contenu et du style) des images de contenu, de style et générées.

Nous utilisons VGG19, comme suggéré dans l’article. De plus, comme VGG19 est un modèle relativement simple (comparé à ResNet, Inception, etc), les cartes de caractéristiques fonctionnent en fait mieux pour le transfert de style.

Pour accéder aux couches intermédiaires correspondant à nos cartes de caractéristiques de style et de contenu, nous obtenons les sorties correspondantes en utilisant l’API fonctionnelle de Keras pour définir notre modèle avec les activations de sortie souhaitées.

Avec l’API fonctionnelle, la définition d’un modèle implique simplement de définir l’entrée et la sortie : model = Model(inputs, outputs).

Dans l’extrait de code ci-dessus, nous allons charger notre réseau de classification d’images pré-entraîné. Ensuite, nous saisissons les couches d’intérêt comme nous l’avons défini précédemment. Nous définissons ensuite un modèle en définissant les entrées du modèle sur une image et les sorties sur les sorties des couches de style et de contenu. En d’autres termes, nous avons créé un modèle qui va prendre une image en entrée et sortir les couches intermédiaires de contenu et de style !

Définir et créer nos fonctions de perte (distances de contenu et de style)

Notre définition de la perte de contenu est en fait assez simple. Nous allons passer au réseau à la fois l’image de contenu désirée et notre image d’entrée de base. Cela renverra les sorties des couches intermédiaires (des couches définies ci-dessus) de notre modèle. Ensuite, nous prenons simplement la distance euclidienne entre les deux représentations intermédiaires de ces images.

Plus formellement, la perte de contenu est une fonction qui décrit la distance de contenu entre notre image d’entrée x et notre image de contenu, p . Soit Cₙₙ un réseau neuronal convolutif profond pré-entraîné. Encore une fois, dans ce cas, nous utilisons le VGG19. Soit X une image quelconque, alors Cₙₙ(x) est le réseau alimenté par X. Soit Fˡᵢⱼ(x)∈ Cₙₙ(x)et Pˡᵢⱼ(x) ∈ Cₙₙ(x) décrivent la représentation intermédiaire respective des caractéristiques du réseau avec les entrées x et p à la couche l . Ensuite, nous décrivons la distance (perte) de contenu formellement comme:

Nous effectuons la rétropropagation de manière habituelle de telle sorte que nous minimisons cette perte de contenu. Nous modifions donc l’image initiale jusqu’à ce qu’elle génère une réponse similaire dans une certaine couche (définie dans content_layer) à celle de l’image de contenu originale.

Cela peut être mis en œuvre assez simplement. Encore une fois, il prendra comme entrée les cartes de caractéristiques à une couche L dans un réseau alimenté par x, notre image d’entrée, et p, notre image de contenu, et retournera la distance de contenu.

Perte de style:

Le calcul de la perte de style est un peu plus impliqué, mais suit le même principe, cette fois en alimentant notre réseau avec l’image d’entrée de base et l’image de style. Cependant, au lieu de comparer les sorties intermédiaires brutes de l’image d’entrée de base et de l’image de style, nous comparons plutôt les matrices Gram des deux sorties.

Mathématiquement, nous décrivons la perte de style de l’image d’entrée de base, x, et de l’image de style, a, comme la distance entre la représentation de style (les matrices Gram) de ces images. Nous décrivons la représentation de style d’une image comme la corrélation entre différentes réponses de filtre données par la matrice de Gram Gˡ, où Gˡᵢⱼ est le produit interne entre la carte de caractéristiques vectorisées i et j dans la couche l. Nous pouvons voir que Gˡᵢⱼ généré sur la carte de caractéristiques pour une image donnée représente la corrélation entre les cartes de caractéristiques i et j.

Pour générer un style pour notre image d’entrée de base, nous effectuons une descente de gradient à partir de l’image de contenu pour la transformer en une image qui correspond à la représentation du style de l’image originale. Nous le faisons en minimisant la distance quadratique moyenne entre la carte de corrélation des caractéristiques de l’image de style et l’image d’entrée. La contribution de chaque couche à la perte de style totale est décrite par

où Gˡᵢⱼ et Aˡᵢⱼ sont la représentation de style respective dans la couche l de l’image d’entrée x et de l’image de style a. Nl décrit le nombre de cartes de caractéristiques, chacune de taille Ml=hauteur∗largeur. Ainsi, la perte totale de style à travers chaque couche est

où nous pondérons la contribution de la perte de chaque couche par un certain facteur wl. Dans notre cas, nous pondérons chaque couche de manière égale :

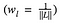
Ceci est mis en œuvre simplement :

Run Gradient Descent

Si vous n’êtes pas familier avec la descente de gradient/backpropagation ou avez besoin d’un rafraîchissement, vous devriez certainement consulter cette ressource.

Dans ce cas, nous utilisons l’optimiseur Adam afin de minimiser notre perte. Nous mettons à jour itérativement notre image de sortie de sorte qu’elle minimise notre perte : nous ne mettons pas à jour les poids associés à notre réseau, mais au lieu de cela, nous entraînons notre image d’entrée pour minimiser la perte. Pour ce faire, nous devons savoir comment nous calculons notre perte et nos gradients. Notez que l’optimiseur L-BFGS, qui est recommandé si vous êtes familier avec cet algorithme, n’est pas utilisé dans ce tutoriel car l’une des principales motivations de ce tutoriel était d’illustrer les meilleures pratiques en matière d’exécution rapide. En utilisant Adam, nous pouvons démontrer la fonctionnalité autograde/bande de gradient avec des boucles d’entraînement personnalisées.

Calculer la perte et les gradients

Nous allons définir une petite fonction d’aide qui chargera notre image de contenu et de style, les fera avancer dans notre réseau, qui sortira ensuite les représentations des caractéristiques de contenu et de style de notre modèle.

Nous utilisons ici tf.GradientTape pour calculer le gradient. Il nous permet de profiter de la différenciation automatique disponible en traçant les opérations pour calculer le gradient plus tard. Il enregistre les opérations pendant la passe avant et est ensuite capable de calculer le gradient de notre fonction de perte par rapport à notre image d’entrée pour la passe arrière.

Alors calculer les gradients est facile:

Appliquer et exécuter le processus de transfert de style

Et pour effectuer réellement le transfert de style:

Et c’est tout !

Exécutons-le sur notre image de la tortue et sur La grande vague au large de Kanagawa de Hokusai :

Voyez le processus itératif au fil du temps :

Voici d’autres exemples cool de ce que le transfert de style neuronal peut faire. Regardez !

Tentez vos propres images !

Ce que nous avons couvert:

• Nous avons construit plusieurs fonctions de perte différentes et utilisé la rétropropagation pour transformer notre image d’entrée afin de minimiser ces pertes.
• Pour ce faire, nous avons chargé un modèle pré-entraîné et utilisé ses cartes de caractéristiques apprises pour décrire la représentation du contenu et du style de nos images.
• Nos principales fonctions de perte étaient principalement le calcul de la distance en termes de ces différentes représentations.
• Nous avons implémenté cela avec un modèle personnalisé et une exécution avide.
• Nous avons construit notre modèle personnalisé avec l’API fonctionnelle.
• L’exécution avide nous permet de travailler dynamiquement avec des tenseurs, en utilisant un flux de contrôle python naturel.
• Nous avons manipulé les tenseurs directement, ce qui facilite le débogage et le travail avec les tenseurs.

Nous avons itérativement mis à jour notre image en appliquant les règles de mise à jour de nos optimiseurs en utilisant tf.gradient. L’optimiseur a minimisé les pertes données par rapport à notre image d’entrée.