Encontrar fuentes: «Norma uniforme» – noticias – periódicos – libros – scholar – JSTOR (diciembre de 2009) (Aprende cómo y cuándo eliminar este mensaje de la plantilla)
En el análisis matemático, la norma uniforme (o sup norma) asigna a las funciones acotadas de valor real o complejo f definidas sobre un conjunto S el número no negativo
‖ f ‖ ∞ = ‖ f ‖ ∞ , S = sup { | f ( x ) | : x ∈ S } . {\displaystyle |f\|_{infty }=|f\|_{infty ,S}=\sup \left{{,\left|f(x)\right|:x\in S,\right}.} 
Esta norma también se llama norma del sumo, norma de Chebyshev, norma del infinito o, cuando el sumo es de hecho el máximo, norma del máximo. El nombre de «norma uniforme» deriva del hecho de que una secuencia de funciones { f n } {{displaystyle \\_{f_{n}} 



La métrica generada por esta norma se denomina métrica de Chebyshev, en honor a Pafnuty Chebyshev, que fue el primero en estudiarla sistemáticamente.
Si permitimos funciones no acotadas, esta fórmula no produce una norma o métrica en sentido estricto, aunque la llamada métrica extendida obtenida sigue permitiendo definir una topología sobre el espacio de funciones en cuestión.
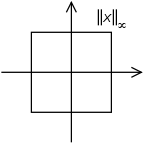
Si f es una función continua sobre un intervalo cerrado, o más generalmente un conjunto compacto, entonces está acotada y el sumo en la definición anterior se alcanza por el teorema del valor extremo de Weierstrass, por lo que podemos sustituir el sumo por el máximo. En particular, para el caso de un vector x = ( x 1 , … , x n ) {\displaystyle x=(x_{1},\dots ,x_{n})} 
‖ x ‖ ∞ = max { | x 1 | , … , | x n | } . {\displaystyle ||x\|_{\infty }=\max{{x_{1}|,\dots ,|x_{n}|}.} 
La razón del subíndice «∞» es que siempre que f es continua
lim p → ∞ ‖ f ‖ p = ‖ f ‖ ∞ , {\displaystyle \lim _{p\rightarrow \infty }||f|_{p}=\|f|_{infty },
donde
‖ f ‖ p = ( ∫ D | f | p d μ ) 1 / p {\displaystyle |f|_{p}=\left(\int _{D}left|f\right|^{p},d\mu \right)^{1/p} 
donde D es el dominio de f (y la integral equivale a una suma si D es un conjunto discreto).
La función binaria
d ( f , g ) = ‖ f – g ‖ ∞ {\displaystyle d(f,g)=||f-g|_{\infty }} 
es entonces una métrica sobre el espacio de todas las funciones acotadas (y, obviamente, cualquiera de sus subconjuntos) sobre un dominio particular. Una secuencia { fn : n = 1, 2, 3, … } converge uniformemente a una función f si y sólo si
lim n → ∞ ‖ f n – f ‖ ∞ = 0. {{displaystyle}}lim _{n}flecha derecha {{infty}}|f_{n}-f|_{infty}}=0,} lim _{n}flecha derecha {{infty}}|f_{n}-f|{infty}}=0.\Podemos definir conjuntos cerrados y cierres de conjuntos con respecto a esta topología métrica; los conjuntos cerrados en la norma uniforme se llaman a veces uniformemente cerrados y los cierres uniformes. El cierre uniforme de un conjunto de funciones A es el espacio de todas las funciones que pueden ser aproximadas por una secuencia de funciones uniformemente convergentes sobre A. Por ejemplo, una reformulación del teorema de Stone-Weierstrass es que el conjunto de todas las funciones continuas sobre {\displaystyle } 

Para funciones continuas complejas sobre un espacio compacto, esto lo convierte en un álgebra C*.