Gruppemultiplikation
Nu skal vi undersøge, hvad der sker, når vi anvender to symmetrioperationer i rækkefølge. Som et eksempel kan vi betragte molekylet \(NH_3\), som tilhører punktgruppen \(C_{3v}\). Overvej, hvad der sker, hvis vi anvender en \(C_3\\)rotation efterfulgt af en \(\sigma_v\)-reflektion. Vi skriver denne kombinerede operation \(\sigma_v\)\(C_3\) (når de skrives, opererer symmetrioperationer på det, der ligger direkte til højre for dem, ligesom operatorer gør i kvantemekanikken – vi er derfor nødt til at arbejde baglæns fra højre til venstre fra notationen for at få den korrekte rækkefølge, i hvilken operatørerne anvendes). Som vi snart skal se, er det vigtigt, i hvilken rækkefølge operationerne anvendes.
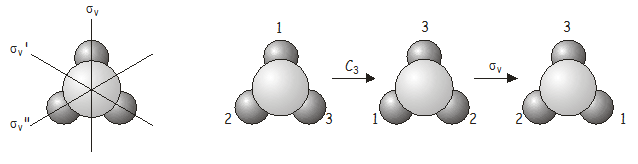
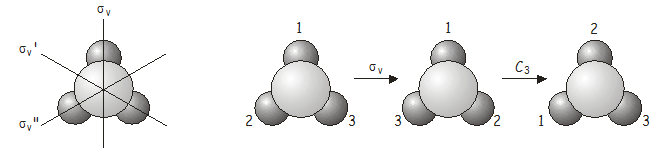
Og igen er den kombinerede operation \(C_3\)\(\sigma_v\) ækvivalent med en anden operation i punktgruppen, denne gang \(\sigma_v’\).
Der er to vigtige punkter, der illustreres af dette eksempel:
Virkningerne af at anvende to symmetrioperationer i rækkefølge inden for en given punktgruppe er sammenfattet i gruppemultiplikationstabeller. Som et eksempel er den komplette gruppemultiplikationstabel for \(C_{3v}\) ved hjælp af symmetrioperationerne som defineret i ovenstående figurer vist nedenfor. De operationer, der er skrevet langs tabellens første række, udføres først, efterfulgt af dem, der er skrevet i den første kolonne (bemærk, at tabellen ville ændre sig, hvis vi valgte at navngive \(\sigma_v\), \(\(\sigma_v’\) og \(\(\sigma_v”\) i en anden rækkefølge).