Den følgende definition af robust statistik stammer fra P. J. Hubers bog Robust Statistics.
… enhver statistisk procedure bør besidde følgende ønskelige egenskaber:
- Den bør have en rimelig god (optimal eller næsten optimal) effektivitet ved den antagne model.
- Den bør være robust i den forstand, at små afvigelser fra modelantagelserne kun i ringe grad bør forringe præstationen. …
- Visse større afvigelser fra modellen bør ikke medføre en katastrofe.
Klassisk statistik fokuserer på det første af Hubers punkter, idet den producerer metoder, der er optimale med forbehold af nogle kriterier. Dette indlæg ser på de kanoniske eksempler, der bruges til at illustrere Hubers andet og tredje punkt.
Hubers tredje punkt illustreres typisk af stikprøvens gennemsnit (gennemsnit) og stikprøvens median (middelværdi). Man kan sætte næsten halvdelen af dataene i en prøve til ∞ uden at få prøvens median til at blive uendelig. Prøvens middelværdi bliver derimod uendelig, hvis en hvilken som helst værdi i prøven er uendelig. Store afvigelser fra modellen, dvs. nogle få outliers, kan forårsage en katastrofe for stikprøvens gennemsnit, men ikke for stikprøvens median.
Det kanoniske eksempel, når man diskuterer Hubers andet punkt, går tilbage til John Tukey. Start med det enkleste lærebogseksempel på estimation: data fra en normalfordeling med ukendt middelværdi og varians 1, dvs. dataene er normal(μ, 1) med μ ukendt. Den mest effektive måde at estimere μ på er at tage stikprøvens gennemsnit, dvs. gennemsnittet af dataene.
Men antag nu, at datafordelingen ikke er præcis normal(μ, 1), men i stedet er en blanding af en standardnormalfordeling og en normalfordeling med en anden varians. Lad δ være et lille tal, f.eks. 0,01, og antag, at dataene kommer fra en normal(μ, 1)-fordeling med sandsynligheden 1-δ og dataene kommer fra en normal(μ, σ2)-fordeling med sandsynligheden δ. Denne fordeling kaldes en “kontamineret normal”, og tallet δ er mængden af kontaminering. Grunden til at bruge den kontaminerede normalmodel er, at der er tale om en ikke-normal fordeling, som kan se normal ud for øjet.
Vi kunne estimere populationens middelværdi μ ved hjælp af enten stikprøvens middelværdi eller stikprøvens median. Hvis dataene var strengt normale i stedet for en blanding, ville stikprøvens gennemsnit være den mest effektive estimator af μ. I så fald ville standardfejlen være ca. 25 % større, hvis vi brugte stikprøvemedianen. Men hvis dataene stammer fra en blanding, kan stikprøvemedianen være mere effektiv, afhængigt af størrelsen af δ og σ. Her er et plot af ARE (asymptotisk relativ effektivitet) for stikprøvemedianen sammenlignet med stikprøvens gennemsnit som en funktion af σ, når δ = 0.01.
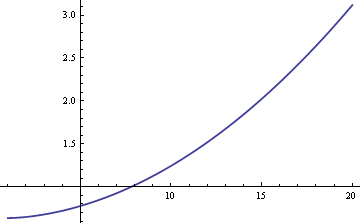
Det fremgår af plottet, at for værdier af σ større end 8 er stikprøvemedianen mere effektiv end stikprøvens middelværdi. Medianens relative overlegenhed vokser uden begrænsning, når σ stiger.
Her er et plot af ARE med σ fastsat til 10 og δ varierende mellem 0 og 1.
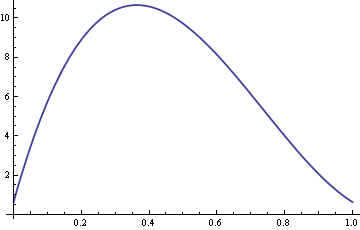
Så for værdier af δ omkring 0.4 er stikprøvemedianen over ti gange mere effektiv end stikprøvens gennemsnit.
Den generelle formel for ARE i dette eksempel er 2((1 + δ(σ2 – 1)(1 – δ + δ/σ)2)/ π.
Hvis du er sikker på, at dine data er normale uden kontaminering eller med meget lille kontaminering, er stikprøvens gennemsnit den mest effektive estimator. Men det kan være værd at risikere at opgive en smule effektivitet til gengæld for at vide, at du vil klare dig bedre med en robust model, hvis der er betydelig kontaminering. Der er større potentiale for tab ved at bruge stikprøvens gennemsnit, når der er betydelig forurening, end der er potentiel gevinst ved at bruge stikprøvens gennemsnit, når der ikke er nogen forurening.
Her er en gåde forbundet med det forurenede normaleksempel. Den mest effektive estimator for normale(μ, 1) data er stikprøvens gennemsnit. Og den mest effektive estimator for normal(μ, σ2)-data er også at tage stikprøvens gennemsnit. Hvorfor er det så ikke optimalt at tage stikprøvens gennemsnit af blandingen?
Nøglen er, at vi ikke ved, om en bestemt stikprøve kom fra normal(μ, 1)-fordelingen eller fra normal(μ, σ2)-fordelingen. Hvis vi vidste det, kunne vi adskille prøverne, foretage et gennemsnit af dem hver for sig og kombinere prøverne til et samlet gennemsnit: multiplicere det ene gennemsnit med 1-δ, multiplicere det andet med δ og lægge det sammen. Men da vi ikke ved, hvilke af blandingskomponenterne der fører til hvilke prøver, kan vi ikke vægte prøverne på passende vis. (Vi kender sandsynligvis heller ikke δ, men det er en anden sag.)
Der er andre muligheder end at bruge stikprøvens gennemsnit eller stikprøvens median. For eksempel smider den trimmede middelværdi nogle af de største og mindste værdier ud og beregner derefter gennemsnittet af alt andet. (Nogle gange fungerer sport på denne måde, idet man smider en atlets højeste og laveste karakterer fra dommerne ud). Jo flere data der smides væk i hver ende, jo mere fungerer det trimmede gennemsnit som medianen i stikprøven. Jo færre data der smides væk, jo mere virker den som stikprøvens gennemsnit.
Relateret indlæg: Effektivitet af median versus middelværdi for Student-t-fordelinger
For daglige tips om datalogi kan du følge @DataSciFact på Twitter.