Alai

Michael Fowler,UVa Physics.

Momentum har retning

Som vi diskuterede i sidste forelæsning, havde Descartes, selv før Newton formulerede sine love, med lidt hjælp fra Huygens, opdaget en dybdynamisk sandhed: i enhver kollision, eller faktisk i enhver vekselvirkning af enhver art, forblev den samlede mængde “momentum” – et mål for bevægelse – altid den samme. Impulsen for et objekt i bevægelse er defineret som produktet af massen og hastigheden, og er således en vektor: den har størrelse og retning. Hvis du står på gnidningsløse rulleskøjter og kaster en bold, bevæger du dig baglæns: du har et moment af samme størrelse som bolden, men med modsat retning, så det samlede moment (dit plus boldens) forbliver nul. Raketter fungerer på samme måde, idet de kaster materiale ud med høj hastighed. De virker ikke ved at “skubbe mod luften”, men ved at skubbe mod det materiale, de skubber ud, ligesom du skubber mod en bold, du kaster, og den skubber dig tilbage og forårsager din acceleration.

Hvis du stadig har mistanke om, at raketter virkelig skubber mod luften, så husk på, at de fungerer lige så godt i rummet! Faktisk var det en udbredt opfattelse, at når Goddard, en tidlig amerikansk raketforsker (Goddard Space Flight Center er opkaldt efter ham) talte om raketter i rummet, var han spildt sin tid. For at citere fra en leder i New York Times fra 1921: “Professor Goddard kender ikke sammenhængen mellem handling og reaktion og behovet for at have noget bedre end et vakuum at reagere imod end at have noget bedre end et vakuum at reagere imod. Han synes at mangle den grundlæggende viden, der dagligt uddeles i vores gymnasier.” Det er indlysende, at New York Times’ redaktører på daværende tidspunkt ikke havde noget imod den grundlæggende viden, der blev uddelt i dette kursus!

Som vi har diskuteret, følger bevarelsen af bevægelsesmængden i en kollision faktisk af Newtons love. Det er imidlertid et mere generelt og enklere begreb – det afhænger slet ikke af detaljerne i vekselvirkningerne osv. Denne enkelhed var åbenbart tiltalende for Einstein, som var overbevist om, at når dynamikken blev omformuleret til at omfatte de nye idéer om tid og rum, skulle bevarelsen af impuls stadig gælde i enhver inertialramme. Dette førte ham til nogle overraskende konklusioner, som vi skal se.

Momentumbevarelse på billardbordet

Som opvarmningsøvelse skal vi overveje momentumbevarelse for et sammenstød mellem to kugler på et billardbord. Vi tegner en kridtlinje ned gennem midten af poolbordet og skyder kuglerne tæt på, men på modsatte sider af kridtlinjen fra hver ende med samme hastighed, så de vil ramme hinanden i midten med et skråt slag, hvilket vil vende deres hastigheder i en lille vinkel. Med andre ord, hvis vi oprindeligt siger, at deres (lige store, modsatte retning) hastigheder var parallelle med x-retningen – kridtlinjen – så vil de efter sammenstødet også have lige store og modsatte små hastigheder i y-retningen (hastighederne i x-retningen vil være faldet meget lidt).

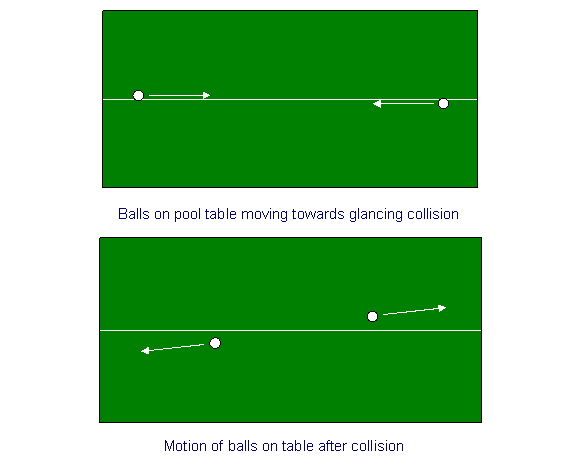
En symmetrisk rumskibssammenstød

Nu skal vi gentage øvelsen i stor skala. Lad os antage, at vi et eller andet sted i rummet, langt fra alle gravitationsfelter, udlægger en snor, der er en million kilometer lang. (Den kunne være mellem vores to ure i tidsudvidelseseksperimentet). Denne streng svarer til kridtstregen på billardbordet. Lad os nu antage, at vi har to identiske rumskibe, der nærmer sig hinanden med lige store og modsatte hastigheder parallelt med snoren fra snorens to ender, og som er rettet således, at de kommer ud for en let glidende kollision, når de mødes i midten. Det fremgår af situationens symmetri, at impulsen er bevaret i begge retninger. Især er den hastighed, hvormed det ene rumskib bevæger sig væk fra snoren efter kollisionen – dets y-hastighed – lige så stor som den hastighed, hvormed det andet rumskib bevæger sig væk fra snoren.

Men betragt nu denne kollision som observeret af en person i et af rumskibene, kald det A. Før kollisionen ser han, at snoren bevæger sig meget hurtigt ved vinduet, f.eks. et par meter væk. Efter kollisionen ser han, at strengen bevæger sig væk med, lad os sige, 15 meter i sekundet. Det skyldes, at rumskib A har optaget en hastighed vinkelret på snoren på 15 meter i sekundet. Da der er tale om en fuldstændig symmetrisk situation, ville en observatør på rumskib B i mellemtiden helt sikkert udlede, at hendes rumskib også bevægede sig væk fra snoren med 15 meter i sekundet.

Hvor symmetrisk er det egentlig?

Det afgørende spørgsmål er: Hvor hurtigt ser en observatør i rumskib A, at rumskib B bevæger sig væk fra snoren? Lad os antage, at rumskib B i forhold til rumskib A bevæger sig væk (i x-retningen) med 0,6c. Først skal vi huske på, at afstande vinkelret på bevægelsesretningen ikke er Lorentz-kontraherede. Når observatøren i rumskib B siger, at hun har bevæget sig 15 meter længere væk fra snoren i et sekundsinterval, vil observatøren, der ser denne bevægelse fra rumskib A, derfor være enig i de 15 meter – men uenig i det ene sekund! Han vil sige, at hendes ure går langsomt, så målt af hans ure er der gået 1,25 sekunder, mens hun bevæger sig 15 meter i y-retningen.

Det følger heraf, at som følge af tidsudvidelse forårsager dette sammenstød set fra rumskib A ikke lige store og modsatte hastigheder for de to rumskibe i y-retningen. Oprindeligt bevægede begge rumskibe sigparallelt til x-aksen, der var zeromomentum i y-retningen. Hvordan kan vi så hævde, at der er nul samlet momentum i y-retningen efter kollisionen, når de identiske rumskibe ikke har samme og modsatrettede hastigheder?

Einstein redder momentumbevarelsen

Einstein var så sikker på, at momentumbevarelsen altid må holde, at han reddede den med en dristig hypotese: Et objekts masse må afhænge af dets hastighed! Faktisk må massen stige med hastigheden på en sådan måde, at den ophæver den lavere y-retningshastighed som følge af tidsudvidelse. Det vil sige, at hvis et objekt i hvile har en masse m og bevæger sig med en hastighed v, vil det have en inerti svarende til en “relativistisk masse” m rel =m/ 1-( v 2 / c 2 ) .Så bliver impulsen

p → = m rel v → =m v → / 1-( v 2 / c 2 ) .

Bemærk, at denne relativistiske masseforøgelse er en umærkeligt lille effekt ved almindelige hastigheder, men når et objekt nærmer sig flyvehastigheden, stiger massen ubegrænset!

Massen stiger virkelig med hastigheden

Det virker som en høj pris at betale for at redde momentumbevarelsen, hvis man beslutter, at objekters masse skal afhænge af hastigheden på denne måde! Det er imidlertid en forudsigelse, som ikke er vanskelig at kontrollere ved hjælp af eksperimenter. Den første bekræftelse kom i 1908, da man afbøjede hurtige elektroner i et vakuumrør. Faktisk har elektronerne i et gammeldags farvefjernsynsrør ca. en halv procent mere inerti end elektroner i hvile, og det skal der tages højde for ved beregningen af de magnetfelter, der bruges til at lede dem til skærmen.

Meget mere dramatisk er det, at man i moderne partikelacceleratorer anvender meget kraftige elektriske felter til at accelerere elektroner, protoner og andre partikler. I praksis viser det sig, at disse partikler har brug for større og større kræfter til yderligere acceleration, efterhånden som man nærmer sig lysets hastighed. Derfor er lysets hastighed en naturlig absolut hastighedsgrænse. Partikler accelereres til hastigheder, hvor deres relativistiske masse er tusindvis af gange større end deres masse målt i hvile, som normalt kaldes “hvilemassen”.

…Eller gør den?

Der er faktisk fortsat debat blandt fysikere om dette begreb om relativistisk masse. Debatten er i høj grad semantisk: ingen er i tvivl om, at det korrekte udtryk for impulsen for en partikel med hvilemassen m, der bevæger sig med hastigheden v → , er p → = m 1- v 2 / c 2 v → . Men især partikelfysikere, hvoraf mange bruger deres liv på at måle partiklers hvilemasse med stor præcision, er ikke begejstrede for at skrive dette som p → = m rel v → . De bryder sig ikke om tanken om en variabel masse. For det første kan det give indtryk af, at en partikel vokser i størrelse, når den accelererer, eller at dens indre struktur i det mindste ændres på en eller anden måde. I virkeligheden undergår en relativistisk partikel blot en Lorentz-kontraktion langs bevægelsesretningen, ligesom alt andet. Den går fra en kugleform til en skiveform med samme tværgående radius.

Hvordan kan man så forstå denne “masseforøgelse”? Som sædvanlig havde Einstein ret: han bemærkede, at enhver form for energi har inerti. Selve den kinetiske energi har inerti. Nu er “inerti” en definerende egenskab ved masse. Den anden grundlæggende egenskab ved masse er, at den har en gravitationel tiltrækningskraft. Gør denne kinetiske energi det? For at se svaret kan man betragte en kugle fyldt med gas. Den vil skabe et sfærisk symmetrisk gravitationsfelt uden for sig selv med en styrke, der er proportional med den samlede masse. Hvis vi nu opvarmer gassen, vil gaspartiklerne have denne øgede (relativistiske) masse, svarende til deres øgede kinetiske energi, og det ydre gravitationsfelt vil være øget proportionalt. (Ingen er i tvivl om begge dele.)

Så den “relativistiske masse” har faktisk de to grundlæggende egenskaber ved masse: inerti og gravitationstiltrækning. (Som det vil fremgå af de følgende forelæsninger, er denne relativistiske masse intet andet end den samlede energi, idet selve hvilemassen nu betragtes som energi.)

På et mere trivielt plan er nogle lærere imod at indføre den relativistiske masse, fordi de frygter, at eleverne vil antage, at den kinetiske energi for en partikel i relativistisk bevægelse blot er 1 2 m v → 2 ved hjælp af den relativistiske masse – det er den ikke, som vi skal se om lidt.

Fodnote: For alle, der måske på et tidspunkt vil gå videre til en matematisk sofistikeret behandling, skal det tilføjes, at hvilemassen spiller en vigtig rolle som en invariant, når man går fra en referenceramme til en anden, men den “relativistiske masse”, der bruges her, er i virkeligheden bare den første komponent (energien) af den firedimensionale energi-momentumvektor for en partikel, og er derfor ikke en invariant.

Kinetisk energi og masse for meget hurtige partikler

Lad os tænke på den kinetiske energi af en af dissepartikler, der bevæger sig tæt på lysets hastighed. Husk på, at vi i en tidligere forelæsning fandt, at den kinetiske energi for en almindelig ikke-relativistisk (dvs. langsomt bevægende) masse m var 1 2 m v 2 . Den måde, vi gjorde det på, var ved at overveje, hvor meget arbejde vi skulle udføre for at løfte den op i en bestemt højde: vi skulle udøve en kraft svarende til dens vægt W for at løfte den op i højden h, idet det samlede arbejde, eller den udførte energi, var kraft x afstand, Wh. Da den faldt ned igen, udførte tyngdekraften W nøjagtig det samme arbejde Wh på den faldende genstand, men denne gang gik arbejdet til at accelerere genstanden, så den fik kinetisk energi. Da vi ved, hvor hurtigt faldende genstande opsamler fart, kunne vi konkludere, at den kinetiske energi var 1 2 m v 2 . (For nærmere oplysninger henvises til den foregående forelæsning.)

Mere generelt kunne vi have accelereret massen med en vilkårligkonstant kraft F og fundet det arbejde, som kraften udførte (kraft x afstand) for at få den til at nå hastigheden v fra en stående start. Massens kinetiske energi, E= 1 2 m v 2 , er nøjagtig lig med det arbejde, som kraften udførte for at bringe massen op til denne hastighed. (Det kan på tilsvarende måde vises, at hvis en kraft påføres en partikel, der allerede bevæger sig med hastigheden u, og den accelereres til hastigheden v, er det nødvendige arbejde 1 2 m v 2 – 1 2 m u 2 . )

Det er interessant at forsøge at gentage øvelsen for en partikel, der bevæger sig meget tæt på lysets hastighed, som partiklerne i de acceleratorer, der er nævnt i det foregående afsnit. Newtons anden lov, i formen

Kraft = impulsændringshastighed

er stadig sand, men tæt på lysets hastighed ændrer hastigheden sig ubetydeligt, mens kraften fortsætter med at virke – i stedet øges massen! Derfor kan vi med en god tilnærmelse skrive:

Kraft = (masseændringshastighed) x c

hvor c som sædvanlig er lysets hastighed. For at blive mere specifik, antager vi, at vi har en konstant kraft F, der skubber en partikel. På et tidspunkt har partiklen masse M og en hastighed ekstremt tæt på c. Et sekund senere vil partiklen, da kraften fortsætter med at arbejde på partiklen og dermed øge dens bevægelsesmængde i henhold til Newtons anden lov, have masse M+m, hvor m er masseforøgelsen som følge af det arbejde, som kraften udfører.

Hvad er stigningen i partiklens kinetiske energi E i løbet af denne periode på et sekund? I nøjagtig analogi med det ikke-relativistiske tilfælde, der er gennemgået ovenfor, er det blot det arbejde, der udføres af kraften i denne periode. Da partiklens masse ændres med m i løbet af et sekund, er m også den hastighed hvormed massen ændres. Derfor kan vi ud fra Newtons anden lov i formen

Kraft = (masseændringshastighed) x c,

skrive

Kraft =mc.

Stigningen i den kinetiske energi E i løbet af et sekund er blot det arbejde, som kraften udfører,

E= kraft x afstand.

Da partiklen bevæger sig stort set med flyvehastighed, er den afstand, som kraften virker i løbet af et sekund, blot c meter, c=3× 10 8 .

Så det samlede arbejde, som kraften udfører i det pågældende sekund, er kraft x afstand =mc×c=m c 2 .

Dermed er forholdet mellem stigningen i masse af den relativistiske partikel og dens stigning i kinetisk energi:

E=m c 2 .

Kinetisk energi og masse for langsomme partikler

Husk, at for at få Newtons love til at være sande i alle inertialsystemer, måtte vi antage en stigning i massen med hastigheden med faktoren 1/ 1-( v 2 / c 2 ) . Dette indebærer, at selv en genstand, der bevæger sig langsomt, har en lille stigning i sin masse, når den bevæger sig!

Hvordan hænger denne lille stigning sammen med den kinetiske energi? Betragt en masse M, der bevæger sig med en hastighed v, der er meget mindre end lysets hastighed. Dens kinetiske energi E= 1 2 M v 2 , som diskuteret ovenfor. Dens masse er M/ 1-( v 2 / c 2 ) , som vi kan skrive som M+m. Hvad er m?

Da vi taler om hastigheder, som vi kender, som f.eks. et jetfly, hvor v/c, er meget lille, kan vi bruge nogle enkle matematiske tricks for at gøre tingene lettere.

Den første er en god tilnærmelse for kvadratroden af 1-x, når x er meget mindre end et:

1-x ≅1- 1 2 x for x≪1.

Du kan nemt kontrollere dette med din lommeregner: prøv x= 1 100 , du finder 99 100 =0,994987 … hvilket er ekstremt tæt på 1- 1 2 1 100 =0,995 !

Den næste tilnærmelse er

1 1-x ≅1+x for x≪1.

Dette er også let at kontrollere: Tag igen x= 1 100 : 1 1 1-x = 1 99 100 = 100 99 100 = 100 99 =1,01010… ,og 1+x= 101 100 =1,01.

Ved anvendelse af disse tilnærmelser med x=v/c kan vi tilnærme 1-( v 2 / c 2 ) som 1- 1 2 ( v 2 / c 2 ) ,og derefter 1/( 1- 1 2 ( v 2 / c 2 ) ) som 1+ 1 2 ( v 2 / c 2 ) .

Det betyder, at den samlede masse ved hastigheden v

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ),

og ved at skrive dette som M+m, kan vi se, at masseforøgelsen m er lig med 1 2 M v 2 / c 2 .

Det betyder, at – igen – masseforøgelsen m er relateret til den kinetiske energi E ved E=m c 2 .

Det er faktisk ikke svært at vise med lidt regning, at over hele hastighedsområdet fra nul til så tæt på lysets hastighed som man vil, oplever en partikel i bevægelse en masseforøgelse, der er relateret til dens kinetiske energi med E=m c 2 . For at forstå, hvorfor dette ikke bemærkes i hverdagen, kan man prøve et eksempel, f.eks. et jetfly på 100 tons, der bevæger sig med en hastighed på 2.000 km/t. 100 tons er 100.000 kg, 2.000 mph er ca. 1.000 meter i sekundet. Det er en kinetisk energi 1 2 M v 2 på ½ ×1011 Joule, men den tilsvarende masseændring af flyet ned med faktoren c 2 , 9× 10 16 , hvilket giver en faktisk masseforøgelse på ca. et halvt milligram, hvilket ikke er så let at opdage!

E = mc2

Vi har set ovenfor, at når en kraft udfører et arbejde, der accelererer et legeme for at give det kinetisk energi, øges legemets masse med et beløb svarende til det samlede arbejde, der udføres af kraften, den overførte energi E, divideret med c 2 . Hvad med, når en kraft udøver et arbejde på et legeme, som ikke fremskynder det, så der ikke sker nogen forøgelse af den kinetiske energi? Hvad nu, hvis jeg f.eks. bare løfter noget med en jævn hastighed, hvorved det får potentiel energi? Det viser sig, at der også i dette tilfælde er en masseforøgelse, der er givet ved E=m c 2 , som naturligvis er ufattelig lille for hverdagsobjekter.

Det er imidlertid en målbar og vigtig effekt inden for kernefysikken. For eksempel har heliumatomet en kerne, som har to protoner og to neutroner, der er bundet meget tæt sammen af en stærk kernetiltrækningskraft. Hvis den ydre kraft er tilstrækkelig stor, kan denne kerne adskilles i to “tunge brintkerner”, som hver har én proton og én neutron. Der skal bruges meget energi udefra for at opnå denne adskillelse, og det viser sig, at den samlede masse af de to tunge brintkerner er målbart tungere (ca. en halv procent) end den oprindelige heliumkerne. Denne ekstra masse, ganget med c 2 , er lige så stor som den energi, der er nødvendig for at splitte heliumkernen i to. Endnu vigtigere er det, at denne energi kan genvindes ved at lade de to tunge brintkerner kollidere og slutte sig sammen for at danne en heliumkerne igen. (De er begge elektrisk positivt ladede, så de frastøder hinanden, og de skal mødes ret hurtigt for at overvinde denne frastødning og komme så tæt på hinanden, at den meget stærkere kernetiltrækning slår igennem). Dette er den grundlæggende energikilde i brintbomben og i solen.

Det viser sig, at alle former for energi, både kinetisk energi og forskellige former for potentiel energi, har en masse, der er givet ved E=m c 2 . For kernereaktioner er masseændringen typisk af størrelsesordenen en tusindedel af den samlede masse, og den kan let måles. For kemiske reaktioner er ændringen af størrelsesordenen en milliarddel af den samlede masse og kan i øjeblikket ikke måles.

forrige indeks