Ryhmien kertolasku
Jatkossa tutkimme, mitä tapahtuu, kun sovellamme kahta symmetriaoperaatiota peräkkäin. Tarkastellaan esimerkkinä \(NH_3\)-molekyyliä, joka kuuluu \(C_{3v}\)-pisteryhmään. Tarkastellaan, mitä tapahtuu, jos sovelletaan \(C_3\)-rotaatiota ja sen jälkeen \(\sigma_v\)-heijastusta. Kirjoitetaan tämä yhdistetty operaatio \(\sigma_v\)\(C_3\) (kirjoitettuna symmetriaoperaatiot vaikuttavat suoraan niiden oikealla puolella olevaan asiaan, aivan kuten operaattorit kvanttimekaniikassa – meidän on siis työskenneltävä oikealta vasemmalle, jotta saamme operaattoreiden oikean järjestyksen). Kuten tulemme pian näkemään, operaatioiden soveltamisjärjestys on tärkeä.
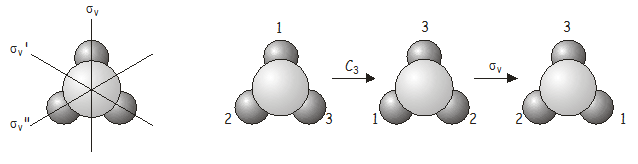
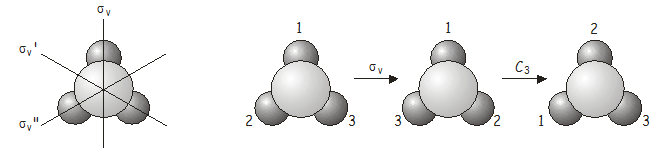
Jälleen, yhdistetty operaatio \(C_3\)\(\sigma_v\) on ekvivalenttinen toiselle pistemäisen ryhmän operaatiolle, tällä kertaa \(\sigma_v’\).
Tämä esimerkki havainnollistaa kahta tärkeää seikkaa:
Kahden symmetriaoperaation peräkkäisen soveltamisen vaikutukset tietyssä pisteryhmässä on tiivistetty ryhmäkerrointaulukoihin. Esimerkkinä alla on esitetty täydellinen ryhmäkerrointaulukko \(C_{3v}\):lle käyttäen yllä olevissa kuvissa määriteltyjä symmetriaoperaatioita. Taulukon ensimmäiselle riville kirjoitetut operaatiot suoritetaan ensin ja sen jälkeen ensimmäiseen sarakkeeseen kirjoitetut operaatiot (huomaa, että taulukko muuttuisi, jos haluaisimme nimetä \(\sigma_v\), \(\sigma_v’\) ja \(\sigma_v”\) jossakin muussa järjestyksessä).