Seuraava robustin tilastojen määritelmä on peräisin P. J. Huberin kirjasta Robust Statistics.
… millä tahansa tilastollisella menettelyllä tulisi olla seuraavat toivottavat ominaisuudet:
- Sen tulisi olla kohtuullisen hyvä (optimaalinen tai lähes optimaalinen) tehokkuus oletetulla mallilla.
- Sen tulisi olla robusti siinä mielessä, että pienet poikkeamat mallioletuksista heikentävät suorituskykyä vain vähän. …
- Hieman suurempien poikkeamien mallista ei pitäisi aiheuttaa katastrofia.
Klassinen tilastotiede keskittyy ensimmäiseen Huberin kohdista ja tuottaa menetelmiä, jotka ovat optimaalisia tietyin kriteerein. Tässä postauksessa tarkastellaan kanonisia esimerkkejä, joita käytetään havainnollistamaan Huberin toista ja kolmatta kohtaa.
Huberin kolmatta kohtaa havainnollistetaan tyypillisesti otoksen keskiarvolla (keskiarvo) ja otoksen mediaanilla (keskiarvo). Lähes puolet otoksen tiedoista voidaan asettaa arvoon ∞ ilman, että otoksen mediaani muuttuu äärettömäksi. Otoskeskiarvosta sen sijaan tulee ääretön, jos mikä tahansa otoksen arvo on ääretön. Suuret poikkeamat mallista, eli muutamat poikkeamat, voivat aiheuttaa katastrofin otoskeskiarvolle, mutta eivät otoksen mediaanille.
Kanoninen esimerkki Huberin toista kohtaa käsiteltäessä juontaa juurensa John Tukeyyn. Lähdetään liikkeelle yksinkertaisimmasta oppikirjaesimerkistä estimoinnista: data normaalijakaumasta, jonka keskiarvo on tuntematon ja varianssi 1, eli data on normal(μ, 1), jossa μ on tuntematon. Tehokkain tapa estimoida μ on ottaa otoskeskiarvo, datan keskiarvo.
Mutta oletetaan nyt, että datan jakauma ei ole täsmälleen normaali(μ, 1), vaan se on sekoitus vakionormaalijakaumasta ja normaalijakaumasta, jolla on eri varianssi. Olkoon δ pieni luku, vaikkapa 0,01, ja oletetaan, että data on peräisin normaalijakaumasta(μ, 1) todennäköisyydellä 1-δ ja data on peräisin normaalijakaumasta(μ, σ2) todennäköisyydellä δ. Tätä jakaumaa kutsutaan ”kontaminoituneeksi normaaliksi” ja luku δ on kontaminaation määrä. Syy kontaminoituneen normaalin mallin käyttämiseen on se, että kyseessä on epänormaali jakauma, joka saattaa näyttää silmin nähden normaalilta.
Voisimme arvioida populaation keskiarvon μ joko otoskeskiarvon tai otoksen mediaanin avulla. Jos aineisto olisi tiukasti normaali eikä sekoitus, otoskeskiarvo olisi tehokkain estimaattori μ:lle. Tällöin keskivirhe olisi noin 25 % suurempi, jos käyttäisimme otoksen mediaania. Mutta jos aineisto on peräisin sekoituksesta, otosmediaani voi olla tehokkaampi, riippuen δ:n ja σ:n koosta. Tässä on kuvaaja otosmediaanin ARE:stä (asymptoottinen suhteellinen tehokkuus) verrattuna otoskeskiarvoon σ:n funktiona, kun δ = 0.01.
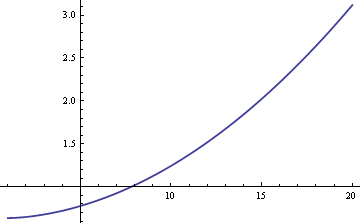
Kuvio osoittaa, että σ:n arvoilla, jotka ovat suurempia kuin 8, otoksen mediaani on tehokkaampi kuin otoksen keskiarvo. Mediaanin suhteellinen paremmuus kasvaa rajattomasti σ:n kasvaessa.
Tässä on ARE:n kuvaaja, kun σ on kiinnitetty 10:een ja δ vaihtelee 0:n ja 1:n välillä.
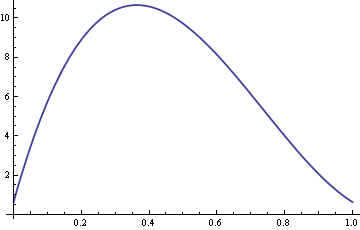
Siinä tapauksessa, kun δ:n arvot ovat noin 0.4, otosmediaani on yli kymmenen kertaa tehokkaampi kuin otoskeskiarvo.
Yleinen kaava ARE:lle tässä esimerkissä on 2((1 + δ(σ2 – 1)(1 – δ + δ/σ)2)/ π.
Jos olet varma siitä, että aineistosi on normaali ja että siinä ei ole kontaminaatiota lainkaan tai on hyvin vähän kontaminaatiota, otoskeskiarvo on tehokkain estimaattori. Mutta voi olla kannattavaa ottaa riski luopua hieman tehokkuudesta vastineeksi siitä, että tiedät pärjääväsi paremmin robustilla mallilla, jos kontaminaatio on merkittävää. Otoskeskiarvon käyttämisessä on enemmän potentiaalista tappiota, kun on merkittävää kontaminaatiota, kuin potentiaalista hyötyä otoskeskiarvon käyttämisessä, kun ei ole kontaminaatiota.
Tässä on kontaminoituneen normaalin esimerkkiin liittyvä pulma. Tehokkain estimaattori normaalille(μ, 1) aineistolle on otoskeskiarvo. Ja tehokkain estimaattori normal(μ, σ2)-aineistolle on myös otoskeskiarvo. Miksi sitten ei ole optimaalista ottaa seoksen otoskeskiarvoa?
Keskeistä on se, että emme tiedä, onko tietty näyte tullut normaalijakaumasta(μ, 1) vai normaalijakaumasta(μ, σ2). Jos tietäisimme, voisimme erottaa näytteet toisistaan, keskiarvoistaa ne erikseen ja yhdistää näytteet kokonaiskeskiarvoksi: kertomalla yhden keskiarvon 1-δ:llä, kertomalla toisen δ:llä ja laskemalla yhteen. Mutta koska emme tiedä, mitkä seoskomponentit johtavat mihinkin näytteisiin, emme voi punnita näytteitä asianmukaisesti. (Emme luultavasti tiedä myöskään δ:tä, mutta se on eri asia.)
On muitakin vaihtoehtoja kuin käyttää otoskeskiarvoa tai otoskeskiarvoa. Esimerkiksi trimmattu keskiarvo heittää pois joitakin suurimpia ja pienimpiä arvoja ja keskiarvoistaa sitten kaiken muun. (Joskus urheilussa toimitaan näin, jolloin heitetään pois urheilijan suurimmat ja pienimmät arvosanat tuomareilta). Mitä enemmän tietoja heitetään pois kummastakin päästä, sitä enemmän typistetty keskiarvo toimii otoksen mediaanin tavoin. Mitä vähemmän dataa heitetään pois, sitä enemmän se käyttäytyy kuin otoskeskiarvo.
Related post: Mediaanin ja keskiarvon tehokkuus Student-t-jakaumille
Tietotiedettä koskevia päivittäisiä vinkkejä saat seuraamalla @DataSciFactia Twitterissä.