Alai

By Raymond Yuan, Software Engineering Intern

Tässä opetusohjelmassa opettelemme käyttämään syväoppimista kuvien sommitteluun toisen kuvan tyyliin (oletko koskaan toivonut voivasi maalata kuin Picasso tai Van Gogh?). Tämä tunnetaan nimellä neuraalinen tyylinsiirto! Tämä tekniikka esitellään Leon A. Gatysin artikkelissa A Neural Algorithm of Artistic Style, joka on loistavaa luettavaa, ja sinun kannattaa ehdottomasti tutustua siihen.

Neuraalinen tyylinsiirto on optimointitekniikka, jota käytetään ottamaan kolme kuvaa, sisältökuva, tyylin referenssikuva (kuten kuuluisan taidemaalarin taideteos) ja sisääntuleva kuva, jonka haluat tyylitellä – ja sekoittamaan ne yhteen siten, että sisääntuleva kuva muunnetaan näyttämään sisältökuvan kaltaiselta, mutta se on kuitenkin ”maalattava” tyylikuvan tyyliin.

Otetaan esimerkiksi kuva tästä kilpikonnasta ja Katsushika Hokusain teos Suuri aalto Kanagawan edustalla:

Miltä nyt näyttäisi, jos Hokusai päättäisi lisätä kilpikonnan kuvaan aaltojensa tekstuuria tai tyyliä? Jotain tällaista?

Onko tämä taikuutta vai pelkkää syväoppimista? Onneksi tässä ei ole kyse mistään taikuudesta: tyylinsiirto on hauska ja mielenkiintoinen tekniikka, joka esittelee neuroverkkojen kykyjä ja sisäisiä representaatioita.

Neuraalisen tyylinsiirron periaatteena on määritellä kaksi etäisyysfunktiota, joista toinen kuvaa sitä, kuinka erilainen kahden kuvan sisältö on, Lsisältö, ja toinen kuvaa näiden kahden kuvan eroa tyylin suhteen, Lstyle. Sitten, kun annetaan kolme kuvaa, haluttu tyylikuva, haluttu sisältökuva ja syöttökuva (alustetaan sisältökuvalla), yritämme muuntaa syöttökuvan siten, että minimoimme sisältöetäisyyden sisältökuvaan ja sen tyylietäisyyden tyylikuvaan.

Yhteenvetona, otamme lähtökohdaksi syöttökuvan, sisältökuvan, jota haluamme sovittaa, ja tyylikuvan, jota haluamme sovittaa. Muunnamme perustulokuvan minimoimalla sisällön ja tyylin etäisyydet (häviöt) backpropagationin avulla, jolloin luomme kuvan, joka vastaa sisällön kuvan sisältöä ja tyylin kuvan tyyliä.

Prosessin aikana hankimme käytännön kokemusta ja kehitämme intuitiota seuraavista käsitteistä:

• Eager Execution – käytämme TensorFlow’n imperatiivista ohjelmointiympäristöä, joka arvioi operaatiot välittömästi
• Oppiaksemme lisää eager executionista
• Näemme sen toiminnassa (monet opetusohjelmat ovat ajettavissa Colaboratoriossa)
• Functional API:n käyttäminen mallin määrittelyyn – rakennamme osamallimme osajoukon, joka antaa meille pääsyn tarpeellisiin väliaktivoinnit Functional API:n avulla
• Esivalmennetun mallin ominaisuuskarttojen hyödyntäminen – opettelemme käyttämään esivalmennettuja malleja ja niiden ominaisuuskarttoja
• Mukautettujen harjoittelusilmukoiden luominen – tarkastelemme, miten optimoija asetetaan minimoimaan tietty häviö tuloparametrien suhteen

Seurataan yleisiä vaiheita tyylinsiirron suorittamiseksi:

1. Visualize data
2. Basic Preprocessing/preparing our data
3. Set up loss functions
4. Create model
5. Optimize for loss function

Audience: Tämä viesti on suunnattu keskitason käyttäjille, jotka hallitsevat koneoppimisen peruskäsitteet. Saadaksesi kaiken irti tästä postauksesta, sinun tulisi:

• Lukea Gatysin artikkeli – selitämme matkan varrella, mutta artikkeli antaa perusteellisemman ymmärryksen tehtävästä
• Ymmärtää gradienttilaskeutuminen

Aika Arvioitu: 60 min

Koodi:

Tämän artikkelin koko koodi löytyy tästä linkistä. Jos haluat käydä tämän esimerkin vaiheittain läpi, löydät colabin täältä.

Toteutus

Aloitamme ottamalla käyttöön innokkaan suorituksen. Lindgren Wikimedia Commonsista ja Image of The Great Wave Off Kanagawa from by Katsushika Hokusai Public Domain

Sisällön ja tyylin esitystapojen määrittely

Kuvamme sekä sisällön että tyylin esitystapojen saamiseksi tarkastelemme joitain välitasoja mallissamme. Välikerrokset edustavat ominaisuustietokarttoja, jotka muuttuvat yhä korkeammalle järjestetyiksi syvemmälle mentäessä. Tässä tapauksessa käytämme verkkoarkkitehtuuria VGG19, joka on esivalmennettu kuvanluokitusverkko. Nämä välikerrokset ovat tarpeen sisällön ja tyylin esittämisen määrittelemiseksi kuvistamme. Syöttökuvalle yritämme löytää vastaavat tyylin ja sisällön tavoitedespressiot näissä välikerroksissa.

Miksi välikerrokset?

Voit ehkä ihmetellä, miksi nämä esiharjoittelemamme kuvanluokitusverkon välituotokset mahdollistavat tyylin ja sisällön representaatioiden määrittelyn. Korkealla tasolla tämä ilmiö voidaan selittää sillä, että jotta verkko voi suorittaa kuvanluokittelua (johon verkkomme on koulutettu), sen on ymmärrettävä kuva. Tämä edellyttää, että raakakuva otetaan syöttöpikseleiksi ja rakennetaan sisäinen esitys muunnosten avulla, jotka muuttavat raakakuvan pikselit monimutkaiseksi ymmärrykseksi kuvassa esiintyvistä piirteistä. Tämä on myös osittain syy siihen, miksi konvoluutiohermoverkot pystyvät yleistämään hyvin: ne pystyvät vangitsemaan luokkien (esim. kissat vs. koirat) sisällä olevat invarianssit ja määrittelevät piirteet, jotka ovat riippumattomia taustakohinasta ja muista häiriötekijöistä. Näin ollen jossain välissä, jossa raakakuva syötetään ja luokitusmerkki tulostetaan, malli toimii monimutkaisena ominaisuuksien poimijana; näin ollen käyttämällä välikerroksia pystymme kuvaamaan syötettyjen kuvien sisältöä ja tyyliä.

Kohtaisesti vedämme nämä välikerrokset verkostostamme:

Malli

Tässä tapauksessa lataamme VGG19:n ja syötämme syöttöksemme tensorimme malliin. Näin voimme poimia sisällön, tyylin ja tuotettujen kuvien ominaisuuskartat (ja sen jälkeen sisällön ja tyylin representaatiot).

Käytämme VGG19:ää, kuten paperissa ehdotetaan. Lisäksi, koska VGG19 on suhteellisen yksinkertainen malli (verrattuna ResNetiin, Inceptioniin jne.), ominaisuuskartat toimivat itse asiassa paremmin tyylinsiirrossa.

Käyttääksemme tyyli- ja sisältöominaisuuskarttojamme vastaavia välikerroksia, saamme vastaavat ulostulot käyttämällä Keras Functional API:ta määrittelemällä mallimme halutuilla ulostulon aktivoinneilla.

Funktionaalisen API:n avulla mallin määrittelemiseen kuuluu yksinkertaisesti sisääntulon ja ulostulon määrittäminen: model = Model(inputs, outputs).

Yllä olevassa koodinpätkässä lataamme esivalmennetun kuvanluokitusverkkomme. Sitten nappaamme aiemmin määrittelemämme kiinnostavat kerrokset. Sitten määrittelemme mallin asettamalla mallin syötteeksi kuvan ja tuotoksiksi tyyli- ja sisältökerrosten tuotokset. Toisin sanoen loimme mallin, joka ottaa syötekuvan ja antaa tulosteet sisällön ja tyylin välikerroksille!

Määritellään ja luodaan häviöfunktiomme (sisällön ja tyylin etäisyydet)

Sisällön häviömäärittelymme on itse asiassa melko yksinkertainen. Annamme verkolle sekä halutun sisältökuvan että perustulokuvamme. Tämä palauttaa mallimme välikerrosten tuotokset (edellä määritellyistä kerroksista). Sitten otamme yksinkertaisesti euklidisen etäisyyden näiden kuvien kahden välimuotoisen esityksen väliltä.

Muodollisemmin sisältöhäviö on funktio, joka kuvaa sisällön etäisyyttä tulokuvastamme x ja sisältökuvastamme p . Olkoon Cₙₙ valmiiksi koulutettu syvä konvoluutiohermoverkko. Tässäkin tapauksessa käytämme VGG19:ää. Olkoon X mikä tahansa kuva, niin Cₙₙ(x) on verkko, jota syötetään X:llä. Olkoon Fˡᵢⱼ(x)∈ Cₙₙ(x)ja Pˡᵢⱼ(x) ∈ Cₙₙ(x) kuvaavat verkon vastaavaa ominaisuuksien välimuoto-edustusta, jolla on syötteet x ja p kerroksessa l . Tällöin kuvaamme sisällön etäisyyden (tappion) muodollisesti seuraavasti:

Suoritamme backpropagationin tavalliseen tapaan siten, että minimoimme tämän sisällön tappion. Muutamme siis alkuperäistä kuvaa, kunnes se tuottaa tietyssä kerroksessa (määritelty kohdassa content_layer) samanlaisen vasteen kuin alkuperäinen sisältökuva.

Tämä voidaan toteuttaa melko yksinkertaisesti. Jälleen se ottaa syötteenä piirrekartat kerroksessa L verkossa, jota syötetään x:llä, syöttökuvallamme, ja p:llä, sisältökuvallamme, ja palauttaa sisällön etäisyyden.

Tyylihäviö:

Tyylihäviön laskeminen on hiukan mutkikkaampaa, mutta se noudattaa samaa periaatetta, tällä kertaa syöttämällä verkkoomme lähtökohtainen syöttökuva ja tyylikuva. Sen sijaan, että vertaisimme perustulokuvan ja tyylikuvan raakoja välituloksia, vertaamme kuitenkin näiden kahden tuloksen Gram-matriiseja.

Matemaattisesti kuvaamme perustulokuvan x ja tyylikuvan a tyylihäviötä näiden kuvien tyylirepresentaatioiden (Gram-matriisien) välisenä etäisyytenä. Kuvaamme kuvan tyyliedustusta eri suodatinvasteiden välisenä korrelaationa, jonka antaa Gram-matriisi Gˡ, jossa Gˡᵢⱼ on kerroksessa l olevien vektoroitujen ominaisuustietokarttojen i ja j välinen sisäinen tuote. Näemme, että Gˡᵢⱼ, joka on luotu tietyn kuvan ominaisuuskartan päälle, edustaa ominaisuuskarttojen i ja j välistä korrelaatiota.

Tyylien luomiseksi perussyötekuvallemme suoritamme gradienttilaskeutumisen sisältökuvasta muuttaaksemme sen kuvaksi, joka vastaa alkuperäisen kuvan tyyliesitystä. Teemme tämän minimoimalla tyylikuvan ja tulokuvan ominaisuuksien korrelaatiokartan välisen keskimääräisen neliöetäisyyden. Kunkin kerroksen osuutta kokonaistyylihäviöön kuvaa

jossa Gˡᵢⱼ ja Aˡᵢⱼ ovat sisääntulokuvan x:n ja tyylikuvan a:n tyylitietoedustuksen vastaavat tyylitietoedustustukset kerroksessa l. Nl kuvaa ominaisuuskarttojen lukumäärää, joista jokaisen koko on Ml=height∗width. Näin ollen tyylin kokonaishäviö kussakin kerroksessa on

jossa painotamme kunkin kerroksen häviön osuutta jollakin tekijällä wl. Meidän tapauksessamme painotamme jokaista kerrosta yhtä paljon:

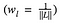
Tämä toteutetaan yksinkertaisesti:

Run Gradient Descent

Jos et tunne gradienttilaskeutumista/backpropagationia tai tarvitset kertausta, sinun kannattaa ehdottomasti tutustua tähän resurssiin.

Tässä tapauksessa käytämme Adam-optimoijaa tappion minimoimiseksi. Päivitämme iteratiivisesti ulostulokuvamme siten, että se minimoi tappiomme: emme päivitä verkkoomme liittyviä painoja, vaan sen sijaan koulutamme syöttökuvamme tappion minimoimiseksi. Tätä varten meidän on tiedettävä, miten laskemme häviömme ja gradienttimme. Huomaa, että L-BFGS-optimoija, jota suositellaan, jos olet perehtynyt tähän algoritmiin, mutta jota ei käytetä tässä opetusohjelmassa, koska tämän opetusohjelman ensisijainen motivaatio oli havainnollistaa parhaita käytäntöjä innokkaalla suorituksella. Käyttämällä Adamia voimme havainnollistaa autogradin/gradienttinauhan toiminnallisuutta mukautetuilla harjoittelusilmukoilla.

Häviön ja gradienttien laskeminen

Määrittelemme pienen apufunktion, joka lataa sisältö- ja tyylikuvamme, syöttää ne eteenpäin verkkoomme, joka sitten tulostaa sisällön ja tyylin ominaisuuksien esitystavat malleistamme.

Tässä käytämme gradientin laskemiseen tf.GradientTapea. Sen avulla voimme hyödyntää automaattista eriyttämistä, joka on käytettävissä jäljitysoperaatioiden avulla gradientin laskemiseksi myöhemmin. Se tallentaa operaatiot eteenpäinmenon aikana ja pystyy sitten laskemaan häviöfunktiomme gradientin suhteessa syötekuvaan taaksepäinmenoa varten.

Tällöin gradienttien laskeminen on helppoa:

Sovita ja suorita tyylinsiirtoprosessi

Ja tyylinsiirron varsinaiseen suorittamiseen:

Ja se on siinä!

Ajetaan se kilpikonnakuvallamme ja Hokusain teoksella Suuri aalto Kanagawan edustalla:

Katsele iteratiivista prosessia ajan myötä:

Tässä on muutama muu hieno esimerkki siitä, mitä neuraalinen tyylinsiirto voi tehdä. Check it out!

Kokeile omia kuvia!

Mitä käsiteltiin:

• Kehitimme useita erilaisia häviöfunktioita ja käytimme backpropagationia muuntaaksemme sisääntulokuvamme minimoidaksemme nämä häviöt.
• Tehdäksemme tämän latasimme sisään esiharjoittelemamme mallin ja käytimme sen oppimia ominaisuuskarttoja kuvaamaan kuviemme sisällön ja tyylin esittämistä.
• Tärkeimmät tappiofunktiomme olivat ensisijaisesti etäisyyden laskeminen näiden eri representaatioiden suhteen.
• Toteutimme tämän mukautetulla mallilla ja innokkaalla suorituksella.
• Rakensimme räätälöidyn mallimme Functional API:n avulla.
• Eager execution mahdollistaa dynaamisen työskentelyn tensoreiden kanssa käyttäen luonnollista pythonin kontrollivirtaa.
• Käsittelimme tensoreita suoraan, mikä helpottaa virheenkorjausta ja työskentelyä tensoreiden kanssa.

Päivitimme kuvamme iteratiivisesti soveltamalla optimoijien päivityssääntöjä tf.gradientin avulla. Optimoija minimoi annetut häviöt tulokuvamme suhteen.