Alai

Michael Fowler,UVa Physics.

Momentilla on suunta

Kuten edellisellä luennolla käsiteltiin, jo ennen kuin Newton muotoili lainalaisuutensa, Descartes oli Huygensin pienellä avustuksella havainnut syvällisen dynaamisen totuuden: missä tahansa törmäyksessä tai itse asiassa missä tahansa vuorovaikutuksessa ”momentin” – liikkeen mittarin – kokonaismäärä pysyy aina samana. Liikkuvan kappaleen impulssi määritellään massan ja nopeuden tulona, joten se on vektori: sillä on suuruus ja suunta. Jos seisot kitkattomilla luistimilla ja heität palloa, liikut taaksepäin: sinun momenttisi on yhtä suuri kuin pallon momentti, mutta vastakkaissuuntainen, joten kokonaismomentti (sinun momenttisi ja pallon momentti) pysyy nollassa. Raketit toimivat samalla tavalla heittämällä materiaalia ulos suurella nopeudella. Ne eivät toimi ”työntämällä ilmaa vasten”, vaan työntämällä ulos työntämäänsä ainetta vasten, aivan kuten työntämällä heittämääsi palloa vasten, jolloin se työntää sinua takaisin aiheuttaen kiihtyvyytesi.

Jos vielä epäilet, että oikeasti raketit työntävät ilmaa vastaan, muista, että ne toimivat yhtä hyvin avaruudessa! Itse asiassa yleisesti uskottiin, että kun Goddard, varhainen amerikkalainen rakettimies (Goddard Space Flight Center on nimetty hänen mukaansa) puhui raketeista avaruudessa, hän tuhlasi aikaansa. Lainaan New York Timesin pääkirjoitusta vuodelta 1921: ”Professori Goddard ei tunne toiminnan ja reaktion välistä suhdetta eikä sitä, että tarvitaan jotain tyhjiötä parempaa, jota vastaan reagoida. Häneltä näyttää puuttuvan se perustieto, jota lukioissamme päivittäin opetetaan.” Ilmeisesti New York Timesin silloiset pääkirjoittajat olivat perillä perustiedoista, joita tällä kurssilla jaettiin!

Tosiasiassa, kuten keskustelimme, momentin säilyminen törmäyksessä seuraa Newtonin laeista. Se on kuitenkin yleisempi, yksinkertaisempi käsite – se ei riipu lainkaan vuorovaikutusten yksityiskohdista jne. Tämä yksinkertaisuus ilmeisesti miellytti Einsteinia, joka oli vakuuttunut siitä, että kun dynamiikka muotoillaan uudelleen siten, että siihen sisällytetään uudet ajatukset ajasta ja avaruudesta, impulssin säilymisen pitäisi edelleen päteä missä tahansa inertiajärjestelmässä. Tämä johti hänet yllättäviin johtopäätöksiin, kuten tulemme näkemään.

Momentin säilyminen biljardipöydässä

Tarkastellaan lämmittelyharjoituksena momentin säilymistä kahden pallon törmäyksessä biljardipöydässä. Piirretään liituviiva biljardipöydän keskelle ja ammutaan pallot jommastakummasta päästä lähelle liituviivaa, mutta sen vastakkaisille puolille, samalla nopeudella, niin että ne osuvat keskelle viistosti, jolloin niiden nopeudet kääntyvät pienen kulman verran. Toisin sanoen, jos aluksi sanotaan, että niiden (yhtä suuret ja vastakkaissuuntaiset) nopeudet olivat x-suunnan – liitulinjan – suuntaisia, törmäyksen jälkeen niiden nopeudet ovat yhtä suuret ja vastakkaissuuntaiset myös y-suunnassa (x-suuntaiset nopeudet ovat pienentyneet hyvin vähän).

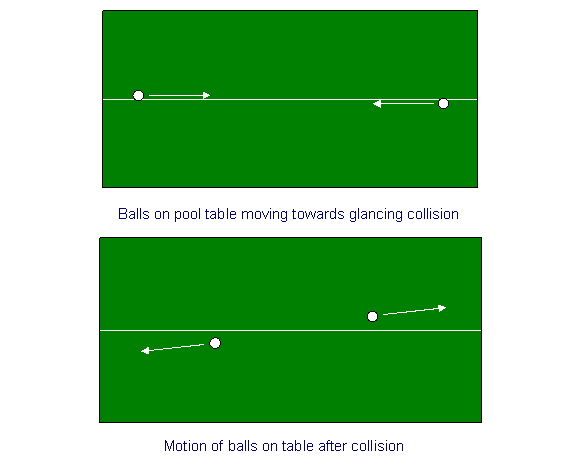
Symmetrinen avaruusaluksen törmäys

Nyt toistetaan harjoitus suuressa mittakaavassa. Oletetaan, että jossain avaruudessa, kaukana kaikista gravitaatiokentistä, asetetaan miljoona mailia pitkä säie. (Se voisi olla kahden kellomme välissä ajanlaajennuskokeessa). Tämä merkkijono vastaa biljardipöydän liituviivaa. Oletetaan nyt, että meillä on kaksi identtistä avaruusalusta, jotka lähestyvät toisiaan yhtä suurilla ja vastakkaisilla nopeuksilla jousen suuntaisesti jousen molemmista päistä ja jotka on suunnattu siten, että ne törmäävät hieman loivasti, kun ne kohtaavat keskellä. Tilanteen symmetrisyydestä seuraa, että momentti säilyy molempiin suuntiin. Erityisesti nopeus, jolla toinen avaruusalus etääntyy jousesta törmäyksen jälkeen – sen y-nopeus – on yhtä suuri ja vastakkainen kuin nopeus, jolla toinen alus etääntyy jousesta.

Mutta nyt tarkastellaan tätä törmäystä jonkun havainnoimana, joka on jossakin avaruusaluksista, sanotaan se A. Ennen törmäystä hän näkee jousen liikkuvan hyvin nopeasti ikkunan vieressä, vaikkapa muutaman metrin päässä. Törmäyksen jälkeen hän näkee säikeen liikkuvan poispäin, vaikkapa 15 metriä sekunnissa. Tämä johtuu siitä, että avaruusalus A:n nopeus kohtisuoraan janoon nähden on 15 metriä sekunnissa. Koska tilanne on täysin symmetrinen, avaruusalus B:ssä oleva havaitsija päättelisi varmasti, että myös hänen avaruusaluksensa liikkuu poispäin jousesta 15 metriä sekunnissa.

Kuinka symmetristä se on?

Kriittinen kysymys on: kuinka nopeasti avaruusalus A:n inspiroima havaitsija näkee avaruusalus B:n liikkuvan poispäin jousesta? Oletetaan, että avaruusalus A:han nähden avaruusalus B liikkuu poispäin (x-suunnassa) 0,6c:n nopeudella. Muistutetaan ensin, että liikesuuntaa vastaan kohtisuorassa olevat etäisyydet eivät ole Lorentzin supistamia. Näin ollen, kun avaruusalus B:ssä oleva havaitsija sanoo siirtyneensä 15 metriä kauemmas jousesta yhden sekunnin välein, avaruusalus A:sta tätä liikettä seuraava havaitsija on samaa mieltä 15 metristä – mutta eri mieltä yhdestä sekunnista! Hän sanoo, että hänen kellonsa käyvät hitaasti, joten hänen kellojensa mukaan mitattuna on kulunut 1,25 sekuntia, kun nainen liikkuu 15 metriä y-suunnassa.

Tästä seuraa, että aikadilataation seurauksena tämä törmäys avaruusalus A:sta katsottuna ei aiheuta molemmille avaruusaluksille yhtä suuria ja vastakkaisia nopeuksia y-suunnassa. Aluksi molemmat avaruusalukset liikkuivat x-akselin suuntaisesti, y-suunnassa oli nollavoima. Miten voimme siis väittää, että törmäyksen jälkeen y-suunnassa on nolla kokonaisimpulssia, kun identtisillä avaruusaluksilla ei ole yhtä suuria ja vastakkaisia nopeuksia?

Einstein pelastaa momentin säilymisen

Einstein oli niin varma, että momentin säilymisen täytyy aina päteä, että hän pelasti sen rohkealla hypoteesilla: kappaleen massan täytyy riippua sen nopeudesta! Itse asiassa massan on kasvettava nopeuden myötä juuri siten, että se kumoaa ajanlaajenemisesta johtuvan y-suunnan pienemmän nopeuden. Toisin sanoen, jos levossa olevalla kappaleella on massa m, kun se liikkuu nopeudella v, sillä on inertia, joka vastaa ”relativistista massaa” m rel =m/ 1-( v 2 / c 2 ) Tällöin momentti on

p → = m rel v → =m v → / 1-( v 2 / c 2 ) .

Huomaa, että tämä relativistinen massan lisäys on tavallisilla nopeuksilla huomaamattoman pieni vaikutus, mutta kun kappale lähestyy lentonopeutta, massa kasvaa rajattomasti!

Massa todella kasvaa nopeuden myötä

Päätöksellä, että kappaleiden massojen täytyy riippua nopeudesta näin näyttää olevan kova hinta liikemäärän säilymisen pelastamiseksi! Se on kuitenkin ennuste, jota ei ole vaikea tarkistaa kokeellisesti. Ensimmäinen vahvistus saatiin vuonna 1908 poikkeuttamalla nopeita elektroneja tyhjiöputkessa. Vanhantyylisessä väritelevisioputkessa olevilla elektroneilla on itse asiassa noin puoli prosenttia enemmän inertiaa kuin lepotilassa olevilla elektroneilla, ja tämä on otettava huomioon laskettaessa magneettikenttiä, joita käytetään niiden ohjaamiseen näytölle.

Paljon dramaattisemmin nykyaikaisissa hiukkaskiihdyttimissä käytetään erittäin voimakkaita sähkökenttiä elektronien, protonien ja muiden hiukkasten kiihdyttämiseen. Käytännössä on havaittu, että nämä hiukkaset tarvitsevat yhä suurempia voimia kiihdyttääkseen niitä edelleen, kun valon nopeutta lähestytään. Näin ollen valonnopeus on luonnollinen absoluuttinen nopeusraja. Hiukkasia kiihdytetään nopeuksiin, joissa niiden relativistinen massa on tuhansia kertoja suurempi kuin niiden lepotilassa mitattu massa, jota yleensä kutsutaan lepomassaksi.

…Vai onko?

Fyysikot käyvät jatkuvasti keskustelua tästä relativistisen massan käsitteestä. Väittely on pitkälti semanttista: kukaan ei epäile, etteikö nopeudella v → liikkuvan hiukkasen, jolla on lepomassa m, impulssin oikea lauseke olisi p → = m 1- v 2 / c 2 v → . Mutta erityisesti hiukkasfyysikot, joista monet viettävät elämänsä mittaamalla hiukkasten lepomassoja suurella tarkkuudella, eivät ole innokkaita kirjoittamaan tätä muotoon p → = m rel v → . He eivät pidä ajatuksesta muuttuvasta massasta. Ensinnäkin se saattaa antaa sen vaikutelman, että hiukkanen paisuu nopeutuessaan tai ainakin sen sisäinen rakenne muuttuu jotenkin. Itse asiassa relativistinen hiukkanen vain supistuu Lorentzin vaikutuksesta liikesuunnassa, kuten mikä tahansa muukin. Se muuttuu pallomaisesta muodosta kohti kiekkomaista muotoa, jolla on sama poikittaissäde.

Miten tämä ”massan kasvu” sitten voidaan ymmärtää? Kuten tavallista,Einstein oli oikeassa: hän huomautti, että kaikilla energian muodoilla on inertia. Kineettisellä energialla itsellään on inertia. Nyt ”inertia” on massan määrittelevä ominaisuus. Toinen massan perusominaisuus on, että se vetää puoleensa painovoimaisesti. Tekeekö tämä liike-energia niin? Vastauksen saamiseksi tarkastellaan kaasulla täytettyä palloa. Se synnyttää itsensä ulkopuolella pallosymmetrisen gravitaatiokentän, jonka voimakkuus on verrannollinen kokonaismassaan. Jos kaasua nyt lämmitetään, kaasuhiukkasilla on lisääntynyt (relativistinen) massa, joka vastaa niiden lisääntynyttä liike-energiaa, ja ulkoinen gravitaatiokenttä on kasvanut samassa suhteessa. (Kukaan ei epäile kumpaakaan.)

”Relativistisella massalla” on siis todellakin kaksi massan perusominaisuutta: inertia ja gravitaatiovetovoima. (Kuten seuraavilla luennoilla selviää, tämä relativistinen massa ei ole mitään muuta kuin kokonaisenergiaa,jolloin lepomassaa itsessään pidetään nyt energiana.)

Triviaalimmalla tasolla jotkut opettajat vastustavat relativistisen massan käyttöönottoa, koska he pelkäävät, että oppilaat olettavat relativistisesti liikkuvan hiukkasen liike-energian olevan vain 1 2 m m v → 2 relativistisen massan avulla – näin ei ole,kuten pian nähdään.

Jalkahuomautus: Niille, jotka saattavat joskus siirtyä matemaattisesti hienostuneempaan käsittelyyn, on lisättävä, että lepomassalla on tärkeä rooli invarianttina siirryttäessä yhdestä viitekehyksestä toiseen, mutta tässä käytetty ”relativistinen massa” on oikeastaan vain hiukkasen neliulotteisen energia-momenttivektorin ensimmäinen komponentti (energia), joten se ei ole invariantti.

Kineettinen energia ja massa hyvin nopeille hiukkasille

Ajatellaanpa yhden tällaisen lähellä valonnopeutta kulkevan hiukkasen kineettistä energiaa. Muistetaan, että aiemmalla luennolla havaittiin, että tavallisen ei-relativistisen (eli hitaasti liikkuvan) massan m liike-energia oli 1 2 m v 2 . Tämän saimme selville tarkastelemalla, kuinka paljon työtä jouduimme tekemään sen nostamiseksi tietylle korkeudelle: jouduimme käyttämään sen painon W suuruista voimaa nostaaksemme sen korkeudelle h. Kokonaisuudessaan tehty työ tai kulutettu energia on voima x etäisyys, Wh. Kun kappale putosi takaisin alas, painovoima W teki putoavaan kappaleeseen täsmälleen saman verran työtä Wh, mutta tällä kertaa työ meni kappaleen kiihdyttämiseen ja antoi sille liike-energiaa. Koska tiedämme, kuinka nopeasti putoavat kappaleet ottavat nopeutta, voimme päätellä, että liike-energia oli 1 2 m v 2 . (Ks. tarkemmin edelliseltä luennolta.)

Yleisemmin olisimme voineet kiihdyttää massaa millä tahansa vakiovoimalla F ja löytää voiman tekemän työn (voima x etäisyys), jotta se olisi saanut nopeuden v pysähtyneestä lähtötilanteesta. Massan liike-energia, E= 1 2 m v 2 , on täsmälleen yhtä suuri kuin voiman tekemä työ massan saattamiseksi kyseiseen nopeuteen. (Vastaavasti voidaan osoittaa, että jos jo vaikkapa nopeudella u liikkuvaan hiukkaseen kohdistetaan voima ja se kiihdytetään nopeuteen v, tarvittava työ on 1 2 m v 2 – 1 2 m u 2 ).

On mielenkiintoista yrittää toistaa harjoitus hiukkaselle, joka liikkuu hyvin lähellä valon nopeutta, kuten edellisessä kappaleessa mainituissa kiihdyttimissä olevat hiukkaset. Newtonin toinen laki muodossa

Voima = liikemäärän muutosnopeus

pitää edelleen paikkansa, mutta lähellä valonnopeutta nopeus muuttuu mitättömän vähän voiman jatkaessa toimintaansa – sen sijaan massa kasvaa! Siksi voimme kirjoittaa erinomaisella approksimaatiolla:

Voima = (massan muutosnopeus) x c

joissa c on tavalliseen tapaan valonnopeus. Tarkemmin sanottuna oletetaan, että meillä on vakiovoima F, joka työntää hiukkasta. Jossain vaiheessa hiukkasella on massa M ja nopeus on äärimmäisen lähellä c:tä. Sekuntia myöhemmin, koska voima jatkaa hiukkaseen kohdistuvaa työtä ja siten lisää sen impulssia Newtonin toisen lain mukaisesti, hiukkasella on massa M+m, jossa m on voiman tekemän työn aiheuttama massan lisäys.

Mikä on hiukkasen liike-energian E kasvu tuon yhden sekunnin jakson aikana? Täsmällisessä analogiassa edellä tarkastellun ei-relativistisen tapauksen kanssa se on vain voiman tekemä työ tuon ajanjakson aikana. Koska hiukkasen massa muuttuu sekunnissa m, m on myös massan muutosnopeus. Näin ollen Newtonin toisen lain muodossa

voima = (massan muutosnopeus) x c,

voimme kirjoittaa

voima =mc.

Kineettisen energian E kasvu sekunnin aikana on vain voiman tekemä työ,

E=voima x matka.

Sen vuoksi, että hiukkanen liikkuu olennaisesti lentonopeudella, matka, jolla voima vaikuttaa sekunnin aikana, on vain c metriä, c=3× 10 8 .

Siten voiman tuossa sekunnissa tekemä kokonaistyö on voima x etäisyys =mc×c=m c 2 .

Lativistisen hiukkasen massan kasvun ja liike-energian kasvun välinen suhde on siis:

E=m c 2 .

Kineettinen energia ja massa hitaille hiukkasille

Muistutetaan, että jotta Newtonin lait voisivat päteä kaikissa inertiaalikehyksissä, oli oletettava massan kasvavan nopeuden myötä kertoimella 1/ 1-( v 2 / c 2 ) . Tämä merkitsee sitä, että hitaasti liikkuvankin kappaleen massa kasvaa vain vähän sen liikkuessa!

Miten tämä pieni lisäys liittyy liike-energiaan? Tarkastellaan massaa M, joka liikkuu nopeudella v, joka on paljon pienempi kuin valonnopeus. Sen liike-energia E= 1 2 M v 2 , kuten edellä käsiteltiin. Sen massa on M/ 1-( v 2 / c 2 ) , joka voidaan kirjoittaa muotoon M+m. Mikä on m ?

Koska puhumme meille tutuista nopeuksista, kuten suihkukoneesta, jossa v/c, on todella pieni, voimme käyttää joitakin yksinkertaisia matemaattisia temppuja asian helpottamiseksi.

Ensimmäinen on hyvä approksimaatio 1-x:n neliöjuurelle, kun x on paljon pienempi kuin yksi:

1-x ≅1- 1 2 x varten x≪1.

Voit helposti tarkistaa tämän laskimellasi: kokeile x= 1 100 , saat tulokseksi 99 100 =0,994987… joka on erittäin lähellä 1- 1 2 1 100 =0,995 !

Seuraava approksimaatio on

1 1-x ≅1+x for x≪1.

Tämä on myös helppo tarkistaa: otetaan taas x= 1 100 : 1 1-x = 1 99 100 = 100 99 =1.01010… ,ja 1+x= 101 100 =1.01.

Käyttäen näitä approksimaatioita x=v/c, voimme approksimoida 1-( v 2 / c 2 ) 1- 1 2 ( v 2 / c 2 ) ,ja sitten 1/( 1- 1 2 ( v 2 / c 2 ) ) ) 1+ 1 2 ( v 2 / c 2 ) .

Tämä tarkoittaa, että kokonaismassa nopeudella v

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ) ),

ja kirjoittamalla tämä muotoon M+m nähdään, että massan lisäys m on yhtä suuri kuin 1 2 M v 2 / c 2 .

Tämä tarkoittaa, että – jälleen kerran – massanlisäys m liittyy liike-energiaan E kaavalla E=m c 2 .

Itse asiassa ei ole vaikea osoittaa pienellä laskutoimituksella, että koko nopeusalueella nollasta mahdollisimman lähelle valonnopeutta liikkuva hiukkanen kokee massan lisäyksen, joka on verrannollinen sen liike-energiaan E=m c 2 . Ymmärtääksesi, miksi tätä ei huomata jokapäiväisessä elämässä, kokeile esimerkkiä, kuten 100 tonnia painavaa suihkukonetta, joka liikkuu 2 000 mailin tuntinopeudella. 100 tonnia on 100 000 kilogrammaa, 2 000mph on noin 1 000 metriä sekunnissa. Tämä on kineettistä energiaa 1 2 M v 2 ½ × 1011 joulea, mutta lentokoneen vastaava massanmuutos pienenee kertoimella c 2 , 9 × 10 16, jolloin todellinen massanlisäys on noin puoli milligrammaa, mikä ei ole kovin helppo havaita!

E = mc2

Edellä nähtiin, että kun voima tekee työtä kiihdyttääkseen kappaletta ja antaakseen sille liike-energiaa, kappaleen massa kasvaa määrällä, joka on yhtä suuri kuin voiman tekemä kokonaistyö, siirretty energia E jaettuna c 2 :lla. Entä kun voima tekee työtä kappaleeseen, joka ei kiihdytä sitä, jolloin liike-energia ei kasva? Entä jos esimerkiksi nostan jotakin tasaisella nopeudella ja annan sille potentiaalienergiaa? Osoittautuu, että tässäkin tapauksessa massa kasvaa E=m c 2 :n mukaisesti, mikä on tietenkin mittaamattoman pieni jokapäiväisille esineille.

Tämä on kuitenkin mitattavissa oleva ja tärkeä vaikutus ydinfysiikassa. Esimerkiksi heliumatomin ytimessä on kaksi protonia ja kaksi neutronia, jotka on sidottu toisiinsa hyvin tiukasti vahvalla ydinvetovoimalla. Jos ulkoista voimaa käytetään riittävästi, se voidaan erottaa kahdeksi ”raskaaksi vetyytimeksi”, joissa kummassakin on yksi protoni ja yksi neutroni. Tämän erottelun aikaansaamiseksi on käytettävä paljon ulkoista energiaa, ja havaitaan, että kahden raskaan vetyytimen kokonaismassa on mitattavasti (noin puoli prosenttia) raskaampi kuin alkuperäisen heliumytimen massa. Tämä ylimääräinen massa kerrottuna c 2 :llä vastaa juuri sitä energiaa, joka tarvitaan heliumytimen jakamiseen kahtia. Vielä tärkeämpää on, että tämä energia voidaan ottaa talteen antamalla kahden raskaan vesiytimen törmätä toisiinsa ja yhdistyä uudelleen heliumytimeksi. (Molemmat ytimet ovat sähköisesti positiivisesti varattuja, joten ne hylkivät toisiaan, ja niiden on liityttävä toisiinsa melko nopeasti, jotta ne voivat voittaa tämän hylkimisen ja päästä niin lähelle toisiaan, että paljon voimakkaampi ydinvetovoima alkaa vaikuttaa). Tämä on vetypommin ja auringon perusvoimanlähde.

On käynyt ilmi, että kaikkiin energiamuotoihin, liike-energiaan ja erilaisiin potentiaalienergioihin, liittyy massa, joka saadaan kaavalla E=m c 2 . Ydinreaktioissa massanmuutos on tyypillisesti suuruusluokkaa tuhannesosa kokonaismassasta ja helposti mitattavissa. Kemiallisissa reaktioissa muutos on suuruusluokkaa miljardisosa kokonaismassasta, eikä se ole tällä hetkellä mitattavissa.

edellinen indeksi