Csoportok szorzása
Most azt fogjuk megvizsgálni, mi történik, ha két szimmetriaműveletet egymás után alkalmazunk. Példaként tekintsük a \(NH_3\) molekulát, amely a \(C_{3v}\) pontcsoportba tartozik. Nézzük meg, mi történik, ha egy \(C_3\)-forgatást \(\sigma_v\) tükrözés követ. Ezt a kombinált műveletet \(\sigma_v\)\(C_3\)-nek írjuk (a szimmetriaműveletek a tőlük közvetlenül jobbra lévő dologra hatnak, ahogy az operátorok a kvantummechanikában – ezért a jelölésből jobbról balra visszafelé kell haladnunk, hogy megkapjuk a helyes sorrendet, amelyben az operátorokat alkalmazzuk). Mint hamarosan látni fogjuk, a műveletek alkalmazásának sorrendje fontos.
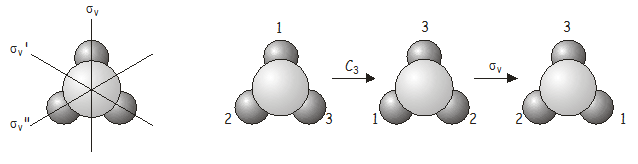
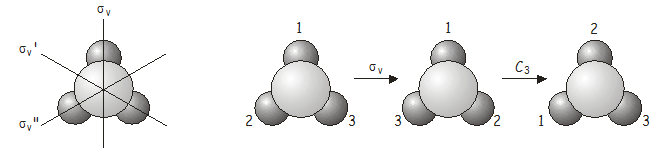
Az \(C_3\)\(\sigma_v\) kombinált művelet ekvivalens a pontcsoport egy másik műveletével, ezúttal \(\sigma_v’\).
Ez a példa két fontos dolgot mutat be:
Az adott pontcsoporton belül két szimmetriaművelet egymás utáni alkalmazásának hatásait a csoportszorzási táblázatokban foglaljuk össze. Példaként a \(C_{3v}\) teljes csoportszorzási táblázata a fenti ábrákon meghatározott szimmetriaműveletek alkalmazásával az alábbiakban látható. A táblázat első sorában írt műveleteket hajtjuk végre először, majd az első oszlopban írtakat (megjegyezzük, hogy a táblázat megváltozna, ha a \(\sigma_v\), \(\sigma_v’\) és \(\sigma_v”\) neveket más sorrendben adnánk meg).