
update : Bevezettünk egy interaktív tanulási alkalmazást gépi tanuláshoz / AI ,>> Nézd meg most ingyen <<
Importáld a szükséges könyvtárakat
import numpy as np
import pandas as pd
eps = np.finfo(float).eps
from numpy import log2 as log
‘eps’ itt a legkisebb ábrázolható szám. Időnként log(0) vagy 0-t kapunk a nevezőben, ennek elkerülésére ezt fogjuk használni.
Adatkészlet definiálása:
Pandas adatkeret létrehozása :
Most próbáljuk meg megjegyezni a döntési fa létrehozásának lépéseit…..
1.compute the entropy for data-set2.for every attribute/feature:
1.calculate entropy for all categorical values
2.take average information entropy for the current attribute
3.calculate gain for the current attribute3. pick the highest gain attribute.
4. Repeat until we get the tree we desired
- keressük meg az entrópiát, majd az információnyereséget az adathalmaz felosztásához.
Meghatározunk egy olyan függvényt, amely felveszi az osztályt (célváltozó vektor) és megtalálja az adott osztály entrópiáját.
Itt a tört ‘pi’, ez az adott osztott csoportban lévő elemek számának aránya az osztás előtti csoportban lévő elemek számához(szülőcsoport).

2 kaptunk.Most definiáljunk egy {ent} függvényt az egyes attribútumok entrópiájának kiszámításához :
tároljuk az egyes attribútumok entrópiáját a nevükkel :
a_entropy = {k:ent(df,k) for k in df.keys()}
a_entropy

3. Minden attribútum infónyereségének kiszámítása :
definiáljunk egy függvényt az IG (infónyereség) kiszámítására :
IG(attr) = adathalmaz entrópiája – attribútum entrópiája
def ig(e_dataset,e_attr):
return(e_dataset-e_attr)
minden attr IG-jét egy dict-ben tároljuk :
#entropy_node = entropy of dataset
#a_entropy = entropy of k(th) attrIG = {k:ig(entropy_node,a_entropy) for k in a_entropy}

mint láthatjuk a kilátásoknak van a legnagyobb információnyeresége, 0.24 , ezért ezen a szinten outook-ot választjuk csomópontnak a felosztáshoz.
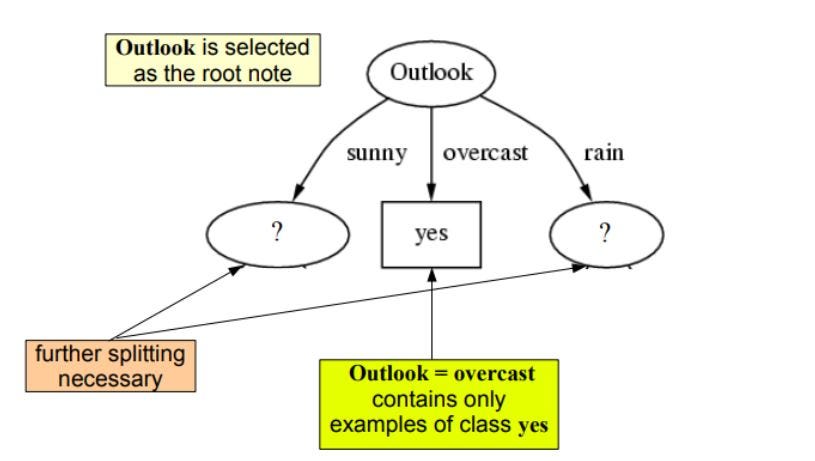
Most a fánk folytatásához rekurziót fogunk használni
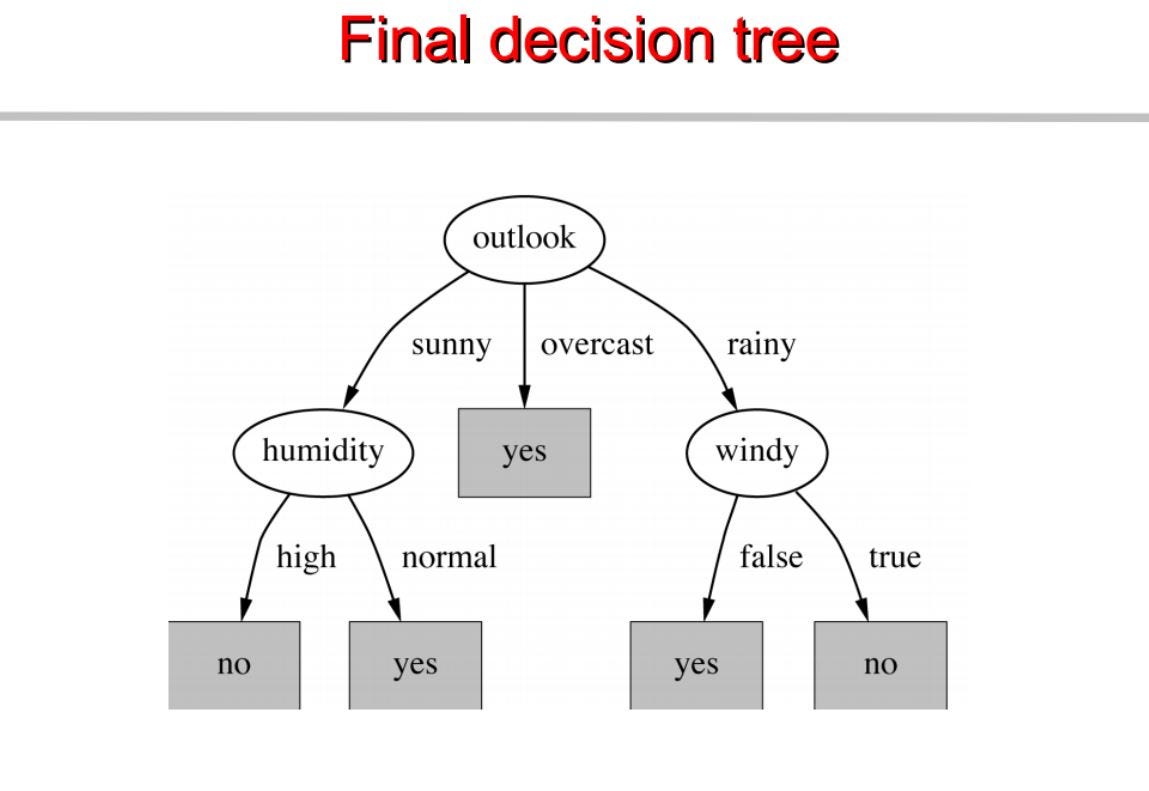
Megismételjük ugyanezt az alfáknál, amíg meg nem kapjuk a fát.

Ez alapján építünk egy döntési fát. Alább a teljes kód.

látogasson el a pytholabs.com oldalra a csodálatos kurzusokért
.