A robusztus statisztika alábbi definíciója P. J. Huber Robust Statistics című könyvéből származik.
… bármely statisztikai eljárásnak a következő kívánatos tulajdonságokkal kell rendelkeznie:
- Megfelelően jó (optimális vagy közel optimális) hatékonysággal kell rendelkeznie a feltételezett modell mellett.
- Robusztusnak kell lennie abban az értelemben, hogy a modellfeltevésektől való kis eltérések csak kis mértékben rontják a teljesítményt. …
- A modelltől való némileg nagyobb eltérések nem okozhatnak katasztrófát.
A klasszikus statisztika Huber első pontjára összpontosít, és olyan módszereket hoz létre, amelyek bizonyos kritériumok mellett optimálisak. Ez a bejegyzés a Huber második és harmadik pontjának illusztrálására használt kanonikus példákat vizsgálja.
Huber harmadik pontját jellemzően a minta átlaga (átlag) és a minta mediánja (középérték) illusztrálja. A minta adatainak majdnem felét ∞-re állíthatjuk anélkül, hogy a minta mediánja végtelenné válna. A mintaátlag viszont végtelenné válik, ha bármelyik mintaérték végtelen. A modelltől való nagy eltérések, azaz néhány kiugró érték katasztrófát okozhat a mintaátlagra, de a minta mediánjára nem.”
A kanonikus példa Huber második pontjának tárgyalásakor John Tukey-ra vezethető vissza. Kezdjük a becslés legegyszerűbb tankönyvi példájával: ismeretlen átlagú és 1 szórású normális eloszlásból származó adatok, azaz az adatok normal(μ, 1), μ ismeretlen. A μ becslésének leghatékonyabb módja, ha a mintaátlagot, az adatok átlagát vesszük.
De most tegyük fel, hogy az adatok eloszlása nem pontosan normal(μ, 1), hanem egy standard normáleloszlás és egy eltérő szórású normáleloszlás keveréke. Legyen δ egy kis szám, mondjuk 0,01, és tegyük fel, hogy az adatok 1-δ valószínűséggel normál(μ, 1) eloszlásból származnak, az adatok pedig δ valószínűséggel normál(μ, σ2) eloszlásból származnak. Ezt az eloszlást “szennyezett normálnak” nevezzük, és a δ szám a szennyezettség mértéke. A szennyezett normális modell használatának oka, hogy ez egy nem normális eloszlás, amely szemmel nézve normálisnak tűnhet.
A populáció μ átlagát vagy a minta átlaga, vagy a minta mediánja segítségével becsülhetjük meg. Ha az adatok nem keverék, hanem szigorúan normálisak lennének, akkor a mintaátlag lenne a μ leghatékonyabb becslője. Ebben az esetben a standard hiba körülbelül 25%-kal nagyobb lenne, ha a minta mediánját használnánk. Ha azonban az adatok keverékből származnak, akkor a minta mediánja hatékonyabb lehet, a δ és σ méretétől függően. Íme a minta mediánjának ARE (aszimptotikus relatív hatékonyság) ábrája a minta középértékéhez képest σ függvényében, amikor δ = 0. Ez a minta mediánja és a minta középértéke közötti különbség.01.
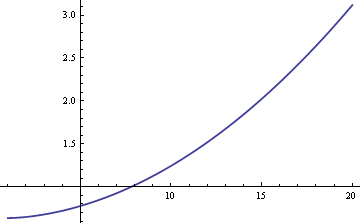
A grafikon azt mutatja, hogy σ 8-nál nagyobb értékei esetén a minta mediánja hatékonyabb, mint a minta átlaga. A medián relatív fölénye a σ növekedésével korlátlanul növekszik.
Itt van az ARE ábrája σ 10-re rögzített értékkel és δ 0 és 1 között változó értékkel.
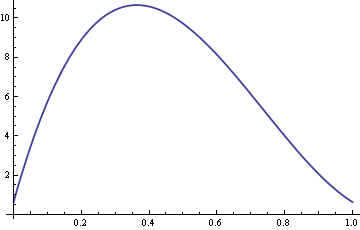
A δ 0 körüli értékei esetén tehát.4 értékeknél a minta mediánja több mint tízszer hatékonyabb, mint a minta átlaga.
Az ARE általános képlete ebben a példában 2((1 + δ(σ2 – 1)(1 – δ + δ/σ)2)/ π.
Ha biztosak vagyunk abban, hogy az adataink normálisak, szennyeződés nélkül vagy nagyon kevés szennyeződéssel, akkor a minta átlaga a leghatékonyabb becslő. De lehet, hogy érdemes megkockáztatni, hogy lemondunk egy kis hatékonyságról, cserébe azért a tudatért, hogy jelentős szennyeződés esetén jobban fogunk járni egy robusztus modellel. Jelentős szennyeződés esetén nagyobb veszteséget okozhat a mintaátlag használata, mint potenciális nyereséget a mintaátlag használata, ha nincs szennyeződés.
Itt van egy rejtély a szennyezett normál példával kapcsolatban. Normál(μ, 1) adatokra a leghatékonyabb becslő a mintaátlag. És a leghatékonyabb becslő normál(μ, σ2) adatokra szintén a mintaátlag. Akkor miért nem optimális a keverék mintaátlagát venni?
A kulcs az, hogy nem tudjuk, hogy egy adott minta a normál(μ, 1) eloszlásból vagy a normál(μ, σ2) eloszlásból származik. Ha tudnánk, akkor szétválogathatnánk a mintákat, külön-külön átlagolhatnánk őket, és a mintákat összevonhatnánk egy összesített átlagba: az egyik átlagot megszorozzuk 1-δ-vel, a másikat δ-vel, és összeadjuk. De mivel nem tudjuk, hogy a keverék mely összetevői milyen mintákhoz vezetnek, nem tudjuk megfelelően súlyozni a mintákat. (Valószínűleg a δ-t sem ismerjük, de ez már más kérdés.)
A mintaátlag vagy a minta mediánjának használatán kívül más lehetőségek is vannak. Például a trimmelt átlag kidob néhányat a legnagyobb és legkisebb értékek közül, majd minden mást átlagol. (Néha a sportok is így működnek, kidobják egy sportoló legmagasabb és legalacsonyabb pontszámát a bírók.) Minél több adatot dobunk ki mindkét végén, annál inkább úgy viselkedik a rövidített átlag, mint a minta mediánja. Minél kevesebb adatot dobunk ki, annál inkább úgy viselkedik, mint a minta átlaga.
Kapcsolódó bejegyzés:
Napi adattudományi tippekért kövesse a @DataSciFact-ot a Twitteren.
.