Alai

By Raymond Yuan, Szoftverfejlesztő gyakornok

Ezzel a bemutatóval megtanuljuk, hogyan használhatjuk a mély tanulást arra, hogy képeket komponáljunk egy másik kép stílusában (vágytál már arra, hogy úgy fess, mint Picasso vagy Van Gogh?). Ez az úgynevezett neurális stílustranszfer! Ezt a technikát Leon A. Gatys A Neural Algorithm of Artistic Style című tanulmányában vázolja fel, amely remek olvasmány, és mindenképpen érdemes megnézni.

A neurális stílustranszfer egy optimalizációs technika, amelyet három kép – egy tartalmi kép, egy stílusreferenciakép (például egy híres festő műalkotása) és a stilizálni kívánt bemeneti kép – összemosására használunk, hogy a bemeneti kép úgy alakuljon át, hogy úgy nézzen ki, mint a tartalmi kép, de a stíluskép stílusában “festve”.

Vegyünk például egy képet erről a teknősről és Katsushika Hokusai A nagy hullám Kanagawa előtt című művéről:

Most hogy nézne ki, ha Hokusai úgy döntene, hogy a hullámok textúráját vagy stílusát hozzáadja a teknős képéhez? Valami ilyesmi?

Ez varázslat vagy csak mélytanulás? Szerencsére nem varázslatról van szó: a stílusátvitel egy szórakoztató és érdekes technika, amely bemutatja a neurális hálózatok képességeit és belső reprezentációit.

A neurális stílusátvitel elve az, hogy két távolságfüggvényt definiálunk: az egyik azt írja le, hogy mennyire különbözik két kép tartalma, Lcontent, a másik pedig a két kép közötti különbséget a stílusuk szempontjából, Lstyle. Ezután három képet, egy kívánt stílusképet, egy kívánt tartalomképet és a bemeneti képet (inicializálva a tartalomképpel) megadva megpróbáljuk úgy átalakítani a bemeneti képet, hogy minimalizáljuk a tartalmi távolságot a tartalomképpel és a stílus távolságát a stílusképpel.

Összefoglalva, vesszük az alap bemeneti képet, egy tartalmi képet, amelyet meg akarunk egyezni, és a stílusképet, amelyet meg akarunk egyezni. Az alap bemeneti képet úgy alakítjuk át, hogy a tartalom és a stílus távolságát (veszteségeit) backpropagációval minimalizáljuk, és létrehozunk egy olyan képet, amely megfelel a tartalomkép tartalmának és a stíluskép stílusának.

A folyamat során gyakorlati tapasztalatokat szerzünk és intuíciót fejlesztünk a következő fogalmakkal kapcsolatban:

• Eager Execution – a TensorFlow imperatív programozási környezetének használata, amely azonnal kiértékeli a műveleteket
• Tudjunk meg többet az eager executionről
• Nézzük meg a gyakorlatban (sok oktatóprogram futtatható a Colaboratoryban)
• Functional API használata a modell definiálásához – felépítjük a modellünk egy részhalmazát, amely hozzáférést biztosít számunkra a szükséges köztes aktiválásokhoz a Functional API segítségével
• Előre betanított modell tulajdonságtérképének kihasználása – megtanuljuk, hogyan használjuk az előre betanított modelleket és azok tulajdonságtérképeit
• Egyéni tréninghurkok létrehozása – megvizsgáljuk, hogyan állíthatunk be egy optimalizálót egy adott veszteség minimalizálására a bemeneti paraméterek tekintetében

A stílusátvitel általános lépéseit követjük:

1. Visualize data
2. Basic Preprocessing/prepareing our data
3. Set up loss functions
4. Create model
5. Optimize for loss function

Audience: Ez a bejegyzés olyan középhaladó felhasználóknak szól, akik jól ismerik a gépi tanulás alapfogalmait. Ahhoz, hogy a legtöbbet hozza ki ebből a posztból, érdemes:

• Elolvasni Gatys cikkét – mi majd menet közben elmagyarázzuk, de a cikk alaposabb megértést nyújt a feladatról
• A gradiens ereszkedés megértése

A becsült idő: 60 perc

Kód:

A cikk teljes kódját ezen a linken találod. Ha szeretné lépésről lépésre végigvenni ezt a példát, itt találja a colabot.

Implementáció

Azzal kezdjük, hogy engedélyezzük a buzgó végrehajtást. A buzgó végrehajtás lehetővé teszi, hogy a legegyértelműbben és legolvashatóbban dolgozzuk fel ezt a technikát.

Define content and style representations

Hogy megkapjuk a képünk tartalmi és stílusbeli reprezentációját is, megnézünk néhány köztes réteget a modellünkön belül. A köztes rétegek olyan jellemzőtérképeket képviselnek, amelyek egyre magasabb rendűvé válnak, ahogy mélyebbre megyünk. Ebben az esetben a VGG19 hálózati architektúrát használjuk, amely egy előre betanított képosztályozó hálózat. Ezek a köztes rétegek szükségesek ahhoz, hogy meghatározzuk a tartalom és a stílus reprezentációját a képeinkből. Egy bemeneti kép esetében megpróbáljuk megfeleltetni a megfelelő stílus és tartalom célreprezentációkat ezeken a köztes rétegeken.

Miért köztes rétegek?

Elgondolkodhat azon, hogy miért ezek a köztes kimenetek az előgyakorolt képosztályozó hálózatunkon belül lehetővé teszik számunkra a stílus és a tartalom reprezentációinak meghatározását. Magas szinten ez a jelenség azzal magyarázható, hogy ahhoz, hogy egy hálózat képosztályozást végezzen (amire a mi hálózatunkat betanítottuk), meg kell értenie a képet. Ez azt jelenti, hogy a nyers képet bemeneti képpontokként veszi, és transzformációkon keresztül felépít egy belső reprezentációt, amely a nyers képpontokat a képben jelen lévő jellemzők komplex megértésévé alakítja. Részben ezért is képesek a konvolúciós neurális hálózatok jól általánosítani: képesek megragadni az osztályokon belüli invarianciákat és meghatározó jellemzőket (pl. macskák vs. kutyák), amelyek a háttérzajtól és egyéb zavaró tényezőktől függetlenek. Így valahol a nyers kép betáplálása és az osztályozási címke kimenete között a modell komplex jellemző-kivonatként szolgál; így a köztes rétegek elérésével képesek vagyunk leírni a bemeneti képek tartalmát és stílusát.

Kifejezetten ezeket a köztes rétegeket fogjuk kihúzni a hálózatunkból:

Modell

Ez esetben betöltjük a VGG19-et, és betápláljuk a bemeneti tenzorunkat a modellbe. Ez lehetővé teszi számunkra, hogy kivonjuk a tartalom, a stílus és a generált képek tulajdonságtérképeit (és később a tartalom és a stílus reprezentációit).

A VGG19-et használjuk, ahogy azt a tanulmányban javasoltuk. Ráadásul mivel a VGG19 egy viszonylag egyszerű modell (a ResNet, Inception stb. modellekhez képest), a feature maps valójában jobban működik a stílusátvitelhez.

A stílus- és tartalom feature maps-ünknek megfelelő köztes rétegek eléréséhez a megfelelő kimeneteket úgy kapjuk meg, hogy a Keras Functional API segítségével definiáljuk a modellünket a kívánt kimeneti aktivációkkal.

A Functional API segítségével a modell definiálása egyszerűen a bemenet és a kimenet meghatározását jelenti: model = Model(inputs, outputs).

A fenti kódrészletben betöltjük az előre betanított képosztályozó hálózatunkat. Ezután megragadjuk a korábban definiált érdekes rétegeket. Ezután definiálunk egy modellt úgy, hogy a modell bemeneteit egy képre, a kimeneteket pedig a stílus és tartalom rétegek kimeneteire állítjuk be. Más szóval, létrehoztunk egy modellt, amely egy bemeneti képet fogad, és a tartalom és stílus közbenső rétegek kimenetét adja ki!

Meghatározzuk és létrehozzuk a veszteségfüggvényeinket (tartalom és stílus távolságok)

A tartalmi veszteségünk meghatározása valójában nagyon egyszerű. Átadjuk a hálózatnak a kívánt tartalmi képet és az alap bemeneti képünket is. Ez fogja visszaadni a köztes rétegek kimeneteit (a fent definiált rétegekből) a modellünkből. Ezután egyszerűen az euklideszi távolságot vesszük e képek két köztes reprezentációja között.

Formálisabban fogalmazva, a tartalomveszteség egy olyan függvény, amely az x bemeneti képünk és a p tartalmi képünk közötti tartalmi távolságot írja le. Legyen Cₙₙ egy előre betanított mély konvolúciós neurális hálózat. Ebben az esetben is a VGG19-et használjuk. Legyen X bármilyen kép, akkor Cₙₙ(x) az X által táplált hálózat. Legyen Fˡᵢⱼ(x)∈ Cₙₙ(x)és Pˡᵢⱼ(x) ∈ Cₙₙ(x) az x és p bemenetekkel rendelkező hálózat megfelelő köztes jellemzőreprezentációját írja le az l rétegben. Ezután a tartalmi távolságot (veszteséget) formálisan a következőképpen írjuk le:

A visszaterjedést a szokásos módon úgy hajtjuk végre, hogy ezt a tartalmi veszteséget minimalizáljuk. Tehát addig változtatjuk a kezdeti képet, amíg az egy bizonyos (a content_layerben meghatározott) rétegben hasonló választ nem generál, mint az eredeti tartalmi kép.

Ez elég egyszerűen megvalósítható. Ismét az x, a bemeneti képünk és p, a tartalmi képünk által táplált hálózat L rétegének jellemzőtérképeit veszi bemenetként, és a tartalmi távolságot adja vissza.

Stílusveszteség:

A stílusveszteség kiszámítása egy kicsit bonyolultabb, de ugyanazt az elvet követi, ezúttal a hálózatunkat az alap bemeneti képpel és a stílusképpel tápláljuk. Azonban az alap bemeneti kép és a stíluskép nyers köztes kimeneteinek összehasonlítása helyett a két kimenet Gram-mátrixait hasonlítjuk össze.

Matematikailag az alap bemeneti kép, x, és a stíluskép, a, stílusveszteségét e képek stílusreprezentációi (a Gram-mátrixok) közötti távolságként írjuk le. Egy kép stílusreprezentációját a Gˡ Gram-mátrix által adott különböző szűrőválaszok közötti korrelációként írjuk le, ahol Gˡᵢⱼ az l rétegben lévő i és j vektorizált jellemzőtérkép közötti belső szorzat. Láthatjuk, hogy az adott kép jellemzőtérképén generált Gˡᵢⱼ az i és j jellemzőtérképek közötti korrelációt jelenti.

Az alap bemeneti képünk stílusának létrehozásához gradiens ereszkedést végzünk a tartalmi képből, hogy átalakítsuk azt egy olyan képpé, amely megfelel az eredeti kép stílusreprezentációjának. Ezt úgy tesszük, hogy minimalizáljuk a stíluskép és a bemeneti kép feature korrelációs térképe közötti átlagos négyzetes távolságot. Az egyes rétegek hozzájárulását a teljes stílusveszteséghez a

ahol Gˡᵢⱼ és Aˡᵢⱼ az x bemeneti kép és az a stíluskép l rétegben lévő stílusreprezentációja. Nl a jellemzőtérképek számát írja le, amelyek mindegyike Ml=magasság∗szélesség méretű. Így az egyes rétegek teljes stílusvesztesége

ahol az egyes rétegek veszteségének hozzájárulását valamilyen wl faktorral súlyozzuk. Esetünkben minden réteget egyenlően súlyozunk:

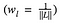
Ez egyszerűen megvalósítható:

Run Gradient Descent

Ha nem ismered a gradiens ereszkedést/visszaterjesztést, vagy szükséged van egy kis felfrissítésre, akkor mindenképpen nézd meg ezt a forrást.

Ez esetben az Adam optimalizálót használjuk a veszteségünk minimalizálása érdekében. Kimeneti képünket iteratív módon úgy frissítjük, hogy az minimalizálja a veszteségünket: nem a hálózatunkhoz tartozó súlyokat frissítjük, hanem a bemeneti képünket képezzük a veszteség minimalizálására. Ehhez tudnunk kell, hogyan számoljuk ki a veszteségünket és a gradiensünket. Megjegyezzük, hogy az L-BFGS optimalizáló, amely, ha ismeri ezt az algoritmust, ajánlott, de ebben a bemutatóban nem használjuk, mivel a bemutató egyik elsődleges motivációja az volt, hogy bemutassuk a legjobb gyakorlatokat a buzgó végrehajtással. Az Adam használatával az autograd/gradiens szalag funkcionalitását egyéni képzési ciklusokkal tudjuk demonstrálni.

Kiszámítjuk a veszteséget és a gradienseket

Meghatározunk egy kis segédfüggvényt, amely betölti a tartalom- és stílusképünket, továbbítja őket a hálózatunkon keresztül, amely aztán kimeneti a modellünk tartalom- és stílusjellemzők reprezentációit.

Itt a tf.GradientTape-t használjuk a gradiens kiszámításához. Ez lehetővé teszi számunkra, hogy a gradiens későbbi kiszámításához kihasználjuk a műveletek követésével elérhető automatikus differenciálást. Rögzíti a műveleteket az előrehaladás során, majd képes kiszámítani a veszteségfüggvényünk gradiensét a bemeneti képünkhöz viszonyítva a visszafelé haladáshoz.

A gradiens kiszámítása egyszerű:

A stílusátviteli folyamat alkalmazása és futtatása

A stílusátvitel tényleges végrehajtásához:

És ennyi!

Futtassuk le a teknősbéka képünkön és Hokusai A nagy hullám Kanagawa előtt című képén:

Nézd meg az iteratív folyamatot az idő múlásával:

Itt van még néhány klassz példa arra, hogy mire képes a neurális stílusátvitel. Nézd meg!

Kipróbáld a saját képeidet!

Mivel foglalkoztunk:

• Elkészítettünk több különböző veszteségfüggvényt, és backpropagationt használtunk a bemeneti képünk átalakítására, hogy minimalizáljuk ezeket a veszteségeket.
• Egy előzetesen betanított modellt töltöttünk be, és annak megtanult jellemzőtérképeit használtuk a képeink tartalmi és stílusbeli reprezentációjának leírására.
• A fő veszteségfüggvényeink elsősorban e különböző reprezentációk távolságának kiszámítása volt.
• Ezt egy saját modellel és eager végrehajtással valósítottuk meg.
• Egyéni modellünket a Functional API segítségével építettük fel.
• A buzgó végrehajtás lehetővé teszi számunkra, hogy dinamikusan dolgozzunk a tenzorokkal, természetes python vezérlési folyamattal.
• A tenzorokat közvetlenül manipuláltuk, ami megkönnyíti a hibakeresést és a tenzorokkal való munkát.

Iteratív módon frissítettük a képünket az optimalizáló frissítési szabályaink alkalmazásával a tf.gradient segítségével. Az optimalizáló minimalizálta az adott veszteségeket a bemeneti képünkhöz képest.