Alai

Michael Fowler,UVa Physics.

A lendületnek van iránya

Amint azt az előző előadáson tárgyaltuk, még mielőtt Newton megfogalmazta volna törvényeit, Descartes, Huygens némi segítségével, felfedezett egy mély dinamikai igazságot: bármilyen ütközésben, vagy valójában bármilyen kölcsönhatásban, a “lendület” – a mozgás mértékegysége – teljes mennyisége mindig ugyanaz maradt. Egy mozgó tárgy impulzusát a tömeg és a sebesség szorzataként határozzák meg, tehát vektor: nagysága és iránya van. Ha súrlódásmentes korcsolyán állsz, és eldobsz egy labdát, akkor hátrafelé mozogsz: a te lendületed nagysága megegyezik a labda lendületével, de ellentétes irányú, így a teljes lendület (a tiéd és a labdáé)nulla marad. A rakéták ugyanígy működnek,nagy sebességgel dobnak ki anyagot. Nem úgy működnek, hogy “nyomják a levegőt”, hanem úgy működnek, hogy nyomják az anyagot, amit kilöknek, ahogyan te is nyomod a bálát, amit dobsz, és az visszalök téged, ami a gyorsulásodat okozza.

Ha még mindig azt gyanítod, hogy a rakéták tényleg a levegő ellen nyomják, ne feledd, hogy ugyanolyan jól működnek az űrben is! Valójában széles körben úgy gondolták, hogy amikor Goddard, egy korai amerikai rakétamérnök (a Goddard Űrrepülési Központot róla nevezték el) az űrben lévő rakétákról beszélt, csak az idejét vesztegette. Egy 1921-es New York Times vezércikkből idézek: “Goddard professzor nem ismeri az akció és a reakció közötti kapcsolatot, és azt, hogy a vákuumnál jobb dologra van szükség a reakcióhoz. Úgy tűnik, hiányzik belőle az az alapismeret, amit a középiskoláinkban naponta oktatnak.” Nyilvánvaló, hogy a New York Times akkori szerkesztői hiányolták az alapvető ismereteket, amelyeket ezen a tanfolyamon oktattak!

Valójában, ahogyan azt már megbeszéltük, a lendület megőrzése az ütközésben Newton törvényeiből következik. Ez azonban egy általánosabb, egyszerűbb fogalom – egyáltalán nem függ a kölcsönhatások részleteitől stb. Ez az egyszerűség nyilvánvalóan vonzotta Einsteint, aki meg volt győződve arról, hogy amikor a dinamikát úgy fogalmazzák újra, hogy az időre és a térre vonatkozó új elképzeléseket is magában foglalja, a lendület megőrzésének továbbra is igaznak kell lennie bármely inerciarendszerben. Ez néhány meglepő következtetéshez vezetett, amint azt látni fogjuk.

A lendület megőrzése a biliárdasztalon

Bemelegítő gyakorlatként tekintsük át a lendület megőrzését két golyó ütközésénél a biliárdasztalon. Húzzunk egy krétavonalat a biliárdasztal közepén, és a golyókat a krétavonalhoz közel, de annak ellentétes oldalaira lőjük mindkét végükről, azonos sebességgel, így a golyók középen csapódnak össze egy ütközéssel, ami a sebességüket egy kis szögben megfordítja. Más szóval, ha kezdetben azt mondjuk, hogy (azonos nagyságú, ellentétes irányú)sebességük párhuzamos volt az x-irányban – a krétavonallal -, akkor az ütközés után az y-irányban is egyenlő és ellentétes kis sebességük lesz (az x-irányú sebességek nagyon kis mértékben csökkentek).

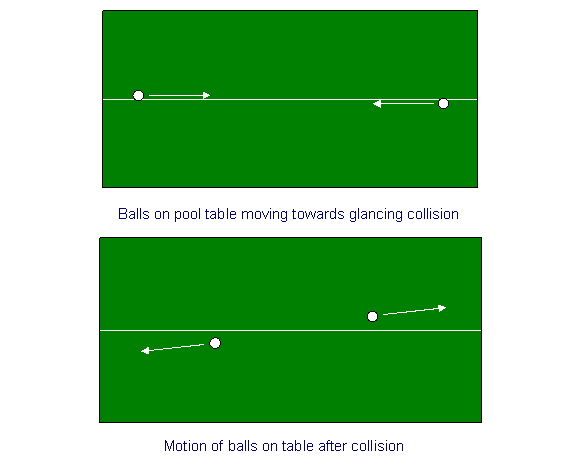
A szimmetrikus űrhajó ütközése

Most ismételjük meg a gyakorlatot nagy léptékben. Tegyük fel, hogy valahol az űrben, távol minden gravitációs mezőtől, kiteszünk egy egymillió mérföld hosszúságú zsinórt. (Ez lehet a két óránk között az időtágulási kísérletben). Ez a húr megfelel a krétavonalnak a biliárdasztalon. Tegyük fel, hogy két egyforma űrhajó közeledik egymáshoz a húrral párhuzamosan, a húr két vége felől egyenlő és ellentétes sebességgel, úgy irányítva őket, hogy amikor középen találkoznak, enyhén ütközzenek. A helyzet szimmetriájából nyilvánvaló, hogy a lendület mindkét irányban megmarad. Különösen az a sebesség, amellyel az egyik űrhajó az ütközés után távolodik a húrtól – az y-sebessége – egyenlő és ellentétes azzal a sebességgel, amellyel a másik űrhajó távolodik a húrtól.

De most tekintsük ezt az ütközést úgy, ahogyan azt valaki az egyik űrhajóban megfigyeli, mondjuk A. Az ütközés előtt látja, hogy a húr nagyon gyorsan mozog az ablaknál, mondjuk néhány méterre tőle. Az ütközés után azt látja, hogy a húr távolodik, mondjuk 15 méter/másodperc sebességgel. Ez azért van, mert az A űrhajó a húrra merőlegesen 15 méter/másodperc sebességet vett fel. Eközben, mivel ez egy teljesen szimmetrikus helyzet, a B űrhajón lévő megfigyelő biztosan arra következtetne, hogy az ő űrhajója is 15 méter/másodperc sebességgel távolodik a húrról.

Mennyire szimmetrikus?

A döntő kérdés az: milyen gyorsan látja az A űrhajót inspiráló megfigyelő, hogy a B űrhajó távolodik a zsinórtól? Tegyük fel, hogy A űrhajóhoz képest B űrhajó 0,6c sebességgel távolodik (x irányban). Először is, emlékezzünk arra, hogy a mozgás irányára merőleges távolságok nem Lorentz-összehúzódnak. Ezért, amikor a B űrhajó megfigyelője azt mondja, hogy egy másodperces intervallumban 15 méterrel távolodott a húrról, az A űrhajóról ezt a mozgást figyelő megfigyelő egyet fog érteni a 15 méterrel – de nem fog egyetérteni az egy másodperccel! Azt fogja mondani, hogy az ő órái lassan járnak, így az ő órái szerint 1,25 másodperc telik el, amíg a nő 15 métert mozog y irányban.

Ebből következik, hogy az időtágulás következtében ez az ütközés az A űrhajóból nézve nem okoz egyenlő és ellentétes sebességet a két űrhajó számára az y irányban. Kezdetben mindkét űrhajó az x-tengellyel párhuzamosan mozgott, az y-irányban nulla momentum volt. Akkor hogyan állíthatjuk, hogy az ütközés után az y irányban nulla a teljes impulzus, ha az azonos űrhajóknak nem egyenlő és ellentétes sebességük van?

Einstein megmenti az impulzusmegmaradást

Einstein annyira biztos volt abban, hogy az impulzusmegmaradásnak mindig fenn kell állnia, hogy egy merész hipotézissel mentette meg: egy tárgy tömegének a sebességétől kell függenie! Valójában a tömegnek a sebességgel éppen úgy kell növekednie, hogy az időtágulásból eredő kisebb y-irányú sebességet kiegyenlítse. Ez azt jelenti, hogy ha egy nyugalomban lévő tárgynak m tömege van, és v sebességgel mozog, akkor a tehetetlensége megfelel a “relativisztikus tömegnek” m rel =m/ 1-( v 2 / c 2 ) .Akkor a lendület

p → = m rel v → =m v → / 1-( v 2 / c 2 ) .

Megjegyezzük, hogy ez a relativisztikus tömegnövekedés hétköznapi sebességnél észrevehetetlenül kis hatás, de ahogy egy tárgy megközelíti a repülési sebességet, a tömeg korlátlanul növekszik!

A tömeg valóban növekszik a sebességgel

Az, hogy az objektumok tömegének a sebességtől kell függenie, nagy árnak tűnik az impulzusmegmaradás megmentéséért! Ez azonban egy olyan jóslat, amelyet nem nehéz kísérletekkel ellenőrizni. Az első megerősítés 1908-ban történt, gyors elektronok eltérítésével egy vákuumcsőben. Valójában az elektronoknak egy régi típusú színTV-csőben körülbelül fél százalékkal nagyobb a tehetetlensége, mint a nyugalmi állapotban lévő elektronoknak, és ezt figyelembe kell venni a mágneses mezők kiszámításakor, amelyekkel a képernyőre irányítják őket.

Sokkal drámaibb, hogy a modern részecskegyorsítókban nagyon erős elektromos tereket használnak az elektronok, protonok és más részecskék gyorsítására. A gyakorlatban kiderült, hogy ezeknek a részecskéknek egyre nagyobb erőre van szükségük a további gyorsításhoz, ahogy a fénysebességet megközelítik. Következésképpen a fénysebesség egy természetes abszolút sebességhatár. A részecskéket olyan sebességre gyorsítják, amelynél a relativisztikus tömegük több ezerszer nagyobb, mint a nyugalomban mért tömegük, amelyet általában “nyugalmi tömegnek” neveznek.

…Vagy mégis?

A fizikusok között folyamatos vita folyik a relativisztikus tömeg fogalmáról. A vita nagyrészt szemantikai: senki sem vonja kétségbe, hogy a v → sebességgel mozgó m nyugalmi tömegű részecske lendületének helyes kifejezése p → = m 1- v 2 / c 2 v → . De különösen a részecskefizikusok, akik közül sokan a részecskék nyugalmi tömegének nagy pontosságú mérésével töltik életüket, nem szívesen írják ezt úgy, hogy p → = m rel v → . Nem tetszik nekik a változó tömeg gondolata. Egyrészt azt a benyomást keltheti, hogy a részecske felgyorsulásával a mérete felduzzad, vagy legalábbis a belső szerkezete valahogy megváltozik. Valójában egy relativisztikus részecske csak Lorentz-összehúzódáson megy keresztül a mozgás iránya mentén, mint bármi más. Gömb alakjából egy ugyanolyan keresztirányú sugárral rendelkező korongszerű alak felé halad.

Hogyan érthető tehát ez a “tömegnövekedés”? Mint mindig, Einsteinnek igaza volt: megjegyezte, hogy az energia minden formája rendelkezik tehetetlenséggel. Maga a mozgási energia is rendelkezik tehetetlenséggel. A “tehetetlenség” pedig a tömeg meghatározó tulajdonsága. A tömeg másik alapvető tulajdonsága, hogy gravitációsan vonz. Ez a mozgási energia is ezt teszi? A válaszhoz tekintsünk egy gázzal töltött gömböt. Ez egy gömbszimmetrikus gravitációs mezőt hoz létre önmagán kívül, amelynek erőssége arányos a teljes tömeggel. Ha most felmelegítjük a gázt, a gázrészecskéknek megnövekedett (relativisztikus) tömege lesz, ami megfelel a megnövekedett mozgási energiájuknak, és a külső gravitációs mező ezzel arányosan megnövekedett. (Senki sem kételkedik ebben.)

Tehát a “relativisztikus tömeg” valóban rendelkezik a tömeg két alapvető tulajdonságával: a tehetetlenséggel és a gravitációs vonzással. (Amint az a következő előadásokon világossá válik, ez a relativisztikus tömeg nem más, mint az összes energia,a nyugalmi tömeget magát most már energiának tekintjük.)

Egy triviálisabb szinten néhány tanár ellenzi arelativisztikus tömeg bevezetését, mert attól tartanak, hogy a diákok azt fogják feltételezni, hogy egy relativisztikusan mozgó részecske mozgási energiája csak 1 2 m v → 2 a relativisztikus tömeg felhasználásával – ez nem így van,amint azt rövidesen látni fogjuk.

Lábjegyzet: Mindenki számára, aki valamikor továbbmegy egy matematikailag kifinomultabb kezelésre, hozzá kell tenni, hogy a nyugalmi tömeg fontos szerepet játszik, mint invariáns az egyik vonatkoztatási rendszerből a másikba való átlépéskor, de az itt használt “relativisztikus tömeg” valójában csak a részecske négydimenziós energia-momentumvektorának első összetevője (az energia), és így nem invariáns.

Kinetikus energia és tömeg nagyon gyors részecskék esetén

Gondoljunk egy ilyen, a fénysebességhez közel haladó részecske kinetikus energiájára. Emlékezzünk vissza, hogy egy korábbi előadáson azt találtuk, hogy egy közönséges nemrelativisztikus (azaz lassan mozgó) m tömeg mozgási energiája 1 2 m v 2 . Ezt úgy értük el, hogy megnéztük, mekkora munkát kell végeznünk ahhoz, hogy egy bizonyos magasságon át felemeljük: W tömegével megegyező erőt kell kifejtenünk ahhoz, hogy h magasságon át felemeljük, a teljes elvégzett munka vagy ráfordított energia pedig az erő x távolság Wh. Amikor visszaesett lefelé, a gravitációs erő, W, pontosan ugyanannyi munkát, Wh-t végzett a zuhanó tárgyon, de ezúttal a munka a tárgy gyorsulásába ment át, hogy mozgási energiát adjon neki. Mivel tudjuk, hogy a zuhanó tárgyak milyen gyorsan veszik fel a sebességet, arra tudtunk következtetni, hogy a mozgási energia 1 2 m v 2 volt. (A részleteket lásd az előző előadásban.)

Még általánosabban, felgyorsíthattuk volna a tömeget bármilyen konstans F erővel, és megtalálhattuk volna az erő által végzett munkát (erő xtávolság), hogy álló helyzetből v sebességre gyorsuljon. A tömeg mozgási energiája, E= 1 2 m v 2 , pontosan megegyezik az erő által a tömegnek a sebesség eléréséhez végzett munkával. (Hasonlóképpen kimutatható, hogy ha mondjuk egy már u sebességgel mozgó részecskére erőt fejtünk ki, és azt v sebességre gyorsítjuk, a szükséges munka 1 2 m v 2 – 1 2 m u 2 ).

Érdekes megpróbálni megismételni a feladatot a fénysebességhez nagyon közel mozgó részecskékre, mint például az előző bekezdésben említett gyorsítókban lévő részecskékre. Newton második törvénye

erő = lendületváltozás sebessége

formában még mindig igaz, de a fénysebességhez közel a sebesség elhanyagolható mértékben változik, ahogy az erő tovább hat – ehelyett a tömeg növekszik! Ezért kiváló közelítéssel azt írhatjuk,

erő = (tömegváltozás sebessége) x c

ahol a szokásos módon c a fénysebesség. Hogy pontosabbak legyünk, tegyük fel, hogy van egy állandó F erő, amely egy részecskét nyom egy részecskét. Egy adott pillanatban a részecske tömege M, sebessége pedig rendkívül közel van c-hez. Egy másodperccel később, mivel az erő tovább hat a részecskére, és így Newton második törvénye alapján növeli annak lendületét, a részecske tömege mondjuk M+m lesz, ahol m a tömegnövekedés az erő által végzett munka eredményeként.

Mennyivel nő a részecske mozgási energiája E ebben az egy másodperces periódusban? A fentebb áttekintett nem-relativisztikus eset pontos analógiájára, ez csak az erő által végzett munka ebben az időszakban. Most, mivel a részecske tömege egy másodperc alatt m-rel változik, m a tömegváltozás sebessége is. Ezért Newton második törvényéből

erő = (tömegváltozás sebessége) x c,

felírhatjuk

erő =mc.

A mozgási energia E növekedése az egy másodperces időtartam alatt csak az erő által végzett munka,

E= erő x távolság.

Mivel a részecske lényegében fénysebességgel mozog, az erő által az egy másodperces időtartam alatt megtett távolság csak c méter, c=3× 10 8 .

Az erő által ebben a másodpercben kifejtett teljes munka tehát: erő x távolság =mc×c=m c 2 .

Az összefüggés a relativisztikus részecske tömegnövekedése és mozgási energiájának növekedése között tehát a következő:

E=m c 2 .

Kinetikus energia és tömeg lassú részecskékre

Emlékezzünk vissza, hogy ahhoz, hogy Newton törvényei minden inerciarendszerben igazak legyenek, feltételeznünk kellett, hogy a tömeg a sebességgel 1/ 1-( v 2 / c 2 ) tényezővel nő. Ez azt jelenti, hogy még egy lassan mozgó tárgynak is van egy kis tömegnövekedése, amikor mozog!

Hogyan viszonyul ez az apró növekedés a mozgási energiához? Tekintsünk egy M tömeget, amely v sebességgel mozog, ami sokkal kisebb, mint a fénysebesség. A mozgási energiája E= 1 2 M v 2 , ahogy fentebb tárgyaltuk. Tömege M/ 1-( v 2 / c 2 ) , amit felírhatunk M+m-nek. Mekkora m ?

Mivel olyan sebességekről beszélünk, amelyeket ismerünk, mint például egy sugárhajtású repülőgép, ahol v/c, nagyon kicsi, használhatunk néhány egyszerű matematikai trükköt a dolgok megkönnyítésére.

Az első egy jó közelítés az 1-x négyzetgyökére, amikor x sokkal kisebb, mint egy:

1-x ≅1- 1 2 x esetén x≪1.

Ezt könnyen ellenőrizheted a számológéppel: próbáld ki x= 1 100 , azt találod, hogy 99 100 =0,994987… ami rendkívül közel van 1- 1 2 1 100 =0,995 !

A következő közelítés

1 1-x ≅1+x for x≪1.

Ezt is könnyű ellenőrizni: vegyük ismét x= 1 100 : 1 1-x = 1 99 100 = 100 99 =1,01010… ,és 1+x= 101 100 =1,01.

Ezeket a közelítéseket x=v/c-vel használva 1-( v 2 / c 2 ) 1- 1 2 ( v 2 / c 2 ) -ként közelíthetjük ,majd 1/( 1- 1 2 ( v 2 / c 2 ) ) -ként 1+ 1 2 ( v 2 / c 2 ) -ként.

Ez azt jelenti, hogy a teljes tömeg v sebességnél

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ),

és ezt M+m-nek írva azt látjuk, hogy a tömegnövekedés m egyenlő 1 2 M v 2 / c 2 .

Ez azt jelenti, hogy – ismét – az m tömegnövekedés az E mozgási energiával az E=m c 2 -vel függ össze.

Tény, hogy egy kis számítással nem nehéz megmutatni, hogy a sebesség teljes tartományában, a nullától a fénysebességhez tetszőlegesen közeli sebességig, egy mozgó részecske tömegnövekedése a kinetikus energiájához képest E=m c 2 . Hogy megértsük, miért nem vesszük ezt észre a mindennapi életben, próbáljunk ki egy példát, például egy 100 tonnás repülőgépet, amely 2000 mérföld/órás sebességgel mozog. A 100 tonna 100 000 kilogramm, a 2000 mérföld/óra pedig körülbelül 1000 méter másodpercenként. Ez 1 2 M v 2 ½ × 1011 joule kinetikus energiát jelent, de a repülőgép megfelelő tömegváltozása a c 2 -szeresével, 9× 10 16, ami körülbelül fél milligrammnyi tényleges tömegnövekedést jelent, amit nem túl könnyű észrevenni!

E = mc2

A fentiekben láttuk, hogy amikor egy erő munkát végez egy test gyorsításával, hogy mozgási energiát adjon neki, a test tömege az erő által végzett teljes munkával, az átadott E energiával egyenlő mértékben nő, osztva c 2 -vel. Mi a helyzet akkor, amikor egy erő olyan munkát végez egy testen, amely nem gyorsítja fel azt, így a mozgási energia nem növekszik? Mi van például, ha csak felemelek valamit egyenletes sebességgel, potenciális energiát adva neki? Kiderül, hogy ebben az esetben is van egy tömegnövekedés, amelyet az E=m c 2 ad meg, természetesen mérhetetlenül kicsi a mindennapi tárgyak esetében.

Ez azonban mérhető és fontos hatás az atommagfizikában. Például a héliumatomnak van egy olyan atommagja, amely két protonból és két neutronból áll, amelyeket nagyon szorosan összeköt az erős nukleáris vonzóerő. Ha elegendő külső erőt alkalmazunk, ez két “nehéz hidrogén” atommagra választható szét, amelyek mindegyike egy protonból és egy neutronból áll. A szétválasztáshoz sok külső energiát kell felhasználni, és kiderül, hogy a két nehézhidrogén atommag össztömege mérhetően (körülbelül fél százalékkal) nehezebb, mint az eredeti héliummagé. Ez az extratömeg, megszorozva c 2 -vel, éppen megegyezik a héliummag kettéhasadásához szükséges energiával. Még fontosabb, hogy ez az energia visszanyerhető, ha hagyjuk, hogy a két nehéz hidrogénmag összeütközzön és újra egy héliummagot alkotva egyesüljön. (Mindkettő elektromosan pozitív töltésű, ezért taszítják egymást, és elég gyorsan kell összeérniük, hogy legyőzzék ezt a taszítást, és olyan közel kerüljenek egymáshoz, ahol a sokkal erősebb magvonzás működésbe lép.) Ez a hidrogénbomba és a Nap alapvető energiaforrása.

Kiderül, hogy az energia minden formája, a mozgási és a potenciális energia különböző fajtái, az E=m c 2 által meghatározott tömeggel rendelkeznek. A nukleáris reakciók esetében a tömegváltozás tipikusan a teljes tömeg egy ezrelékének nagyságrendje, és könnyen mérhető. Kémiai reakcióknál a változás a teljes tömeg milliárdod része, és jelenleg nem mérhető.

előző index