ロバスト統計学の次の定義は、P. J. Huberの著書「ロバスト統計学」から来ています。
…どんな統計的手法も以下の望ましい特徴を持つべきである:
- 仮定したモデルで適度に良い(最適またはほぼ最適)効率を持つべきである。
- モデルの仮定からの小さな逸脱は性能をわずかに損なうだけという意味で、頑健であるべきだ。 …
- モデルからの多少大きな逸脱はカタストロフィーを引き起こしてはならない。
古典統計学はHuberのポイントの最初のものに焦点を当て、ある基準の下で最適である方法を生成します。 この記事では、Huberの2番目と3番目のポイントを説明するために使用される正規の例を見てみましょう。
Huberの3番目のポイントは、一般的に標本平均(平均)と標本中央値(中央値)によって説明されます。 標本中央値が無限大になることなく、標本のほぼ半分のデータを∞に設定することができます。 一方、標本平均は、どの標本値も無限大になると無限大になります。 モデルからの大きな逸脱、すなわち少数の外れ値は、標本平均の破局を引き起こすが、標本中央値の破局は引き起こさない。 すなわち、データは未知の平均と分散1を持つ正規分布からのデータで、μが未知であるnormal(μ, 1)である。 μを推定する最も効率的な方法は標本平均、つまりデータの平均をとることです。
しかし、ここでデータの分布が正確に正規分布(μ, 1)ではなく、標準正規分布と異なる分散の正規分布の混合であると仮定します。 この分布を「汚染正規分布」といい、δは汚染の度合いを表します。 汚染された正規モデルを使う理由は、見た目には正規分布に見えるかもしれない非正規分布だからです。
標本平均と標本中央値のどちらかを使って母平均μを推定することができます。 もしデータが混合ではなく、厳密に正規分布であれば、標本平均が最も効率的なμの推定量になります。 その場合、標本中央値を用いると標準誤差は約25%大きくなります。 しかし、もしデータが混合物から得られたものであれば、δとσの大きさによっては標本中央値の方が効率的な場合があります。 ここに、δ=0の時の標本中央値と標本平均値のARE(漸近的相対効率)をσの関数としてプロットしておきます。
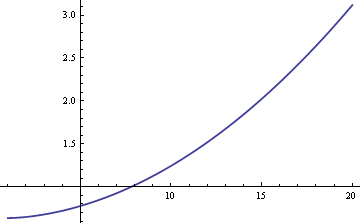
このプロットは、σが8より大きい場合、標本中央値が標本平均値より効率的であることを示している。
ここで、σを10に固定し、δを0から1の間で変化させたAREのプロットを示します。
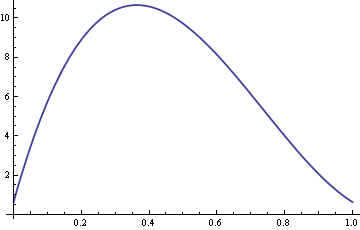
したがって、δを0付近とした場合、中央値対平均値は0.1付近となります。
この例でのAREの一般式は2((1 + δ(σ2 – 1)(1 – δ + δ/σ)2)/π) です。
データが汚染されていない、または汚染が非常に少ない正規であると確信している場合、サンプル平均は最も効率の良い推定量と言えます。 しかし,有意な汚染がある場合にロバストモデルでより良い結果が得られることを知ることと引き換えに,多少の効率をあきらめるリスクを冒すことは価値があるかもしれません。
ここで、汚染された正規の例と関連した難問があります。 normal(μ, 1)データに対する最も効率的な推定量は標本平均です。 そしてnormal(μ, σ2)のデータに対する最も効率的な推定量も標本平均をとることである。
重要なのは、あるサンプルがnormal(μ, 1)分布から来たのか、normal(μ, σ2)分布から来たのかわからないということです。 もし分かっていれば、サンプルを分離し、別々に平均化し、サンプルを集計平均にまとめることができます。一方の平均に1-δをかけ、もう一方にδをかけて、足せばいいのです。 しかし、混合物のどの成分がどの試料につながるかが分からないので、試料を適切に計量することができません。 (おそらくδもわからないと思いますが、それは別問題です。)
標本平均や標本中央値を使う以外の選択肢もあります。 たとえば、切り捨て平均では、最大値と最小値のいくつかを捨て、それ以外を平均化します。 (スポーツがこの方法で、審判からの選手の最高点と最低点を除外することがあります)。 両端のデータを捨てれば捨てるほど、切り捨て平均は標本中央値のような働きをします。 捨てるデータが少ないほど、標本平均のような働きをします。
関連記事 Student-t 分布の中央値と平均値の効率性
データ サイエンスに関する毎日のヒントについては、Twitter で @DataSciFact をフォローしてください。