伝送路の導体は、その間にコンデンサを構成しています。 送電線の導体はコンデンサの平行板として働き、その間の空気はちょうど誘電体媒体のようなものです。 線路の静電容量は、導体間の誘導電流を生じさせます。 それは導体の長さに依存します。
ラインの静電容量は、伝送線路の長さに比例しています。 その影響は,短い(長さが80km以下)低電圧送電線の性能には無視できるほどです。 高電圧で長い線路の場合、最も重要なパラメータの1つとみなされる。
2線式線路の静電容量
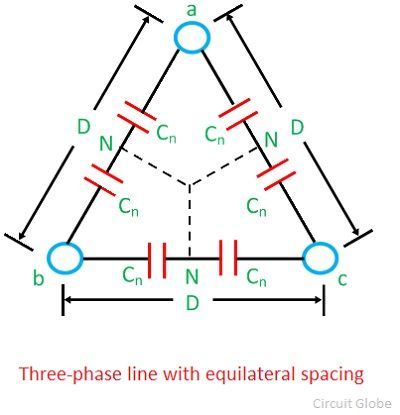
伝送線路の静電容量はコンダクタンスとともに、シャントアドミタンスを形成している。 伝送線路のコンダクタンスは、導体表面での漏れによるものです。 半径rの2本の導体a、bからなる線路を考える。 導体間の距離をDとすると、下図のようになります。-
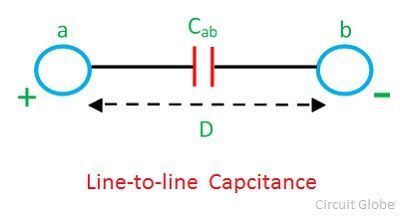 導体 a と b の間の電位差は
導体 a と b の間の電位差は
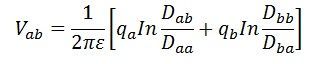 ここで、qa – 導体 a の電荷
ここで、qa – 導体 a の電荷
qb – 導体 b の電荷
Vab – 導体 a と b の電位差
ε- 絶対誘電率
![]() ですから、以下のようになります。
ですから、以下のようになります。
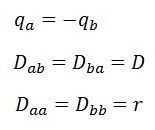 これらの値を電圧の式に代入すると
これらの値を電圧の式に代入すると
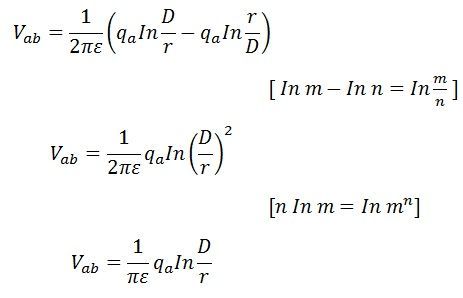 導体間の静電容量は
導体間の静電容量は
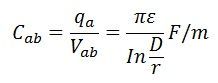 線間容量と呼ばれます。
線間容量と呼ばれます。
二つの導体a、bが反対に帯電しており、それらの間の電位差がゼロであれば、各導体の電位は1/2 Vabで与えられる。
 各導体とゼロ電位の点n間の静電容量は
各導体とゼロ電位の点n間の静電容量は
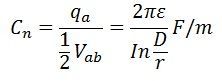 Capacitance Cnは中立または接地への容量
Capacitance Cnは中立または接地への容量
Capacitance Cabは二つの同じ容量a、bを直列したもので、静電容量と呼ばれる。 したがって、中性点までの静電容量は、導体間の静電容量の2倍、すなわち
![]() 絶対誘電率εは
絶対誘電率εは
![]() ここでεoは自由空間の誘電率、εrは媒体の相対誘電率で与えられる。
ここでεoは自由空間の誘電率、εrは媒体の相対誘電率で与えられる。
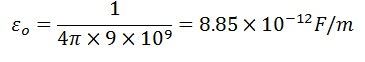 空気の場合
空気の場合
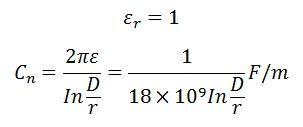 一導体と中性線の間の静電容量リアクタンス
一導体と中性線の間の静電容量リアクタンス
対称三相線
以下に示す対称三相線に平衡系の電圧をかける
 等角間隔の三相線の位相図が以下に示す通りである。
等角間隔の三相線の位相図が以下に示す通りである。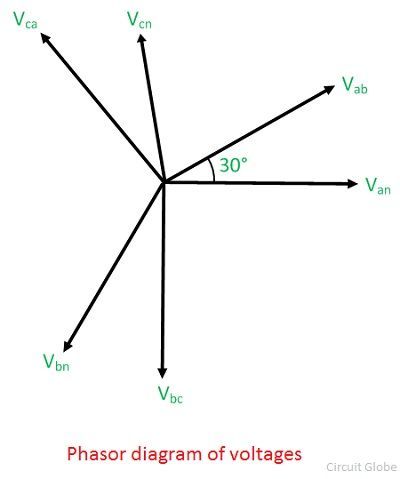 中性点に対する導体aの電圧を基準位相とすると
中性点に対する導体aの電圧を基準位相とすると
![]() 導体aとbの電位差は
導体aとbの電位差は
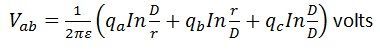
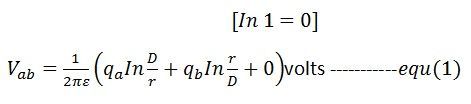 同様に導体aとcの電位差は
同様に導体aとcの電位差は
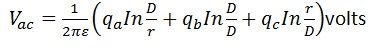
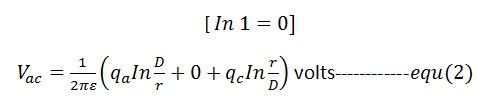 (1) と (2) 式を加えて、(1)式が得られます。 が得られる
(1) と (2) 式を加えて、(1)式が得られます。 が得られる
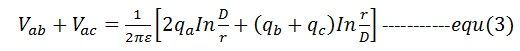 も。
も。
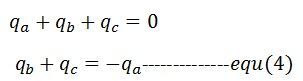 (3)式と(4)式より
(3)式と(4)式より
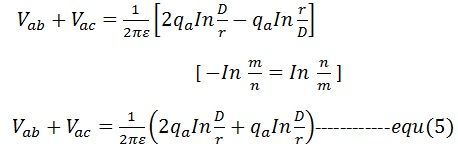
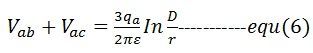
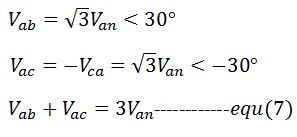 式より
式より
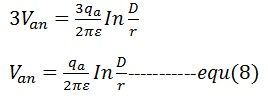 線対中性点容量
線対中性点容量
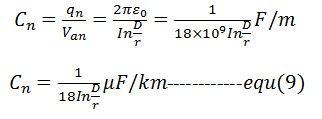 対称型三相線は二線式と同じ静電容量とすることができる。
対称型三相線は二線式と同じ静電容量とすることができる。