Alai

Michael Fowler（UVA物理学専攻）。

運動量には方向性がある

前回の講義で述べたように、ニュートンが法則を打ち立てる以前から、デカルトはホイヘンスの助けを借りて、深い力学的真実を発見していました：いかなる衝突、あるいは実際にはいかなる種類の相互作用においても、運動の尺度である「運動量」の合計量は常に同じであること。 移動する物体の運動量は、質量と速度の積として定義され、ベクトルであるため、大きさと方向があります。 摩擦のないスケートの上に立っていて、ボールを投げると、あなたは後方に移動します。あなたの運動量はボールの運動量と同じですが、方向が反対なので、あなたの運動量とボールの運動量の合計はゼロのままです。 ロケットも同じように、高速で物質を投げ出すことによって機能します。 ロケットは「空気を押し出す」のではなく、「押し出す」ことによって機能します。ちょうど、あなたが投げているバリケードを押し出すと、それがあなたを押し戻し、あなたの加速を引き起こすように。

それでもなお、ロケットが空気を押し返すと思うのなら、宇宙でも同じように機能することを思い出してください! 実際、アメリカの初期のロケット研究者であるゴダード（ゴダード宇宙飛行センターは彼の名前に由来する）が宇宙でのロケットについて話したとき、彼は時間の無駄だったと広く信じられていました。 1921年に書かれたニューヨークタイムズの社説から引用すると、次のようになる。 「ゴダード教授は作用と反作用の関係を知らないし、反応するためには真空よりもよいものを持たなければならないことも知らない。 彼は、我々の高校で毎日配られる基本的な知識に欠けているようだ”。 明らかに、当時のニューヨークタイムズの論説委員は、このコースで杓子定規に教えられている基本的な知識を裏付けていたのだ!

実際、私たちが議論したように、衝突における運動量の保存はニュートンの法則から導かれます。 しかし、これはより一般的で単純な概念であり、相互作用の詳細などには全く依存しません。 この単純さがアインシュタインに気に入られ、力学が時間と空間についての新しい考えを含むように定式化されたとき、運動量保存はどの慣性フレームでも成立するはずだと確信したのである。 このことは、後述するように、彼をいくつかの驚くべき結論に導いた。

ビリヤード台での運動量保存

ウォーミングアップとして、ビリヤード台での2つのボールの衝突に対する運動量保存を考えてみよう。 ビリヤード台の中央にチョーク線を引き、その両端からチョーク線に近いが反対側の球を同じ速度で発射すると、中央でぶつかり、その速度が小さな角度で回転することになる。 つまり、当初、両者の（同じ大きさで反対方向の）速度がx方向、つまりチョークラインに平行だったとすると、衝突後はy方向にも同じ大きさで反対方向の小さな速度が発生します（x方向の速度はごくわずかに減少します）。

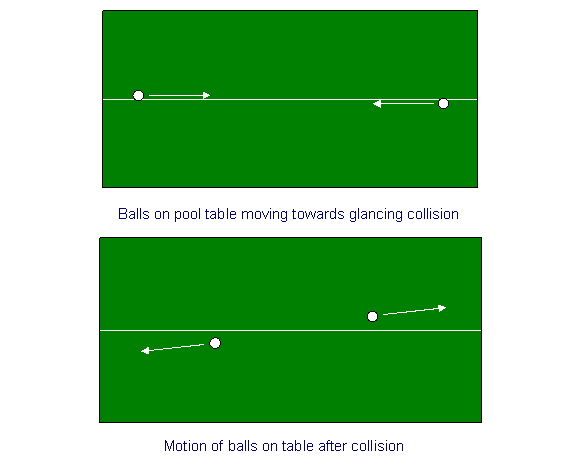
対称な宇宙船の衝突

さて、この演習を大きなスケールで行ってみましょう。 重力場から遠く離れた宇宙のどこかに、100万マイルの長さの糸を張ったとしよう。 (これは、時間拡張の実験では、2つの時計の間でもよい）。 このひもは、ビリヤード台のチョークラインに相当する。 今、2つの同じ宇宙船が、紐の両端から紐に平行に等しく反対の速度で接近し、中央で出会うときにわずかにかすめるように衝突するように狙ったとする。 この場合、運動量は両方向に保存されることは対称性から明らかである。 特に、衝突後に一方の宇宙船がひもから離れる速度（y-速度）は、もう一方の宇宙船がひもから離れる速度と等しく、反対である。

しかし、この衝突を一方の宇宙船（Aとする）に乗っている人が観察した場合を考えてみよう。衝突の前、彼は窓際、例えば数メートル先で非常に速く動くひもを見た。 衝突の後、彼は、ひもは、例えば、毎秒15メートルの速さで遠ざかっているのが見えます。 これは、宇宙船Aはひもに垂直な方向の速度を秒速15mにしたためである。 一方、これは完全に対称的な状況なので、宇宙船Bの観測者は、自分の宇宙船も同様に秒速15mでひもから遠ざかっていると推論することになるのです。

どのくらい対称なのか？

ここで重要なのは、宇宙船Aを見た観測者が、宇宙船Bがどの程度の速さでひもから離れると見るか、ということです。 仮に宇宙船Aに対して宇宙船Bが0.6cで（x方向に）離れているとしましょう。 まず、進行方向に垂直な距離はローレンツ収縮しないことを思い出してください。 したがって、宇宙船Bの観測者が1秒間にひもから15メートル離れたと言った場合、宇宙船Aからこの動きを見ている観測者は15メートルについては同意するが、1秒については同意しない！宇宙船Bの観測者は1秒間にひもから15メートル離れたと言った場合、宇宙船Aの観測者は15メートルについては同意するが、1秒については同意しない！宇宙船Bの観測者は、1秒間にひもから15メートル離れたと言った。 彼は、彼女の時計はゆっくり動いているので、彼の時計で測ると、彼女がY方向に15m移動する間に1.25秒経過していることになると言うでしょう。

このことから、宇宙船Aから見たこの衝突は、時間拡張の結果、2つの宇宙船のy方向の速度が等しくなく、逆になっていることがわかります。 当初、両宇宙船はx軸に平行に移動しており、y方向にはゼロ運動量が存在する。 では、同じ宇宙船が等速度でも逆速度でもないのに、衝突後のy方向の運動量がゼロであると言えるのでしょうか？

アインシュタインによる運動量保存の救済

アインシュタインは運動量保存が常に成り立つと確信していたので、それを大胆な仮説で救済しました：物体の質量はその速度に依存するはずだ！ということです。 つまり、物体の質量はその速度に依存するはずだ！実際、質量は時間の拡張によるY方向の速度低下を打ち消すように、速度とともに増加するはずである。 つまり、静止している物体に質量mがあるとすると、速度vで動くときには「相対論的質量」m rel =m/ 1-( v 2 / c 2 ) に相当する慣性を持つことになり、運動量は

p → = m rel v → =m v → / 1-( v 2 / c 2 ) となるのです。

この相対論的な質量増加は、通常の速度では検出できないほど小さな効果であるが、物体が飛行速度に近づくと、質量は際限なく増加することに注意されたい。

質量は本当に速度によって増加する

物体の質量がこのように速度に依存すると決めることは、運動量保存を救うための重い代償のように思えます! しかし、この予測は実験によって確認することが難しいものではありません。 最初の確認は1908年、真空管内の高速電子を偏向させることによって行われた。 実際、旧式のカラーテレビ管内の電子は静止している電子よりも約半分以上の慣性を持っており、このことは電子をスクリーンに導くための磁場の計算において考慮されなければならない。

もっと劇的なのは、現代の粒子加速器では、電子、陽子、その他の粒子を加速するために非常に強力な電場が使用されていることである。 そのため、光の速度に近づくにつれて、これらの粒子をさらに加速するために、より大きな力を必要とすることが実際に判明しています。 その結果、光速は自然な絶対速度限界となる。 粒子は、相対論的質量が通常「静止質量」と呼ばれる静止状態で測定された質量よりも数千倍大きくなる速度まで加速される。

…Or Does It?

実は、この相対論的質量という概念について、物理学者の間で議論が続いている。 静止質量 m を持つ粒子が速度 v → で動くときの運動量の正しい式が p → = m 1- v 2 / c 2 v → であることに誰も疑いはないのである。 しかし、特に素粒子物理学者の多くは、粒子の静止質量を高精度で測定することに生涯を費やしているので、これをp → = m rel v → と書くことに抵抗があるようです。 彼らは質量が変化することを好まないのです。 ひとつには、速度が上がると粒子が膨らんでしまう、あるいは少なくともその内部構造が変化してしまうという印象を与える可能性があるからだ。 実際には、相対論的な粒子は、他のものと同様に、運動方向に沿ってローレンツ収縮を受けるだけである。 球形から、同じ横半径を持つ円盤状になるのである。 例によってアインシュタインは、あらゆるエネルギーが慣性を持つことを指摘したのである。 運動エネルギーそのものが慣性を持っているのです。 この「慣性」は、質量の定義的な性質です。 質量のもう一つの基本的な性質は、重力によって引き合うことである。 この運動エネルギーは、そのような性質を持っているのでしょうか？ その答えを知るために、気体で満たされた球体を考えてみましょう。 この球体は、球対称の重力場を外部に発生させ、その強さは全質量に比例する。 このとき、気体を加熱すると、気体粒子の質量は相対論的に増加し、運動エネルギーも増加し、外部の重力場もそれに比例して増加します。 (このことは誰も疑わない）

だから「相対論的質量」は確かに質量としての二つの基本的な性質、すなわち慣性と引力をもっているのである。 (次の講義で明らかになるように、この相対論的質量は全エネルギーに他ならず、静止質量そのものがエネルギーと見なされているのである。

脚注：いつかもっと数学的に洗練された研究に進む人のために、静止質量はある参照枠から別の参照枠に移るときの不変量として重要な役割を果たすが、ここで使われている「相対論的質量」は実際には粒子の4次元エネルギー運動量ベクトルの第1成分（エネルギー）に過ぎないので、不変量ではないと補足しておく必要がある。

超高速粒子の運動エネルギーと質量

光速に近い速度の粒子の運動エネルギーについて考えてみましょう。 以前の講義で、普通の非相対論的な（つまりゆっくり動く）質量mの運動エネルギーが1 2 m v 2 であることを発見したことを思い出してください。 その方法は、ある高さまで持ち上げるのに、どれだけの仕事をしなければならないかを考えることであった。重さWに等しい力をかけて、高さhまで持ち上げなければならなかった。 物体が下に落ちるとき、重力の力Wは落下する物体に全く同じ量の仕事Whをしますが、今度はその仕事が物体を加速し、運動エネルギーを与えるために使われます。 落下する物体の速度が分かるので、運動エネルギーは 1 2 m v 2 であると結論付けることができました。 (詳細は前回の講義を参照)

より一般的には、任意の定数力Fで質量を加速し、立っている状態から速度vにするために力によってなされた仕事(力×距離)を求めればよかったのです。 質量の運動エネルギーE= 1 2 m v 2 は、質量をその速度にするために力によってなされた仕事と正確に等しくなります。 (同様の方法で、例えば既に速度uで動いている物体に力を加えて速度vまで加速する場合、必要な仕事は1 2 m v 2 – 1 2 m u 2 であることが示される)。

前項の加速器内の粒子のように、光速に非常に近い速度で動く粒子について、この演習を繰り返してみるのも面白いでしょう。 ニュートンの第二法則

Force = rate of change of momentum

は正しいのですが、光速に近いところでは、力が働き続けても速度はほとんど変化せず、代わりに質量が増加するのです！この法則は、光速に近いところでは、力が働き続けても速度はほとんど変化せず、代わりに質量が増加するのです。 したがって、近似的に

力＝（質量変化率）×c

ここでcは例によって光速である、と書くことができます。 もう少し具体的に説明すると、ある粒子を押す一定の力Fがあるとする。 ある瞬間、粒子は質量Mを持ち、速度はcに極めて近い。1秒後、力は粒子に働き続けているので、ニュートンの第二法則から運動量が増加し、粒子は質量M+mを持つことになる。

その1秒間に粒子の運動エネルギーEが増加するのは何であろうか。 上に述べた非相対論的な場合との正確な類推により、それはその間に強制された仕事だけである。 さて、粒子の質量は1秒間にmだけ変化するので、mは質量の変化率でもあります。 したがって、ニュートンの第二法則から、

力＝（質量変化率）×c という形で、

力＝mc と書くことができる。

1秒間の運動エネルギーの増加Eは、ちょうど力の働きで、

E=力×距離です。

粒子は基本的に飛行速度で動いているので、1秒間に力が働く距離はわずかcメートル、c=3×10 8です。

ですから、その1秒間に力がする総仕事は、力×距離＝mc×c＝m c 2 となります。

したがって、Therelativistic粒子の質量の増加と運動エネルギーの増加の関係は、次のようになります。

E=m c 2 .

低速粒子の運動エネルギーと質量

すべての慣性フレームでニュートンの法則を成立させるには、速度に伴って質量が 1/ 1-( v 2 / c 2 ) だけ増加すると仮定しなければならなかったことを思い出してください。 このことは、ゆっくり動いている物体でも、動くと質量がわずかに増加することを意味しているのです

その微小な増加分は運動エネルギーとどう関係するのだろうか。 光速よりはるかに小さい速度vで動く質量Mを考えてみましょう。 その運動エネルギーE= 1 2 M v 2 は、前述したとおりです。 その質量はM/ 1-( v 2 / c 2 ) であり、M+mと書くことができる。 mとは何でしょうか？

ジェット機のようにv/cが小さい身近な速度の話なので、簡単な数学的トリックを使って簡単にすることができます。

最初のものは、x が 1 よりずっと小さいとき、1-x の平方根の良い近似です：

1-x ≅1- 1 2 x for x≪1.

これを電卓で簡単に確認できます。x= 1 100 とすると、99 100 =0.994987… これは 1- 1 2 1 100 =0.995 に極めて近い！

次の近似は

1 1-x ≅1+x for x≪1…

これも確認は簡単で、再びx= 1 100 : 1 1-x = 1 99 100 = 100 99 =1.01010… , 1+x= 101 100 =1.01 とします。

これらの近似をx=v/cとすると、1-( v 2 / c 2 ) を 1- 1 2 ( v 2 / c 2 ) と近似し、1/( 1- 1 2 ( v 2 / c 2 ) ) を 1+ 1 2 ( v 2 / c 2 ) と近似することができる。

これは、速度vにおける全質量

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ),

これをM+mと書くと、質量増加mは1 2 M v 2 / c 2となることがわかります。

このことから、やはり質量増加量mは運動エネルギーEとE=m c 2で結ばれていることがわかります。

実際、微積分を使えば、ゼロから光速に近い速度までの全範囲で、移動する粒子はその運動エネルギーに関連してE=m c 2による質量増加を経験することを示すのは難しいことではありません。 日常生活でこのことに気づかない理由を理解するために、例えば、100トンの重さのジェット機が時速2,000マイルで移動しているとします。 100トンは10万キログラム、時速2,000マイルは1秒間に約1,000メートルです。 運動エネルギー1 2 M v 2 は1/2 ×1011ジュールですが、それに対応する飛行機の質量変化は係数c 2 、9×10 16で、実際の質量増加は約半分ミリグラムとなり、検出はあまり簡単ではありません

E = mc2

力が物体を加速して運動エネルギーを与えるとき、物体の質量は、力によって与えられた仕事の合計、伝達エネルギーEをc 2で割った量だけ増えることを上で見てきた。 では、ある力が物体に働きかけても、その物体が加速されないので、運動エネルギーが増加しない場合はどうでしょうか？ 例えば、あるものを一定の速度で持ち上げ、位置エネルギーを与えたとしたらどうでしょう？ この場合も、E=m c 2で与えられる質量の増加があることがわかりますが、もちろん日常的な物体では測定不能なほど小さいものです。

しかし、これは原子核物理学では測定可能で重要な効果である。 例えば、ヘリウム原子の原子核は、2個の陽子と2個の中性子が強い核引力でぴったりと結合しています。 しかし、十分な外力を加えれば、陽子1個と中性子1個を持つ2つの「重水素」原子核に分離することができる。 この分離には多くの外部エネルギーが必要で、2つの重水素原子核の合計質量は、元のヘリウム原子核よりもわずかに（約半分）重くなることが判明した。 この質量にc2をかけると、ちょうどヘリウム原子核を2つに分けるのに必要なエネルギーと同じになります。 さらに重要なことは、このエネルギーは、2つの重い水素原子核を衝突させて結合させ、再びヘリウム原子核を形成させることで回収できることである。 (両者はプラスに帯電しているので、互いに反発し合い、この反発に打ち勝って、より強い核の引力が働くところまで接近するには、かなり速く接近する必要がある)。 これが水爆や太陽の基本的な動力源です。

すべてのエネルギー、運動エネルギーとさまざまな種類の位置エネルギーは、E=m c 2 で与えられる関連する質量を持っていることがわかりました。 核反応では、質量変化は通常、全質量の1000分の1のオーダーであり、容易に測定可能である。 化学反応では、質量変化は全質量の10億分の1のオーダーであり、現在では測定不可能である。