群の掛け算
ここで、2つの対称操作を順番に適用するとどうなるかを調べてみましょう。 例として、点群「C_{3v}」に属する分子「NH_3」を考えてみましょう。 このとき、(C_3)回転の後に(C_3)反射を行うとどうなるか考えてみましょう。 この複合演算を \(\sigma_v**)\(C_3**) と書きます(対称演算は、量子力学の演算子のように、その右隣のものを操作するため、表記を右から左へ逆算して、正しい順番で演算を行う必要があります)。
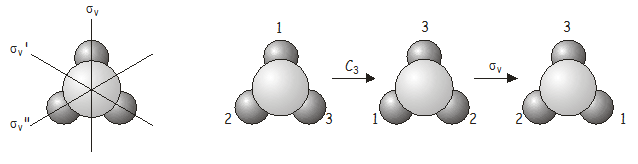
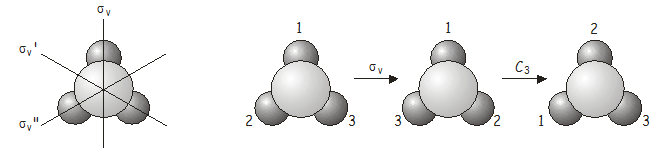
Acomplete operation \(C_3)\(\sigma_v) is equivalent to another operation of the point group, this time (\sigma_v’\).
この例からわかる重要な点は2つあります。
ある点群の中で2つの対称操作を順番に適用した場合の効果を群乗算表にまとめました。 例として、上の図で定義された対称演算を使用した \(C_{3v}) の完全な群乗算表は以下の通りである。 表の1行目に書かれた演算が最初に行われ、次に1列目に書かれた演算が行われます(ただし、 \(\sigma_v\), \(\sigma_v’\), \(\sigma_v”\) を別の順番で名付けると表は変わります)
。