Groepsvermenigvuldiging
Nu gaan we onderzoeken wat er gebeurt als we twee symmetriebewerkingen achter elkaar toepassen. Beschouw als voorbeeld het molecuul NH3, dat behoort tot de puntgroep C3v. Bedenk wat er gebeurt als we een rotatie (C_3) gevolgd door een spiegeling (sigma_v) toepassen. We schrijven deze gecombineerde operatie \(C_3})\(C_3})\(C_3}) (als we symmetrie operaties schrijven, werken ze op het ding direct rechts van hen, net zoals operatoren dat doen in de kwantummechanica – we moeten dus van rechts naar links terugwerken in de notatie om de juiste volgorde te krijgen waarin de operatoren worden toegepast). Zoals we spoedig zullen zien, is de volgorde waarin de operatoren worden toegepast van belang.
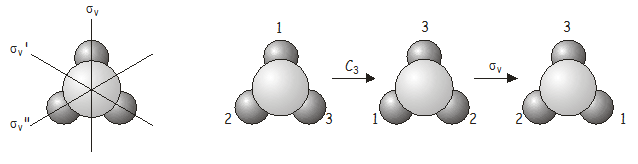
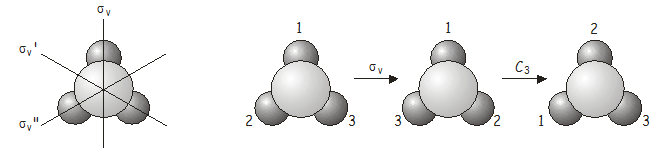
Ook hier is de gecombineerde operatie (C_3)\(\sigma_v’\) equivalent met een andere operatie van de puntengroep, ditmaal \(\sigma_v’\).
Er zijn twee belangrijke punten die door dit voorbeeld worden geïllustreerd:
De effecten van het achter elkaar toepassen van twee symmetriebewerkingen binnen een gegeven puntgroep worden samengevat in groepsvermenigvuldigingstabellen. Als voorbeeld volgt hieronder de volledige groepsvermenigvuldigingstabel voor C_{3v} met de symmetriebewerkingen zoals gedefinieerd in de figuren hierboven. De operaties in de eerste rij van de tabel worden eerst uitgevoerd, gevolgd door die in de eerste kolom (merk op dat de tabel zou veranderen als we de namen \(\sigma_v}), \(\sigma_v’\) en \(\sigma_v”\) in een andere volgorde zouden kiezen).