De volgende definitie van robuuste statistiek komt uit het boek Robust Statistics van P. J. Huber.
… elke statistische procedure moet de volgende wenselijke eigenschappen bezitten:
- Zij moet een redelijk goede (optimale of bijna optimale) efficiëntie hebben bij het veronderstelde model.
- Zij moet robuust zijn in de zin dat kleine afwijkingen van de modelaannames de prestaties slechts in geringe mate mogen schaden. …
- Enigszins grotere afwijkingen van het model mogen geen catastrofe veroorzaken.
De klassieke statistiek richt zich op het eerste van Huber’s punten, het produceren van methoden die optimaal zijn onder voorbehoud van enkele criteria. In dit bericht wordt ingegaan op de canonieke voorbeelden die worden gebruikt om Huber’s tweede en derde punt te illustreren.
Huber’s derde punt wordt gewoonlijk geïllustreerd door het steekproefgemiddelde (gemiddelde) en de steekproefmediaan (middelste waarde). Je kunt bijna de helft van de gegevens in een steekproef op ∞ zetten zonder dat de steekproefmediaan oneindig wordt. Het steekproefgemiddelde daarentegen wordt oneindig als een willekeurige steekproefwaarde oneindig is. Grote afwijkingen van het model, d.w.z. een paar uitschieters, kunnen een catastrofe veroorzaken voor het steekproefgemiddelde, maar niet voor de steekproefmediaan.
Het canonieke voorbeeld bij de bespreking van Huber’s tweede punt gaat terug op John Tukey. Begin met het eenvoudigste schoolvoorbeeld van schatting: gegevens uit een normale verdeling met onbekend gemiddelde en variantie 1, d.w.z. de gegevens zijn normaal(μ, 1) met μ onbekend. De meest efficiënte manier om μ te schatten is het steekproefgemiddelde te nemen, het gemiddelde van de gegevens.
Maar stel nu dat de verdeling van de gegevens niet precies normaal(μ, 1) is, maar in plaats daarvan een mengsel van een standaardnormale verdeling en een normale verdeling met een andere variantie. Stel δ is een klein getal, zeg 0,01, en neem aan dat de gegevens afkomstig zijn van een normale(μ, 1) verdeling met kans 1-δ en de gegevens afkomstig zijn van een normale(μ, σ2) verdeling met kans δ. Deze verdeling wordt een “gecontamineerde normaal” genoemd en het getal δ is de mate van contaminatie. De reden voor het gebruik van het gecontamineerde normale model is dat het een niet-normale verdeling is die er voor het oog normaal uit kan zien.
We zouden het populatiegemiddelde μ kunnen schatten met behulp van het steekproefgemiddelde of de steekproefmediaan. Als de gegevens strikt normaal waren en niet uit een mengsel bestonden, zou het steekproefgemiddelde de meest efficiënte schatter van μ zijn. In dat geval zou de standaardfout ongeveer 25% groter zijn als we de steekproefmediaan gebruikten. Maar als de gegevens van een mengsel afkomstig zijn, kan de steekproefmediaan efficiënter zijn, afhankelijk van de grootte van δ en σ. Hier is een grafiek van de ARE (asymptotische relatieve efficiëntie) van de steekproefmediaan ten opzichte van het steekproefgemiddelde als functie van σ wanneer δ = 0.01.
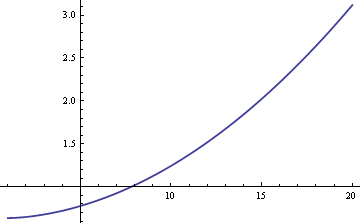
Uit de grafiek blijkt dat voor waarden σ groter dan 8, de steekproefmediaan efficiënter is dan het steekproefgemiddelde. De relatieve superioriteit van de mediaan groeit onbeperkt naarmate σ toeneemt.
Hier volgt een plot van de ARE met σ vastgesteld op 10 en δ variërend tussen 0 en 1.
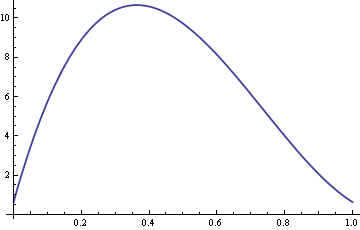
Zo is voor waarden van δ rond 0.4, is de steekproefmediaan meer dan tien keer efficiënter dan het steekproefgemiddelde.
De algemene formule voor de ARE in dit voorbeeld is 2((1 + δ(σ2 – 1)(1 – δ + δ/σ)2)/ π.
Als u er zeker van bent dat uw gegevens normaal zijn zonder verontreiniging of met zeer weinig verontreiniging, dan is het steekproefgemiddelde de meest efficiënte schatter. Maar het kan de moeite waard zijn om het risico te lopen een beetje efficiëntie op te geven in ruil voor de wetenschap dat u het beter zult doen met een robuust model als er significante contaminatie is. Er is meer potentieel verlies bij gebruik van het steekproefgemiddelde als er significante vervuiling is, dan er potentieel winst is bij gebruik van het steekproefgemiddelde als er geen vervuiling is.
Hier is een raadsel in verband met het vervuilde normale voorbeeld. De meest efficiënte schatter voor normale(μ, 1) gegevens is het steekproefgemiddelde. En de meest efficiënte schatter voor normale(μ, σ2) gegevens is ook het steekproefgemiddelde te nemen. Waarom is het dan niet optimaal om het steekproefgemiddelde van het mengsel te nemen?
De sleutel is dat we niet weten of een bepaald monster afkomstig is van de normale(μ, 1) verdeling of van de normale(μ, σ2) verdeling. Als we dat wel wisten, konden we de monsters scheiden, afzonderlijk het gemiddelde berekenen, en de monsters combineren tot een geaggregeerd gemiddelde: het ene gemiddelde vermenigvuldigen met 1-δ, het andere vermenigvuldigen met δ, en optellen. Maar omdat we niet weten welke van de mengselcomponenten tot welke monsters leiden, kunnen we de monsters niet op de juiste manier wegen. (We weten δ waarschijnlijk ook niet, maar dat is een andere zaak.)
Er zijn andere mogelijkheden dan het gebruik van het steekproefgemiddelde of de steekproefmediaan. Bij het getrimde gemiddelde worden bijvoorbeeld enkele van de grootste en kleinste waarden weggelaten en wordt het gemiddelde van de rest genomen. (Soms werken sporten op deze manier, waarbij de hoogste en laagste cijfers van een atleet door de jury worden weggegooid). Hoe meer gegevens aan beide kanten worden weggegooid, hoe meer het getrimde gemiddelde zich gedraagt als de mediaan van de steekproef. Hoe minder gegevens worden weggegooid, hoe meer het zich gedraagt als het steekproefgemiddelde.
Gerelateerd bericht: Efficiëntie van mediaan versus gemiddelde voor Student-t-verdelingen
Voor dagelijkse tips over data science, volg @DataSciFact op Twitter.