Alai

Michael Fowler, UVa Natuurkunde.

Momentum heeft Richting

Zoals we in de vorige lezing hebben besproken, had Descartes, met een beetje hulp van Huygens, zelfs voordat Newton zijn wetten formuleerde, een diepgaande dynamische waarheid ontdekt: bij elke botsing, of in feite bij elke interactie van welke aard dan ook, bleef de totale hoeveelheid “momentum” – een maatstaf voor beweging – altijd hetzelfde. Het momentum van een bewegend voorwerp is gedefinieerd als het product van de massa en de snelheid, en is dus een vector: het heeft grootte en richting. Als je op wrijvingsloze schaatsen staat en je gooit een bal, dan beweeg je achteruit: je momentum is even groot, maar tegengesteld aan dat van de bal, dus het totale momentum (dat van jou plus dat van de bal) blijft nul. Raketten werken op dezelfde manier, door materiaal met hoge snelheid naar buiten te gooien. Ze werken niet door “tegen de lucht te duwen”, ze werken door tegen het materiaal te duwen dat ze naar buiten duwen, net zoals je tegen een bal duwt die je gooit, en die duwt je terug, waardoor je versnelt.

Als je nog steeds vermoedt dat raketten echt tegen de lucht duwen, bedenk dan dat ze in de ruimte net zo goed werken! Toen Goddard, een vroege Amerikaanse raketbouwer (het Goddard Space Flight Center is naar hem genoemd) over raketten in de ruimte sprak, werd algemeen aangenomen dat hij zijn tijd verspilde. Om te citeren uit een redactioneel artikel van de New York Times, geschreven in 1921: “Professor Goddard kent de relatie tussen actie en reactie niet en de noodzaak om iets beters te hebben dan een vacuüm waartegen gereageerd kan worden. Het lijkt hem te ontbreken aan de basiskennis die dagelijks op onze middelbare scholen wordt uitgeschept.” Het is duidelijk dat de redacteuren van de New York Times van die tijd de basiskennis die in deze cursus wordt opgeschept, hebben ontkend!

In feite volgt, zoals we hebben besproken, het behoud van momentum bij een botsing uit de wetten van Newton. Het is echter een algemener, eenvoudiger concept – het hangt helemaal niet af van details van de interacties, enz. Deze eenvoud sprak Einstein kennelijk aan, die ervan overtuigd was dat wanneer de dynamica werd geherformuleerd om er de nieuwe ideeën over tijd en ruimte in op te nemen, behoud van momentum nog steeds waar zou moeten zijn in elk inertiaalstelsel. Dit leidde hem tot enkele verrassende conclusies, zoals we zullen zien.

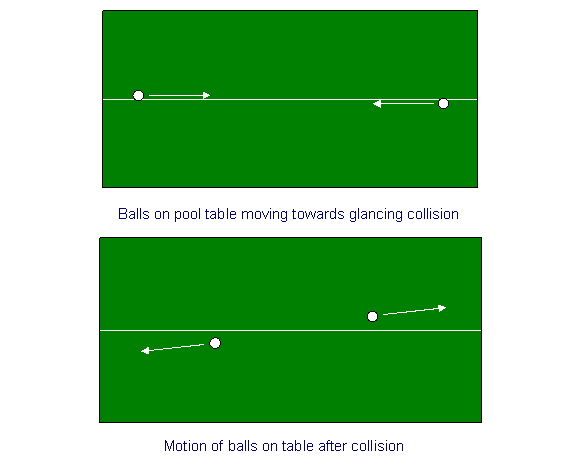
Behoud van momentum op de pooltafel

Laten we als opwarmoefening het behoud van momentum beschouwen voor een botsing van twee ballen op een pooltafel. We trekken een krijtlijn door het midden van de pooltafel, en schieten de ballen dicht bij, maar aan tegenovergestelde kanten van, de krijtlijn vanaf beide uiteinden, met dezelfde snelheid, zodat ze elkaar in het midden zullen raken met een schuine klap, die hun snelheden over een kleine hoek zal draaien. Met andere woorden, als we aanvankelijk zeggen dat hun (gelijke grootte, tegengestelde richting) snelheden evenwijdig waren aan de x-richting – de krijtlijn – dan zullen ze na de botsing ook gelijke en tegengestelde kleine snelheden hebben in de y-richting. (De snelheden in de x-richting zullen heel licht zijn afgenomen).

Een symmetrische botsing tussen ruimteschippen

Nu herhalen we de oefening op een grote schaal. Stel dat we ergens in de ruimte, ver van alle zwaartekrachtvelden, een koord uitzetten van een miljoen mijl lang. (Het zou kunnen liggen tussen onze twee klokken in het tijd-dilatatie experiment). Dit touwtje komt overeen met de krijtlijn op de biljarttafel. Veronderstel nu dat twee identieke ruimteschepen elkaar naderen met gelijke en tegengestelde snelheden evenwijdig aan de koord vanaf de twee uiteinden van de koord, en wel zo dat zij een lichte botsing maken wanneer zij elkaar in het midden ontmoeten. Uit de symmetrie van de situatie blijkt dat het momentum in beide richtingen behouden blijft. In het bijzonder is de snelheid waarmee het ene ruimteschip zich van de snaar verwijdert na de botsing – zijn y-snelheid – gelijk en tegengesteld aan de snelheid waarmee het andere zich van de snaar verwijdert.

Maar beschouw nu deze botsing zoals waargenomen door iemand in een van de ruimteschepen, noem het A. Vóór de botsing ziet hij de snaar heel snel bewegen door het raam, zeg een paar meter verderop. Na de botsing ziet hij dat de koord zich verwijdert, met, zeg, 15 meter per seconde. Dit komt omdat ruimteschip Ah een snelheid loodrecht op de snaar heeft aangenomen van 15 meter per seconde. Ondertussen, aangezien dit een volledig symmetrische situatie is, zou een waarnemer op ruimteschip B zeker afleiden dat haar ruimteschip ook met 15 meter per seconde van de snaar weg bewoog.

Hoe symmetrisch is het?

De cruciale vraag is: hoe snel ziet een waarnemer ruimteschip A ruimteschip B van het koord af bewegen? Laten we aannemen dat ruimteschip B zich ten opzichte van ruimteschip A verwijdert (in de x-richting) met 0,6c. Ten eerste, onthoud dat afstanden loodrecht op de bewegingsrichting niet Lorentz gecontracteerd zijn. Daarom, als de waarnemer in ruimteschip B zegt dat zij 15 meter verder van het koord is verwijderd in een tijdsinterval van één seconde, zal de waarnemer die deze beweging bekijkt vanuit ruimteschip A het eens zijn over de 15 meter – maar het oneens zijn over de één seconde! Hij zal zeggen dat haar klokken traag lopen, dus zoals gemeten door zijn klokken zal er 1,25 seconde zijn verstreken terwijl zij 15 meter in de y-richting beweegt.

Daaruit volgt dat, als gevolg van de tijddilatatie, deze botsing gezien vanuit ruimteschip A niet leidt tot gelijke en tegengestelde snelheden voor de twee ruimteschepen in de y-richting. Aanvankelijk bewogen beide ruimteschepen evenwijdig aan de x-as, er was een nulmoment in de y-richting. Hoe kunnen we dan beweren dat het totale momentum in de y-richting nul is na de botsing, als de identieke ruimteschepen geen gelijke en tegengestelde snelheden hebben?

Einstein redt behoud van momentum

Einstein was er zo zeker van dat behoud van momentum altijd moet gelden, dat hij het redde met een gewaagde hypothese: de massa van een voorwerp moet afhangen van zijn snelheid! In feite moet de massa zodanig met de snelheid toenemen, dat de lagere y-richting snelheid ten gevolge van de tijddilatatie teniet wordt gedaan. Dat wil zeggen dat als een voorwerp in rust een massa m heeft en met een snelheid v beweegt, het een traagheid zal hebben die overeenkomt met een “relativistische massa” m rel =m/ 1-( v 2 / c 2 ) . Dan wordt het momentum

p → = m rel v → =m v → / 1-( v 2 / c 2 ) .

Merk op dat deze relativistische massatoename bij gewone snelheden een onmerkbaar klein effect is, maar naarmate een voorwerp de vliegsnelheid nadert, neemt de massa onbeperkt toe!

Massa neemt werkelijk toe met snelheid

Om te besluiten dat massa’s van voorwerpen afhankelijk moeten zijn van snelheid lijkt dit een zware prijs om behoud van momentum te redden! Het is echter een voorspelling die niet moeilijk experimenteel te controleren is. De eerste bevestiging kwam in 1908, toen snelle elektronen in een vacuümbuis werden afgebogen. In feite, hebben de elektronen in een oude stijl kleurenTV buis ongeveer een half percent meer inertie dan elektronen in rust, en dit moet worden toegestaan bij de berekening van de magnetische velden die worden gebruikt om hen naar het scherm te leiden.

In moderne deeltjesversnellers worden veel krachtiger elektrische velden gebruikt om elektronen, protonen en andere deeltjes te versnellen. In de praktijk is gebleken dat deze deeltjes steeds grotere krachten nodig hebben voor verdere versnelling naarmate de lichtsnelheid wordt benaderd. Bijgevolg is de lichtsnelheid een natuurlijke absolute snelheidslimiet. Deeltjes worden versneld tot snelheden waarbij hun relativistische massa duizenden malen groter is dan hun in rust gemeten massa, die gewoonlijk de “rustmassa” wordt genoemd.

…of toch niet?

Eigenlijk is er een voortdurende discussie onder natuurkundigen over dit concept van relativistische massa. Het debat is grotendeels semantisch: niemand betwijfelt dat de juiste uitdrukking voor het moment van een deeltje met een rustmassa m dat zich verplaatst met een snelheid v → is p → = m 1- v 2 / c 2 v → . Maar vooral deeltjesfysici, van wie velen hun leven besteden aan het meten van rustmassa’s van deeltjes met grote nauwkeurigheid, zijn er niet happig op om dit te schrijven als p → = m rel v → . Ze houden niet van het idee van een variabele massa. Ten eerste zou het de indruk kunnen wekken dat een deeltje, naarmate het sneller gaat, in omvang toeneemt, of dat op zijn minst zijn inwendige structuur op de een of andere manier verandert. In feite ondergaat een relativistisch deeltje gewoon Lorentz-contractie langs de bewegingsrichting, net als ieder ander. Het gaat van een bolvorm naar een schijfvorm met dezelfde transversale straal.

Dus hoe kan deze “massatoename” worden begrepen? Zoals gewoonlijk had Einstein het bij het rechte eind: hij merkte op dat elke vorm van energie een traagheid bezit. De kinetische energie zelf heeft traagheid. Nu is “traagheid” een bepalende eigenschap van massa. De andere fundamentele eigenschap van massa is dat het gravitationeel aantrekt. Doet deze kinetische energie dat? Om het antwoord te zien, beschouw een bol gevuld met gas. Deze zal buiten zichzelf een sferisch symmetrisch gravitatieveld opwekken, waarvan de sterkte evenredig is met de totale massa. Als we nu het gas verhitten, zullen de gasdeeltjes deze toegenomen (relativistische) massa hebben, die overeenkomt met hun toegenomen kinetische energie, en het externe gravitatieveld zal evenredig zijn toegenomen. (Niemand twijfelt aan een van beide.)

Dus de “relativistische massa” heeft inderdaad de twee basiseigenschappen van massa: traagheid en gravitationele aantrekkingskracht. (Zoals in de volgende colleges duidelijk zal worden, is deze relativistische massa niets anders dan de totale energie, waarbij de rustmassa nu zelf als energie wordt gezien.)

Op een meer triviaal niveau maken sommige docenten bezwaar tegen de invoering van relativistische massa, omdat zij vrezen dat de leerlingen zullen aannemen dat de kinetische energie van een relativistisch bewegend deeltje gewoon 1 2 m v → 2 is met gebruikmaking van de relativistische massa – dat is niet het geval, zoals we zo dadelijk zullen zien.

Vooropmerking: Voor iedereen die misschien eens doorgaat naar een wiskundig verfijnde behandeling, moet worden toegevoegd dat de rustmassa een belangrijke rol speelt als onveranderlijke factor bij het overgaan van het ene referentiekader naar het andere, maar de hier gebruikte “relativistische massa” is eigenlijk gewoon de eerste component (de energie) van de vierdimensionale energie-momentumvector van een deeltje, en is dus geen invariant.

Kinetische energie en massa voor zeer snelle deeltjes

Laten we eens kijken naar de kinetische energie van een van deze deeltjes die dicht bij de lichtsnelheid reizen. Herinner u dat we in een eerdere lezing ontdekten dat de kinetische energie van een gewone niet-relativistische (d.w.z. langzaam bewegende) massa m 1 2 m v 2 was. De manier waarop we dat deden was door na te gaan hoeveel werk we moesten verrichten om de massa over een bepaalde hoogte te tillen: we moesten een kracht uitoefenen gelijk aan zijn gewicht W om hem over hoogte h te tillen, waarbij de totale verrichte arbeid, of verbruikte energie, kracht x afstand, Wh was. Toen het voorwerp weer naar beneden viel, verrichtte de zwaartekracht, W, precies evenveel arbeid Wh op het vallende voorwerp, maar deze keer werd de arbeid gebruikt om het voorwerp te versnellen, zodat het kinetische energie kreeg. Omdat we weten hoe snel vallende voorwerpen snelheid oppikken, konden we concluderen dat de kinetische energie 1 2 m v 2 was. (Voor details, zie de vorige lezing.)

Meer in het algemeen hadden we de massa kunnen versnellen met een willekeurige constante kracht F, en de door de kracht verrichte arbeid (kracht xafstand) kunnen vinden om de massa vanuit stilstand op snelheid v te brengen. De kinetische energie van de massa, E= 1 2 m v 2 , is precies gelijk aan de arbeid die door de kracht wordt verricht om de massa tot die snelheid te brengen. (Op soortgelijke wijze kan worden aangetoond dat, indien een kracht wordt uitgeoefend op een deeltje dat zich reeds met een snelheid u verplaatst, en het wordt versneld tot een snelheid v, de benodigde arbeid 1 2 m v 2 – 1 2 m u 2 bedraagt).

Het is interessant om te proberen de oefening te herhalen voor een deeltje dat zich zeer dicht bij de lichtsnelheid beweegt, zoals de deeltjes in de in de vorige paragraaf genoemde versnellers. De tweede wet van Newton, in de vorm

Kracht = snelheid van verandering van momentum

is nog steeds waar, maar dicht bij de lichtsnelheid verandert de snelheid verwaarloosbaar terwijl de kracht blijft werken – in plaats daarvan neemt de massa toe! Daarom kunnen we uitstekend benaderend schrijven:

Kracht = (snelheid van massaverandering) x c

waarbij zoals gebruikelijk c de lichtsnelheid is. Om specifieker te worden, stel dat we een constante kracht F hebben die op een deeltje duwt. Op een bepaald moment heeft het deeltje massa M, en een snelheid die zeer dicht ligt bij c. Een seconde later, omdat de kracht op het deeltje blijft werken, en dus zijn impuls volgens de tweede wet van Newton toeneemt, zal het deeltje massa M+m hebben, zeg, waarbij m de toename in massa is als gevolg van de door de kracht verrichte arbeid.

Wat is de toename van de kinetische energie E van het deeltje gedurende die periode van één seconde? Naar analogie van het on-relativistische geval, zoals hierboven beschreven, is dat gewoon de arbeid van de kracht gedurende die periode. Aangezien de massa van het deeltje in één seconde met m verandert, is m ook de snelheid waarmee de massa verandert. Daarom kunnen we uit de tweede wet van Newton in de vorm

Kracht = (snelheid van verandering van massa) x c,

schrijven

Kracht =mc.

De toename van de kinetische energie E in de periode van één seconde is gewoon het werk van de kracht,

E= kracht x afstand.

Omdat het deeltje zich hoofdzakelijk met de snelheid van de vlucht verplaatst, is de afstand waarover de kracht in de periode van één seconde werkt slechts c meter, c=3× 10 8 .

Dus de totale arbeid die de kracht in die seconde verricht is kracht x afstand =mc×c=m c 2 .

Hieruit volgt dat het verband tussen de toename van de massa van het relativistische deeltje en de toename van zijn kinetische energie is:

E=m c 2 .

Kinetische energie en massa voor trage deeltjes

Om de wetten van Newton in alle traagheidsframes te laten gelden, moesten we uitgaan van een toename van de massa met de snelheid met de factor 1/ 1-( v 2 / c 2 ) . Dit impliceert dat zelfs een langzaam bewegend voorwerp een kleine toename in massa heeft als het beweegt!

Hoe verhoudt die kleine toename zich tot de kinetische energie? Beschouw een massa M, bewegend met snelheid v, veel minder dan de lichtsnelheid. Zijn kinetische energie E= 1 2 M v 2 , zoals hierboven besproken. Haar massa is M/ 1-( v 2 / c 2 ), die we kunnen schrijven als M+m. Wat is m ?

Omdat we het hebben over snelheden waarmee we vertrouwd zijn, zoals bij een straalvliegtuig, waar v/c, heel klein is, kunnen we wat eenvoudige wiskundige trucjes gebruiken om het wat gemakkelijker te maken.

De eerste is een goede benadering voor de vierkantswortel van 1-x als x veel kleiner is dan één:

1-x ≅1- 1 2 x voor x≪1.

Dit kun je gemakkelijk met je rekenmachine controleren: probeer x= 1 100 , je vindt 99 100 =0,994987… wat heel dicht bij 1- 1 2 1 100 =0,995 ligt !

De volgende benadering is

1 1-x ≅1+x voor x≪1.

Dit is ook gemakkelijk na te gaan: neem weer x= 1 100 : 1 1-x = 1 99 100 = 100 99 =1.01010… ,en 1+x= 101 100 =1.01.

Gebruik makend van deze benaderingen met x=v/c, kunnen we 1-( v 2 / c 2 ) benaderen als 1- 1 2 ( v 2 / c 2 ) , en dan 1/( 1- 1 2 ( v 2 / c 2 ) ) als 1+ 1 2 ( v 2 / c 2 ) .

Dit betekent dat de totale massa bij snelheid v

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ),

en schrijven we dit als M+m, dan zien we dat de massatoename m gelijk is aan 1 2 M v 2 / c 2 .

Dit betekent dat – nogmaals – de massatoename m is gerelateerd aan de kinetische energie E door E=m c 2 .

In feite is het niet moeilijk om met een beetje rekenwerk aan te tonen, dat over het hele snelheidsbereik van nul tot zo dicht mogelijk bij de lichtsnelheid, een bewegend deeltje een massatoename ondervindt die gerelateerd is aan zijn kinetische energie met E=m c 2 . Om te begrijpen waarom dit in het dagelijks leven niet wordt opgemerkt, kunt u een voorbeeld nemen, zoals een straalvliegtuig van 100 ton dat met 2000 km per uur vliegt. 100 ton is 100.000 kilogram, 2.000 mph is ongeveer 1.000 meter per seconde. Dat is een kinetische energie 1 2 M v 2 van ½ ×1011joule, maar de overeenkomstige massaverandering van het vliegtuig naar beneden met de factor c 2 , 9× 10 16 , waardoor een werkelijke massatoename van ongeveer een halve milligram, niet al te gemakkelijk te detecteren!

E = mc2

We hebben hierboven gezien dat wanneer een kracht een lichaam versnelt om het kinetische energie te geven, de massa van het lichaam toeneemt met een hoeveelheid die gelijk is aan de totale door de kracht verrichte arbeid, de overgedragen energie E, gedeeld door c 2 . Hoe zit het als een kracht op een lichaam werkt dat het niet versnelt, dus er is geen toename van kinetische energie? Bijvoorbeeld, wat als ik iets optil in een gelijkmatig tempo, waardoor het potentiële energie krijgt? Het blijkt dat er ook in dit geval een massatoename is, gegeven door E=m c 2 , uiteraard onmeetbaar klein voor alledaagse voorwerpen.

Het is echter wel een meetbaar en belangrijk effect in de kernfysica. Het heliumatoom bijvoorbeeld heeft een kern met twee protonen en twee neutronen, die door een sterke kern-aantrekkingskracht sterk aan elkaar zijn gebonden. Indien van buitenaf voldoende kracht wordt uitgeoefend, kan deze kern worden gesplitst in twee “zware waterstofkernen”, die elk één proton en één neutron hebben. Er moet veel externe energie worden gebruikt om deze scheiding te bereiken, en men ontdekt dat de totale massa van de twee zware waterstofkernen meetbaar (ongeveer een half procent) zwaarder is dan de oorspronkelijke heliumkern. Deze extra massa, vermenigvuldigd met c 2 , is precies gelijk aan de energie die nodig is om de heliumkern in tweeën te splitsen. Nog belangrijker is dat deze energie kan worden teruggewonnen door de twee zware waterstofnuclei met elkaar te laten botsen en weer een heliumkern te laten vormen. (Ze zijn beide positief geladen, dus stoten ze elkaar af, en moeten vrij snel samenkomen om deze afstoting te overwinnen en zo dicht bij elkaar te komen dat de veel sterkere nucleaire aantrekkingskracht optreedt). Dit is de basiskrachtbron van de waterstofbom, en van de zon.

Het blijkt dat alle vormen van energie, kinetische en verschillende soorten potentiële energie, een bijbehorende massa hebben, gegeven door E=m c 2 . Voor kernreacties is de massaverandering meestal van de orde van een duizendste van de totale massa, en gemakkelijk meetbaar. Voor chemische reacties is de verandering van de orde van een miljardste van de totale massa, en momenteel niet meetbaar.

vorige index