Group Multiplication
Teraz zbadamy, co się stanie, gdy zastosujemy dwie operacje symetrii po kolei. Jako przykład rozważmy cząsteczkę NH_3, która należy do grupy punktowej C_{3v}. Zastanówmy się, co się stanie, jeśli zastosujemy rotację (C_3), a następnie odbicie (sigma_v). Zapisujemy tę połączoną operację \(\) (w zapisie operacje symetrii działają na rzeczach znajdujących się bezpośrednio po ich prawej stronie, tak jak operatory w mechanice kwantowej – musimy zatem pracować wstecz od prawej do lewej strony notacji, aby uzyskać poprawną kolejność, w jakiej operatory są stosowane). Jak wkrótce zobaczymy, kolejność stosowania operacji jest istotna.
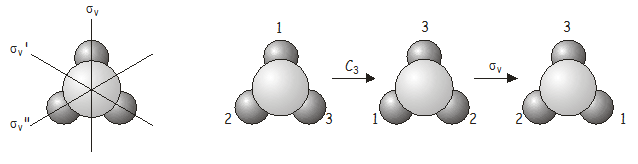
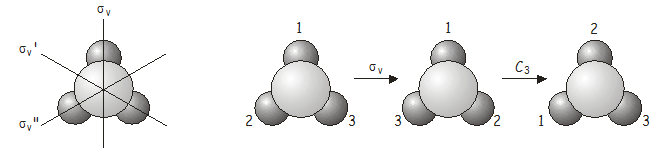
Ponownie, operacja łączna \(C_3\) jest równoważna innej operacji grupy punktowej, tym razem \(\).
Istnieją dwa ważne punkty, które są zilustrowane przez ten przykład:
Efekty zastosowania dwóch operacji symetrii kolejno w danej grupie punktowej są podsumowane w tablicach mnożenia grup. Jako przykład, pełna tabliczka mnożenia grupowego dla C_{3v}} z wykorzystaniem operacji symetrii zdefiniowanych na powyższych rysunkach jest pokazana poniżej. W pierwszej kolejności wykonywane są operacje zapisane w pierwszym wierszu tabeli, a następnie te zapisane w pierwszej kolumnie (zauważmy, że tabela uległaby zmianie, gdybyśmy zdecydowali się nadać nazwy \(\sigma_v\), \(\sigma_v’\) i \(\sigma_v’\) w innej kolejności).