Następująca definicja solidnej statystyki pochodzi z książki P. J. Hubera Robust Statistics.
… każda procedura statystyczna powinna posiadać następujące pożądane cechy:
- Powinna mieć w miarę dobrą (optymalną lub prawie optymalną) efektywność przy założonym modelu.
- Powinna być odporna w tym sensie, że małe odchylenia od założeń modelu powinny tylko nieznacznie pogarszać jej efektywność. …
- Nieco większe odchylenia od modelu nie powinny powodować katastrofy.
Klasyczna statystyka skupia się na pierwszym z punktów Hubera, produkując metody, które są optymalne pod warunkiem spełnienia pewnych kryteriów. Ten post patrzy na kanoniczne przykłady używane do zilustrowania drugiego i trzeciego punktu Hubera.
Trzeci punkt Hubera jest zwykle ilustrowany przez średnią próbkę (średnią) i medianę próbki (wartość środkową). Możesz ustawić prawie połowę danych w próbce na ∞ bez powodowania, że mediana próbki stanie się nieskończona. Średnia z próby, z drugiej strony, staje się nieskończona, jeśli jakakolwiek wartość próby jest nieskończona. Duże odchylenia od modelu, tj. kilka wartości odstających, mogą spowodować katastrofę dla średniej próbki, ale nie dla mediany próbki.
Kanoniczny przykład przy omawianiu drugiego punktu Hubera sięga Johna Tukey’a. Zacznij od najprostszego podręcznikowego przykładu estymacji: dane z rozkładu normalnego z nieznaną średnią i wariancją 1, tj. dane są normalne(μ, 1) z μ nieznanym. Najbardziej efektywnym sposobem oszacowania μ jest wzięcie średniej z próby, średniej z danych.
Ale teraz załóżmy, że rozkład danych nie jest dokładnie normalny(μ, 1), ale zamiast tego jest mieszaniną standardowego rozkładu normalnego i rozkładu normalnego z inną wariancją. Niech δ będzie małą liczbą, powiedzmy 0.01, i załóżmy, że dane pochodzą z rozkładu normalnego(μ, 1) z prawdopodobieństwem 1-δ, a dane pochodzą z rozkładu normalnego(μ, σ2) z prawdopodobieństwem δ. Taki rozkład nazywamy „zanieczyszczonym normalnym”, a liczba δ jest wielkością zanieczyszczenia. Powodem użycia modelu zanieczyszczonego normalnego jest to, że jest to rozkład nienormalny, który może wyglądać normalnie dla oka.
Możemy oszacować średnią populacji μ używając albo średniej z próby albo mediany z próby. Jeśli dane byłyby ściśle normalne, a nie mieszane, średnia z próby byłaby najbardziej efektywnym estymatorem μ. W tym przypadku błąd standardowy byłby o około 25% większy, gdybyśmy użyli mediany z próby. Jeśli jednak dane pochodzą z mieszaniny, mediana próby może być bardziej efektywna, w zależności od wielkości δ i σ. Oto wykres ARE (asymptotycznej efektywności względnej) mediany próby w porównaniu ze średnią próbą w funkcji σ, gdy δ = 0.01.
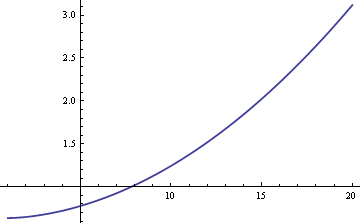
Z wykresu wynika, że dla wartości σ większych od 8, mediana próbki jest bardziej efektywna niż średnia próbki. Względna wyższość mediany rośnie bez ograniczeń wraz ze wzrostem σ.
Tutaj wykres ARE z σ ustalonym na 10 i δ zmieniającym się w zakresie od 0 do 1.
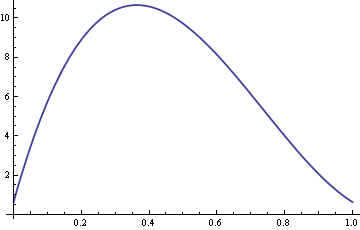
Więc dla wartości δ około 0.4, mediana próbki jest ponad dziesięć razy bardziej efektywna niż średnia próbki.
Ogólny wzór na ARE w tym przykładzie to 2((1 + δ(σ2 – 1)(1 – δ + δ/σ)2)/ π.
Jeśli jesteś pewien, że twoje dane są normalne bez zanieczyszczeń lub z bardzo małymi zanieczyszczeniami, wtedy średnia próbki jest najbardziej efektywnym estymatorem. Ale może warto zaryzykować rezygnację z odrobiny efektywności w zamian za wiedzę, że lepiej będzie działać z solidnym modelem, jeśli wystąpi znaczne zanieczyszczenie. Istnieje większy potencjał straty przy użyciu średniej z próby, gdy występuje znaczące zanieczyszczenie, niż potencjalny zysk przy użyciu średniej z próby, gdy nie ma zanieczyszczenia.
Jest pewien problem związany z zanieczyszczonym normalnym przykładem. Najbardziej efektywnym estymatorem dla danych normal(μ, 1) jest średnia z próby. A najbardziej efektywnym estymatorem dla danych normal(μ, σ2) jest również wzięcie średniej z próby. Dlaczego więc nie jest optymalne przyjęcie średniej z próby mieszanki? Kluczem jest to, że nie wiemy, czy dana próba pochodzi z rozkładu normalnego(μ, 1) czy z rozkładu normalnego(μ, σ2). Gdybyśmy wiedzieli, moglibyśmy posegregować próbki, uśrednić je osobno i połączyć próbki w średnią zbiorczą: mnożąc jedną średnią przez 1-δ, mnożąc drugą przez δ i dodając. Ale ponieważ nie wiemy, które składniki mieszaniny prowadzą do których próbek, nie możemy odpowiednio zważyć próbek. (Prawdopodobnie nie znamy również δ, ale to inna sprawa.)
Istnieją inne opcje niż użycie średniej lub mediany próbki. Na przykład, średnia obcięta wyrzuca niektóre z największych i najmniejszych wartości, a następnie uśrednia wszystko inne. (Czasami sporty działają w ten sposób, wyrzucając najwyższe i najniższe oceny sportowca od sędziów). Im więcej danych wyrzuca się na każdym końcu, tym bardziej średnia obcięta zachowuje się jak mediana próby. Im mniej danych wyrzuconych, tym bardziej zachowuje się jak średnia próbna.
Related post: Efficiency of median versus mean for Student-t distributions
Dla codziennych wskazówek na temat nauki o danych, śledź @DataSciFact na Twitterze.
.