Alai

Michael Fowler,fizyka UVa.

Momentum ma kierunek

Jak omawialiśmy w ostatnim wykładzie, jeszcze zanim Newton sformułował swoje prawa, Kartezjusz, z niewielką pomocą Huygensa, odkrył głęboką prawdę dynamiki: w każdym zderzeniu, a właściwie w każdej interakcji dowolnego rodzaju, całkowita ilość „pędu” – miary ruchu – zawsze pozostawała taka sama. Pęd poruszającego się obiektu definiuje się jako iloczyn masy i prędkości, a więc jest on wektorem: ma wielkość i kierunek. Jeśli stoisz na łyżwach bez tarcia i rzucisz piłkę, poruszasz się do tyłu: masz pęd równy co do wielkości, ale przeciwny kierunek do pędu piłki, więc całkowity pęd (twój plus piłki) pozostaje równy zeru. Rakiety działają w ten sam sposób, wyrzucając materiał z dużą prędkością. Nie działają one poprzez „pchanie się w powietrze”, działają poprzez pchanie się w materiał, który wypychają, tak jak pchasz się w piłkę, którą rzucasz, a ona pcha cię do tyłu, powodując twoje przyspieszenie.

Jeśli nadal podejrzewasz, że naprawdę rakiety pchają się przeciwko powietrzu, pamiętaj, że działają tak samo dobrze w przestrzeni kosmicznej! W rzeczywistości, powszechnie uważano, że kiedy Goddard, wczesny amerykański rakieciarz (Centrum Lotów Kosmicznych Goddarda jest nazwane jego imieniem) mówił o rakietach w kosmosie, marnował swój czas. Cytując za artykułem redakcyjnym New York Timesa napisanym w 1921 roku: „Profesor Goddard nie zna związku między akcją i reakcją oraz potrzeby posiadania czegoś lepszego niż próżnia, przeciwko czemu można by reagować. Wydaje się, że brakuje mu podstawowej wiedzy przekazywanej codziennie w naszych szkołach średnich”. Oczywiście, New York Times redaktorzy czasopism w tym czasie podziwiał podstawową wiedzę, która jest podawana w tym kursie!

W rzeczywistości, jak rozmawialiśmy, zachowanie pędu w zderzeniu wynika z praw Newtona. Jest to jednak bardziej ogólne, prostsze pojęcie – nie zależy w ogóle od szczegółów oddziaływań itp. Ta prostota najwyraźniej spodobała się Einsteinowi, który był przekonany, że gdy dynamika zostanie przeformułowana tak, by uwzględnić nowe idee dotyczące czasu i przestrzeni, zachowanie pędu powinno nadal być prawdziwe w każdej ramie inercyjnej. To doprowadziło go do pewnych zaskakujących wniosków, jak zobaczymy.

Zachowanie pędu na stole bilardowym

Jako ćwiczenie na rozgrzewkę rozważmy zachowanie pędu dla zderzenia dwóch kul na stole bilardowym. Narysujmy linię kredową pośrodku stołu bilardowego i wystrzelmy bile blisko, ale po przeciwnych stronach linii kredowej, z obu jej końców, z tą samą prędkością, tak, że uderzą się one pośrodku, co obróci ich prędkości o mały kąt. Innymi słowy, jeśli początkowo mówimy, że ich prędkości (równe wielkości, przeciwne kierunki) były równoległe do kierunku x – linii kredowej – to po zderzeniu będą one miały również równe i przeciwne małe prędkości w kierunku y (prędkości w kierunku x zmniejszą się bardzo nieznacznie).

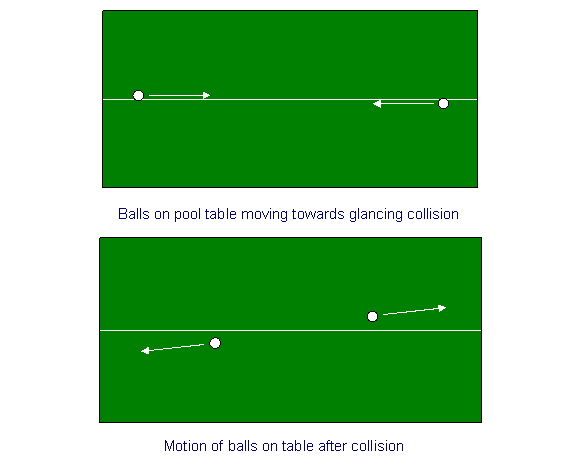
Zderzenie symetrycznych statków kosmicznych

Powtórzmy teraz to ćwiczenie w większej skali. Przypuśćmy, że gdzieś w przestrzeni kosmicznej, z dala od jakichkolwiek pól grawitacyjnych, ustawimy sznurek o długości miliona mil. (Mógłby on znajdować się pomiędzy naszymi dwoma zegarami w eksperymencie dylatacji czasu). Ten sznurek odpowiada linii kredowej na stole bilardowym. Przypuśćmy teraz, że mamy dwa identyczne statki kosmiczne zbliżające się do siebie z równymi i przeciwnymi prędkościami równolegle do sznurka z dwóch końców sznurka, wycelowane tak, że doznają lekkiego zderzenia, gdy spotkają się w środku. Z symetrii sytuacji wynika, że pęd jest zachowany w obu kierunkach. W szczególności szybkość, z jaką jeden statek oddala się od sznurka po zderzeniu – jego prędkość y – jest równa i przeciwna szybkości, z jaką drugi statek oddala się od sznurka.

A teraz rozważmy to zderzenie jako obserwowane przez kogoś w jednym ze statków kosmicznych, nazwijmy go A. Przed zderzeniem widzi on sznurek poruszający się bardzo szybko przy oknie, powiedzmy kilka metrów dalej. Po zderzeniu widzi on, że sznurek oddala się z prędkością, powiedzmy, 15 metrów na sekundę. Dzieje się tak dlatego, że statek kosmiczny Ah nabrał prędkości prostopadłej do sznurka, wynoszącej 15 metrów na sekundę. Tymczasem, ponieważ jest to sytuacja całkowicie symetryczna, obserwator na statku B z pewnością wywnioskowałby, że jego statek również oddalał się od sznurka z prędkością 15 metrów na sekundę.

Jak bardzo jest to symetryczne?

Kluczowe pytanie brzmi: jak szybko obserwator inspirujący statek kosmiczny A widzi, że statek kosmiczny B oddala się od sznurka? Załóżmy, że względem statku kosmicznego A, statek kosmiczny B oddala się (w kierunku x) z prędkością 0,6c. Po pierwsze, przypomnijmy, że odległości prostopadłe do kierunku ruchu nie podlegają kontrakcji Lorentza. Dlatego, gdy obserwator w statku kosmicznym B powie, że oddalił się od sznurka o 15 metrów w odstępie jednej sekundy, obserwator obserwujący ten ruch ze statku kosmicznego A zgodzi się co do 15 metrów – ale nie zgodzi się co do jednej sekundy! Powie, że jej zegary działają wolno, więc według jego zegarów upłynie 1,25 sekundy, gdy ona przesunie się o 15 metrów w kierunku y.

Wynika z tego, że w wyniku dylatacji czasu, ta kolizja widziana ze statku kosmicznego A nie powoduje równych i przeciwnych prędkości dla dwóch statków kosmicznych w kierunku y. Początkowo oba statki poruszały się równolegle do osi x, w kierunku y było zerowe momentum. Jak więc możemy twierdzić, że po zderzeniu istnieje zerowy całkowity pęd w kierunku y, skoro identyczne statki kosmiczne nie mają równych i przeciwnych prędkości?

Einstein ratuje zachowanie pędu

Einstein był tak pewny, że zachowanie pędu musi być zawsze zachowane, że uratował je za pomocą śmiałej hipotezy: masa obiektu musi zależeć od jego prędkości! W rzeczywistości masa musi wzrastać wraz z prędkością w taki sposób, aby zniwelować mniejszą prędkość w kierunku y wynikającą z dylatacji czasu. Oznacza to, że jeżeli obiekt w spoczynku ma masę m, to poruszając się z prędkością v będzie miał bezwładność odpowiadającą „masie relatywistycznej” m rel =m/ 1-( v 2 / c 2 ) .Wtedy moment pędu staje się

p → = m rel v → =m v → / 1-( v 2 / c 2 ) .

Zauważmy, że ten relatywistyczny wzrost masy jest niewykrywalnie mały przy zwykłych prędkościach, ale gdy obiekt zbliża się do prędkości lotu, masa rośnie bez ograniczeń!

Mass Really Does Increase with Speed

Deciding that masses of objects must depend on speed likeethis seems a heavy price to pay to rescue conservation of momentum! Jest to jednak przewidywanie, które nietrudno sprawdzić doświadczalnie. Pierwsze potwierdzenie przyszło w 1908 r., poprzez odchylenie szybkich elektronów w rurze próżniowej. W rzeczywistości, elektrony w starym stylu kolorowej lampy telewizyjnej mają około pół procenta więcej bezwładności niż elektrony w spoczynku, i to musi być dozwolone w obliczeniach pól magnetycznych używanych do kierowania ich do ekranu.

Dużo bardziej dramatycznie, w nowoczesnych akceleratorów cząstek bardzopowerful pola elektryczne są używane do przyspieszania elektronów, protonów i innych cząstek. W praktyce okazuje się, że cząstki te potrzebują coraz większych sił do dalszego przyspieszania w miarę zbliżania się do prędkości światła. W związku z tym prędkość światła jest naturalną, absolutną granicą prędkości. Cząstki są przyspieszane do prędkości, przy których ich masa relatywistyczna jest tysiące razy większa niż ich masa mierzona w spoczynku, zwykle nazywana „masą spoczynkową”.

…Or Does It?

Actually, there is continuing debate among physicistsconcerning this concept of relativistic mass. Debata ta jest w dużej mierze semantyczna: nikt nie wątpi, że poprawnym wyrażeniem na pęd cząstki o masie spoczynkowej m poruszającej się z prędkością v → jest p → = m 1- v 2 / c 2 v → . Jednak szczególnie fizycy cząstek elementarnych, z których wielu spędza życie na precyzyjnych pomiarach mas spoczynkowych cząstek, nie są skorzy do zapisywania tego wyrażenia jako p → = m rel v → . Nie podoba im się pomysł zmiennej masy. Po pierwsze, może to sprawiać wrażenie, że w miarę przyspieszania cząstka zwiększa swoje rozmiary, a przynajmniej zmienia się jej wewnętrzna struktura. W rzeczywistości relatywistyczna cząstka po prostu ulega skurczeniu Lorentza wzdłuż kierunku ruchu, jak wszystko inne. Przechodzi ona od kształtu kulistego do kształtu dysku o tym samym promieniu poprzecznym.

Jak więc można zrozumieć ten „wzrost masy”? Jak zwykle Einstein miał rację: zauważył, że każda forma energii posiada bezwładność. Energia kinetyczna sama w sobie ma bezwładność. Teraz „bezwładność” jest cechą definiującą masę. Inną fundamentalną własnością masy jest to, że przyciąga ona grawitacyjnie. Czy ta energia kinetyczna to robi? Aby zobaczyć odpowiedź, rozważmy kulę wypełnioną gazem. Będzie ona wytwarzać sferycznie symetryczne pole grawitacyjne na zewnątrz siebie, o sile proporcjonalnej do całkowitej masy. Jeśli teraz podgrzejemy gaz, cząsteczki gazu będą miały zwiększoną (relatywistyczną) masę, odpowiadającą ich zwiększonej energii kinetycznej, a zewnętrzne pole grawitacyjne zwiększy się proporcjonalnie. (Nikt w to nie wątpi.)

Tak więc „relatywistyczna masa” rzeczywiście posiada dwie podstawowe własności masy: bezwładność i przyciąganie grawitacyjne. (Jak stanie się jasne w następnych wykładach, ta relatywistyczna masa jest niczym innym jak całkowitą energią, przy czym masa spoczynkowa jest teraz postrzegana jako energia.)

Na bardziej trywialnym poziomie, niektórzy nauczyciele sprzeciwiają się wprowadzaniu masy relatywistycznej, ponieważ obawiają się, że studenci będą zakładać, że energia kinetyczna relatywistycznie poruszającej się cząstki jest po prostu 1 2 m v → 2 przy użyciu masy relatywistycznej – nie jest tak, jak zobaczymy wkrótce.

Przypis: Dla każdego, kto mógłby kiedyś przejść do bardziej wyrafinowanego matematycznie traktowania, należy dodać, że masa spoczynkowa odgrywa ważną rolę jako niezmiennik przy przechodzeniu z jednego układu odniesienia do drugiego, ale „masa relatywistyczna” używana tutaj jest tak naprawdę tylko pierwszą składową (energią) czterowymiarowego wektora energia-momentum cząstki, a więc nie jest niezmiennikiem.

Energia kinetyczna i masa dla bardzo szybkich cząstek

Pomyślmy o energii kinetycznej jednej z cząstek poruszających się z prędkością bliską prędkości światła. Przypomnijmy, że we wcześniejszym wykładzie stwierdziliśmy, że energia kinetyczna zwykłej nierelatywistycznej (tzn. wolno poruszającej się) masy m wynosi 1 2 m v 2 . Zrobiliśmy to, rozważając, ile pracy trzeba było wykonać, aby podnieść ją na pewną wysokość: musieliśmy wywrzeć siłę równą jej masie W, aby podnieść ją na wysokość h, przy czym całkowita wykonana praca, czyli zużyta energia, wynosiła siła x odległość, Wh. Gdy spadał z powrotem w dół, siła grawitacji, W, wykonała dokładnie taką samą pracę Wh nad spadającym obiektem, ale tym razem praca ta została wydatkowana na przyspieszenie obiektu, aby nadać mu energię kinetyczną. Ponieważ wiemy, z jaką prędkością spadające obiekty nabierają prędkości, mogliśmy wywnioskować, że energia kinetyczna wynosi 1 2 m v 2 . (Szczegóły w poprzednim wykładzie.)

Więcej, mogliśmy przyspieszyć masę dowolną stałą siłą F i znaleźć pracę wykonaną przez tę siłę (siła x odległość), aby doprowadzić ją do prędkości v ze startu stojącego. Energia kinetyczna masy, E= 1 2 m v 2 , jest dokładnie równa pracy wykonanej przez siłę w doprowadzeniu masy do tej prędkości. (W podobny sposób można wykazać, że jeśli do cząstki poruszającej się z prędkością u przyłożymy siłę i rozpędzimy ją do prędkości v, to praca potrzebna do rozpędzenia jej wyniesie 1 2 m v 2 – 1 2 m u 2 ).

Ciekawie jest spróbować powtórzyć to ćwiczenie dla cząstek poruszających się z prędkością bardzo bliską prędkości światła, jak cząstki w akceleratorach wspomnianych w poprzednim paragrafie. Drugie prawo Newtona w postaci

Siła = szybkość zmiany pędu

jest nadal prawdziwe, ale w pobliżu prędkości światła prędkość zmienia się w sposób pomijalnie mały w miarę działania siły – zamiast tego rośnie masa! Dlatego możemy napisać w doskonałym przybliżeniu,

Siła = (szybkość zmiany masy) x c

gdzie jak zwykle c jest prędkością światła. Aby być bardziej szczegółowym, załóżmy, że mamy stałą siłę F popychającą cząstkę. W pewnej chwili cząstka ma masę M i prędkość bardzo bliską c. Sekundę później, ponieważ siła nadal działa na cząstkę, a tym samym zwiększa jej pęd zgodnie z drugim prawem Newtona, cząstka będzie miała masę M+m powiedzmy, gdzie m jest wzrostem masy w wyniku pracy wykonanej przez siłę.

Jaki jest wzrost energii kinetycznej E cząstki podczas tego jednosekundowego okresu? Przez dokładną analogię do przypadku nierelatywistycznego opisanego powyżej, jest to po prostu praca wykonana przez siłę w tym okresie. Teraz, ponieważ masa cząstki zmienia się o m w ciągu jednej sekundy, m jest również szybkością zmiany masy. Dlatego na podstawie drugiego prawa Newtona w postaci

Siła = (szybkość zmiany masy) x c,

możemy napisać

Siła =mc.

Przyrost energii kinetycznej E w ciągu jednej sekundy jest tylko pracą wykonaną przez siłę,

E= siła x odległość.

Ponieważ cząstka porusza się zasadniczo z prędkością lotu, odległość, na którą działa siła w ciągu jednej sekundy wynosi tylko c metrów, c=3× 10 8 .

Więc całkowita praca, jaką wykonuje siła w ciągu tej sekundy to siła x odległość =mc×c=m c 2 .

Więc związek między przyrostem masy cząstki elatywistycznej a jej przyrostem energii kinetycznej jest następujący:

E=m c 2 .

Energia kinetyczna i masa dla powolnych cząstek

Przypomnijmy, że aby prawa Newtona były prawdziwe we wszystkich inercyjnych układach ramowych, musieliśmy założyć wzrost masy z prędkością o współczynnik 1/ 1-( v 2 / c 2 ) . Oznacza to, że nawet wolno poruszający się obiekt ma niewielki przyrost masy, gdy się porusza!

Jak ten maleńki przyrost ma się do energii kinetycznej? Rozważmy masę M, poruszającą się z prędkością v, znacznie mniejszą niż prędkość światła. Jej energia kinetyczna E= 1 2 M v 2 , jak omówiono powyżej. Jej masa wynosi M/ 1-( v 2 / c 2 ), co możemy zapisać jako M+m. Ile to jest m ?

Ponieważ mówimy o znanych nam prędkościach, jak w przypadku samolotu odrzutowego, gdzie v/c, jest naprawdę małe, możemy użyć kilku prostych sztuczek matematycznych, aby ułatwić sobie zadanie.

Pierwsza z nich jest dobrym przybliżeniem pierwiastka kwadratowego z 1-x, gdy x jest dużo mniejsze niż jeden:

1-x ≅1- 1 2 x dla x≪1.

Możesz to łatwo sprawdzić na kalkulatorze: spróbuj x= 1 100 , znajdziesz 99 100 =0.994987… co jest bardzo bliskie 1- 1 2 1 100 =0.995 !

Następnym przybliżeniem jest

1 1-x ≅1+x dla x≪1.

To też łatwo sprawdzić: ponownie weźmy x= 1 100 : 1 1-x = 1 99 100 = 100 99 =1.01010… , a 1+x= 101 100 =1.01.

Korzystając z tych przybliżeń przy x=v/c, możemy przybliżyć 1-( v 2 / c 2 ) jako 1- 1 2 ( v 2 / c 2 ) , a następnie 1/( 1- 1 2 ( v 2 / c 2 ) ) jako 1+ 1 2 ( v 2 / c 2 ) .

To oznacza, że całkowita masa przy prędkości v

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ),

i zapisując to jako M+m, widzimy, że przyrost masy m jest równy 1 2 M v 2 / c 2 .

To oznacza, że – ponownie – przyrost masy m jest związany z energią kinetyczną E przez E=m c 2 .

W rzeczywistości, nie jest trudno pokazać, używając małego rachunku, że w całym zakresie prędkości od zera do prędkości światła, poruszająca się cząstka doświadcza przyrostu masy związanego z jej energią kinetyczną przez E=m c 2 . Aby zrozumieć, dlaczego nie zauważamy tego w codziennym życiu, spróbujmy posłużyć się przykładem samolotu odrzutowego ważącego 100 ton, poruszającego się z prędkością 2000 mil na godzinę. 100 ton to 100 000 kilogramów, 2 000 mil na godzinę to około 1 000 metrów na sekundę. To jest energia akinetyczna 1 2 M v 2 o wartości ½ ×1011 dżuli, ale odpowiadająca jej zmiana masy samolotu o czynnik c 2 , 9× 10 16 , co daje rzeczywisty wzrost masy o około pół miligrama, niezbyt łatwy do wykrycia!

E = mc2

Widzieliśmy powyżej, że kiedy siła wykonuje pracę przyspieszając ciało, aby nadać mu energię kinetyczną, masa ciała wzrasta o ilość równą całkowitej pracy wykonanej przez siłę, przekazanej energii E, podzielonej przez c 2 . A co z sytuacją, gdy siła wykonuje pracę na ciele, które nie przyspiesza go, więc nie ma wzrostu energii kinetycznej? Na przykład, co jeśli po prostu podnoszę coś w stałym tempie, nadając temu ciału energię potencjalną? Okazuje się, że i w tym przypadku następuje przyrost masy określony przez E=m c 2 , oczywiście niezmiernie mały dla przedmiotów codziennego użytku.

Jednakże jest to efekt mierzalny i ważny w fizyce jądrowej. Na przykład, atom helu ma jądro, które ma dwa protony i dwa neutrony związane razem verytightly przez silną siłę przyciągania jądrowego. Jeśli przyłożona zostanie odpowiednia siła zewnętrzna, jądro to może zostać rozdzielone na dwa jądra „ciężkiego wodoru”, z których każde ma jeden proton i jeden neutron. Aby osiągnąć to rozdzielenie, trzeba wydatkować dużo energii z zewnątrz i okazuje się, że całkowita masa dwóch ciężkich jąder wodoru jest mierzalnie (około pół procenta) cięższa od pierwotnego jądra helu. Ta dodatkowa masa, pomnożona przez c 2 , jest równa energii potrzebnej do rozszczepienia jądra helu na dwie części. Co ważniejsze, energię tę można odzyskać, pozwalając dwóm ciężkim jądrom wodoru zderzyć się i połączyć, aby ponownie utworzyć jądro helu. (Oba jądra są naładowane elektrycznie dodatnio, więc odpychają się od siebie i muszą się dość szybko zbliżyć, aby pokonać to odpychanie i zbliżyć się do siebie, co spowoduje zadziałanie znacznie silniejszego przyciągania jądrowego). To jest podstawowe źródło energii dla bomby wodorowej i dla Słońca.

Okazuje się, że wszystkie formy energii, kinetyczna i różne rodzaje energii potencjalnej, mają związaną z nimi masę określoną przez E=m c 2 . W przypadku reakcji jądrowych zmiana masy jest zazwyczaj rzędu jednej tysięcznej całkowitej masy i jest łatwo mierzalna. W przypadku reakcji chemicznych zmiana masy jest rzędu miliardowej części całkowitej masy i nie jest obecnie mierzalna.

poprzedni indeks