Multiplicação de Grupos
Agora vamos investigar o que acontece quando aplicamos duas operações de simetria em sequência. Como exemplo, considere a molécula \\i(NH_3), que pertence ao grupo de pontos \i(C_{3v}}). Considere o que acontece se aplicarmos uma rotação seguida de um reflexo de sigma (C_3). Escrevemos esta operação combinada (quando escrita, as operações de simetria operam na coisa diretamente à sua direita, assim como os operadores fazem na mecânica quântica – temos que trabalhar de trás para frente da direita para a esquerda da notação para obter a ordem correta na qual os operadores são aplicados). Como veremos brevemente, a ordem em que as operações são aplicadas é importante.
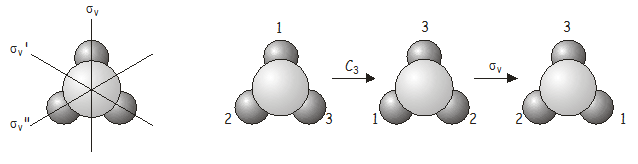
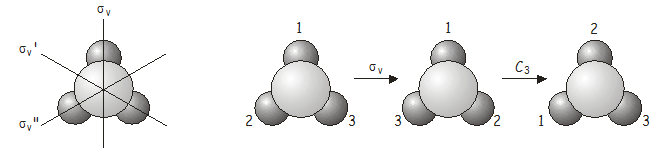
Again, a operação combinada \(C_3\)\(\sigma_v) é equivalente a outra operação do grupo de pontos, desta vez
Existem dois pontos importantes que são ilustrados por este exemplo:
Os efeitos da aplicação de duas operações de simetria em sequência dentro de um determinado grupo de pontos estão resumidos em tabelas de multiplicação de grupos. Como exemplo, a tabela de multiplicação de grupo completa para \(C_{3v}}} usando as operações de simetria como definidas nas figuras acima é mostrada abaixo. As operações escritas ao longo da primeira linha da tabela são realizadas primeiro, seguidas pelas escritas na primeira coluna (note que a tabela mudaria se escolhêssemos o nome \i1> (\i1>sigma_v), \i>sigma_v’^) e \i>sigma_v”^) em alguma ordem diferente).