Alai

Michael Fowler,UVa Physics.

Momentum tem Direção

Como discutimos na última palestra, mesmo antes de Newton formular seus estatutos, Descartes, com uma pequena ajuda de Huygens, tinha descoberto uma verdade profunda: em qualquer colisão, ou de fato, em qualquer interação de qualquer tipo, a quantidade total de “momentum” – uma medida de movimento – sempre permaneceu a mesma. O momentum de um objeto em movimento é definido como o produto da massa e da velocidade, assim como um vetor: ele tem magnitude e direção. Se você está de pé em patins sem fricção e atira uma bola, você se move para trás: você tem um momento igual em magnitude, mas indirecto oposto ao da bola, então o momento total (seu mais o da bola) permanece zero. Os foguetes funcionam da mesma forma, atirando material para fora em alta velocidade. Eles não funcionam “empurrando contra o ar”, eles trabalham contra o material que estão empurrando para fora, assim como você empurra contra uma bola que está jogando, e isso te empurra para trás, causando sua aceleração.

Se você ainda suspeita que realmente os foguetes empurram contra o ar, lembre-se que eles funcionam tão bem no espaço! Na verdade, era amplamente acreditado quando o Goddard, um americano primitivo (o Centro de Vôo Espacial Goddard tem o nome dele) falou sobre os foguetes no espaço, ele estava perdendo seu tempo. Para citar um editorial do New York Times, escrito em 1921: “O Professor Goddard não sabe a relação entre acção e reacção e a necessidade de ter algo melhor do que um vácuo contra o qual reagir. Ele parece não ter o conhecimento básico carregado diariamente nas nossas escolas secundárias”. Obviamente, os redactores do New York Times não têm os conhecimentos básicos que estão a ser aprendidos neste curso!

Na verdade, como discutimos, a conservação do momento na acollisão decorre das leis de Newton. No entanto, é um conceito mais geral, mais simples – não depende de forma alguma dos detalhes das interacções, etc. Esta simplicidade evidentemente se aplica a Einstein, que estava convencido de que quando a dinâmica foi reformulada para incluir as novas idéias sobre tempo e espaço, a conservação do momento deve se manter em qualquer quadro de inércia. Isto levou-o a algumas conclusões surpreendentes, como veremos.

Conservação do Momento na mesa de bilhar

Como um exercício de aquecimento, consideremos a conservação do momento para uma colisão de duas bolas numa mesa de bilhar. Nós desenhamos uma linha de giz no meio da mesa de bilhar, e atiramos as bolas perto, mas em lados opostos da linha de giz de cada extremidade, à mesma velocidade, de modo que elas vão bater no meio com um golpe de relance, o que vai girar suas velocidades através de um pequeno ângulo. Em outras palavras, se inicialmente dissermos que suas velocidades (igual magnitude, direção oposta) foram paralelas à direção x – a linha do giz – então, após a colisão, elas também terão pequenas velocidades iguais e opostas na direção y (as velocidades na direção x terão diminuído muito ligeiramente).

Uma Colisão Simétrica de Nave Espacial

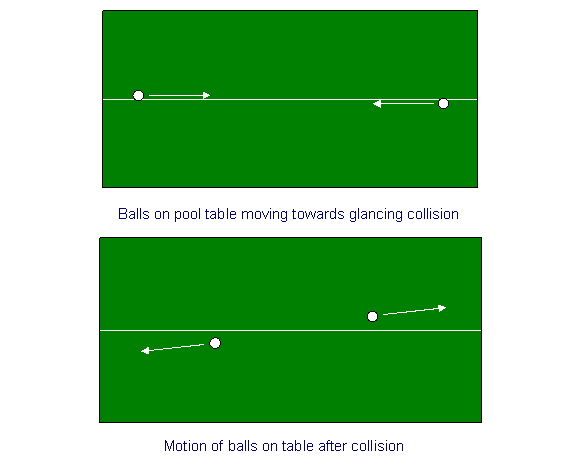
Agora vamos repetir o exercício em grande escala. Suponha que em algum lugar no espaço, longe de qualquer campo gravitacional, nós estabelecemos um cordão com um milhão de milhas de comprimento. (Pode ser entre os nossos dois relógios na experiência de dilatação temporal). Esta corda corresponde à linha de giz na mesa de bilhar. Suponha que agora temos duas naves espaciais idênticas se aproximando uma da outra com velocidades iguais e opostas paralelas à corda a partir das duas extremidades da corda, visando que elas sofram uma ligeira colisão quando se encontram no meio. É evidente pela simetria da situação que o impulso é conservado em ambas as direcções. Em particular, a velocidade a que uma nave espacial se afasta da corda após a colisão – sua velocidade y – é igual e oposta à velocidade a que a outra se afasta da corda.

Mas agora considere esta colisão como observada por alguém em uma das naves espaciais, chame-a de A. Antes da colisão, ele vê a corda se movendo muito rápido pela janela,digamos a alguns metros de distância. Após a colisão, ele vê a corda se afastando, digamos, a 15 metros de perseguição. Isto é porque a nave espacial A apanhou uma velocidade perpendicular ao cordão de 15 metros de perseguição. Entretanto, como esta é uma situação completamente simétrica, um observador na nave B deduziu que sua nave se afastava do cordel a 15 metros de persecondos também.

Apenas quão simétrico é?

A questão crucial é: a que velocidade um observador inspira a nave A a ver a nave B a afastar-se do cordel? Suponhamos que em relação à nave A, a nave B está a afastar-se (no sentido X) a 0,6c. Primeiro, lembre-se que as distâncias perpendiculares à direção do movimento não são Lorentz contraídas. Portanto, quando o observador na espaçonave B diz que se afastou 15 metros da corda em um segundointervalo, o observador observando este movimento da espaçonave A vai concordar nos 15 metros – mas vai concordar no segundo! Ele dirá que seus relógios correm devagar, de modo que, medido pelos seus relógios, 1,25 segundos se desviarão enquanto ela se move 15 metros na direção y.

Segue-se que, como resultado da dilatação do tempo, esta colisão, tal como vista a partir da nave A, não causa velocidades iguais eopositivas para as duas naves na direcção y. Inicialmente, ambas as naves estavam se movendo paralelamente ao eixo x, havia zeromentum na direção y. Sohow, podemos argumentar que há zero momento total na direcção y após a colisão, quando as naves espaciais idênticas não têm velocidades iguais eopositivas?

Einstein resgata o momento de conservação

Einstein estava tão certo de que a conservação do momento deve sempre ser evitada que o resgatou com uma hipótese ousada: a massa de um objecto deve depender da sua velocidade! Na verdade, a massa deve aumentar com a velocidade de tal forma que anule a menor velocidade y-directionvelocity resultante da dilatação do tempo. Ou seja, se um objeto em repouso tem uma massa m, movendo-se a uma velocidade v ele terá inércia correspondente a uma “massa relativista” m rel =m/ 1-( v 2 / c 2 ) . Então o momento torna-se

p → = m rel v → =m v → / 1-( v 2 / c 2 ) .

Notem que este aumento de massa relativista é um efeito indetectável a velocidades normais, mas à medida que um objecto se aproxima da velocidade de voo, a massa aumenta sem limite!

Mass Really Does Really Increase with Speed

Decidir que as massas de objetos devem depender da velocidade parece ser um preço pesado a pagar para resgatar a conservação do momento! No entanto, é uma previsão que não é difícil de verificar por experiência. A primeira confirmação veio em 1908, desviando elétrons rápidos em um tubo de vácuo. De fato, os elétrons em um tubo colorTV de estilo antigo têm cerca de meio por cento a mais de inércia que os elétrons em repouso, e isto deve ser permitido no cálculo dos campos magnéticos usados para guiá-los para a tela.

Muito mais dramaticamente, em aceleradores de partículas modernos são usados campos elétricos muito poderosos para acelerar elétrons, prótons e outras partículas. Na prática, estas partículas necessitam de forças cada vez maiores para uma maior aceleração à medida que a velocidade da luz se aproxima. Consequentemente, a velocidade da luz é um limite natural de velocidade absoluta. As partículas são aceleradas a velocidades em que a sua massa relativista é milhares de vezes maior do que a sua massa medida em repouso, normalmente chamada de “massa em repouso”.

…Ou Does It?

Actually, existe um debate contínuo entre os físicos sobre este conceito de massa relativista. O debate é em grande parte semântico: ninguém duvida que a correctexpressão para o impulso de uma partícula com uma massa de repouso m em movimento com velocidade v → é p → = m 1- v 2 / c 2 v → . Mas especialmente os físicos de partículas, muitos dos quais passam suas vidas medindo massas de repouso de partículas com grande precisão, não estão interessados em escrever isso como p → = m rel v → . Eles não gostam da ideia de uma massa variável. Por um lado, ela pode dar a impressão de que ao acelerar um balão de partículas em tamanho, ou pelo menos a sua estrutura interna de alguma forma se altera. Na verdade, uma partícula relativista apenas sofre uma contracção de Lorentz ao longo da direcção do movimento, como qualquer outra coisa. Ela vai de uma forma esférica para uma forma disclike tendo o mesmo raio transversal.

Então, como pode esta “massincrease” ser entendida? Como sempre, Einstein tinha razão: ele observou que toda forma de energia possui inércia. A própria energia cinética tem inércia. Agora a “inércia” é uma propriedade definidora da massa. A outra propriedade fundamental da massa é que ela atrai gravitacionalmente. Será que esta energia cinética faz isso? Para ver a resposta, considere uma esfera cheia de gás. Ela irá gerar um campo gravitacional esférico simétrico fora de si mesma, de força proporcional à massa total. Se aquecermos agora o gás, as partículas de gás terão essa massa aumentada (relativista), correspondente ao seu aumento de cinética energética, e o campo gravitacional externo terá aumentado proporcionalmente. (Ninguém duvida disso.)

Então a “massa relativista” tem de facto as duas propriedades básicas da massa: a inércia e a atracção gravitacional. (Como ficará claro nas próximas palestras, esta massa relativista não é nada mais que a energia total, com a própria massa em repouso agora vista como energia.)

A um nível mais trivial, alguns professores se opõem à introdução da massa relativista porque temem que os alunos assumam que a energia cinética de uma partícula em movimento relativista é apenas 1 2 m v → 2 usando a massa relativista – não é, como veremos em breve.

Footnote: Para qualquer um que possa ir um dia para um tratamento mormatematicamente sofisticado, deve ser acrescentado que a massa de descanso desempenha um papel importante como aninvariante ao passar de um quadro de referência para outro, mas a “massa relativista” usada aqui é realmente apenas o primeiro componente (a energia) do vector energia-momento dimensional de uma partícula, e por isso não é invariante.

Energia cinética e massa para partículas muito rápidas

Vamos pensar na energia cinética de uma destas partículas que viaja próximo da velocidade da luz. Recordemos que numa palestra anterior encontramos a energia cinética de uma massa m comum não-relativista (ou seja, em movimento lento) era de 1 2 m v 2 . A forma como o fizemos foi considerando o trabalho que tivemos de fazer para elevá-la através de uma certa altura: tivemos de exercer acima o mesmo peso W para elevá-la através da altura h, o trabalho total feito, ou energia gasta, sendo força x distância, Wh. Ao cair, a força da gravidade, W, fez uma quantidade exatamente igual de trabalho Wh sobre o objeto em queda, mas desta vez o trabalho foi para acelerar o objeto, para dar-lhe energia cinética. Como sabemos a velocidade de recolha dos objectos em queda, pudemos concluir que a energia cinética era de 1 2 m v 2 . (Para detalhes, veja a palestra anterior.)

Mais geralmente, poderíamos ter acelerado a massa com qualquer força F, e encontramos o trabalho feito pela força (força xdistância) para levá-la à velocidade v a partir de um arranque em pé. A energia cinética da massa, E= 1 2 m v 2 , é exactamente igual ao trabalho feito pela força de elevação da massa até essa velocidade. (Pode ser mostrado de forma semelhante que se for aplicada uma força a partícula já em movimento à velocidade u, digamos, e for acelerada até à velocidade v, o trabalho necessário é de 1 2 m v 2 – 1 2 m u 2 .)

É interessante tentar repetir o exercício para partícula em movimento muito próximo da velocidade da luz, como as partículas nos aceleradores mencionados no parágrafo anterior. A Segunda Lei de Newton, na forma

Force = taxa de mudança de momento

ainda é verdade, mas perto da velocidade da luz as mudanças de velocidade são insignificantes à medida que a força continua a funcionar – em vez disso, a massa aumenta! Portanto, wecan escrever para uma excelente aproximação,

Force = (taxa de mudança de massa) x c

onde como de costume c é a velocidade da luz. Para ser mais específico, suponha que temos uma força constante F empurrando uma partícula. Em algum instante, a partícula tem massa M, e velocidade extremamente próxima de c. Um segundo depois, como a força continua a trabalhar sobre a partícula, e assim aumenta seu impulso a partir da Segunda Lei de Newton, a partícula terá massa M+m, digamos, onde m é o aumento de massa como resultado do trabalho feito pela força.

Qual é o aumento da energia cinética E da partícula durante esse período de um segundo? Por analogia exacta com o caso então em análise acima, é apenas o trabalho feito pelo forçamento desse período. Agora, como o maciço da partícula muda por m em um segundo, m é também a taxa de mudança de massa. Portanto, da Segunda Lei de Newton na forma

Force = (taxa de mudança de massa) x c,

podemos escrever

Force =mc.

O aumento da energia cinética E no período de um segundo é apenas o trabalho feito pela força,

E= força x distância.

Desde que a partícula se move essencialmente à velocidade de voo, a distância que a força actua no período de um segundo é apenas c metros, c=3× 10 8 .

Então o trabalho total que a força faz nesse segundo é força xdistance =mc×c=m c 2 .

Hence a relação entre o aumento de massa da partícula terelativista e o seu aumento de energia cinética é:

E=m c 2 .

Energia Cinética e Massa para Partículas Lentas

Recordar que para que as Leis de Newton sejam verdadeiras em todos os quadros de inércia, tivemos de assumir um aumento de massa com velocidade pelo factor 1/ 1-( v 2 / c 2 ) . Isto implica que mesmo um objecto de movimento lento é um pequeno aumento de massa quando se move!

Como é que esse pequeno aumento se relaciona com a cinéticaenergética? Considere uma massa M, movendo-se a velocidade v, muchless do que a velocidade da luz. A sua energia cinética E= 1 2 M v 2 , como discutido acima. A sua massa é M/ 1-( v 2 / c 2 ) , que podemos escrever como M+m. O que é m ?

Desde que estamos a falar de velocidades que conhecemos, como um avião a jacto, onde o v/c, é realmente pequeno, podemos usar alguns truques matemáticos simples para tornar as coisas mais fáceis.

O primeiro é uma boa aproximação para a raiz quadrada de 1-x quando x é muito menor que um:

1-x ≅1- 1 2 x para x≪1.

Pode facilmente verificar isto com a sua calculadora: tente x= 1 100 , você encontra 99 100 =0.994987… que é extremamente próximo de 1- 1 2 1 100 =0.995 !

A próxima aproximação é

1 1-x ≅1+x para x≪1.

Esta também é fácil de verificar: novamente tome x= 1 100 : 1 1-x = 1 99 100 = 100 99 =1.01010… ,e 1+x= 101 100 =1.01.

Usando estas aproximações com x=v/c, podemos aproximar 1-( v 2 / c 2 ) como 1- 1 2 ( v 2 / c 2 ), e depois 1/( 1- 1 2 ( v 2 / c 2 ) ) como 1+ 1 2 ( v 2 / c 2 ) .

>

Esta significa a massa total à velocidade v

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ),

e escrevendo isto como M+m, vemos o aumento de massa m igual a 1 2 M v 2 / c 2 .

>

Este facto significa que – novamente – o aumento de massa m está relacionado com a energia cinética E por E=m c 2 .

Na verdade, não é difícil mostrar, usando um littlecalculus, que em toda a faixa de velocidade de zero a tão perto quanto você gosta da velocidade da luz, uma partícula em movimento experimenta um aumento de massa relacionado à sua energia cinética por E=m c 2 . Tente um exemplo, como por exemplo um avião ajet com 100 toneladas em movimento a 2.000mph. 100 toneladas são 100.000 quilos, 2.000mph isabout cerca de 1.000 metros por segundo. Isso é energia akinetic 1 2 M v 2 de ½ ×1011joules, mas a mudança de massa correspondente do avião para baixo pelo fator c 2 , 9× 10 16 , dando um aumento de massa real de cerca de meio miligrama, não muito fácil de detectar!

E = mc2

Vimos acima que quando uma força trabalha acelerando o corpo para dar-lhe energia cinética, a massa do corpo aumenta por uma quantidade igual ao trabalho total feito pela força, a energia E transferida, dividida por c 2 . E quando uma força trabalha num corpo que não está acelerando, então não há aumento da energia cinética? Por exemplo, e se eu simplesmente levantar algo a um ritmo constante, dando-lhe energia potencial? Acontece que, neste caso também, há um aumento de massa dado por E=m c 2 , claro que não é tão pequeno para os objectos do dia-a-dia.

No entanto, este é um efeito mensurável e importante da física inuclear. Por exemplo, a hélioatom tem um núcleo que tem dois prótons e dois nêutrons muito unidos por uma forte força de atração nuclear. Se for aplicada força externa suficiente, esta pode ser separada em dois núcleos de “hidrogénio pesado”, cada um dos quais tem um próton e um neutron. Muita energia externa tem que ser gasta para conseguir esta separação, e verifica-se que a massa total dos dois núcleos de hidrogênio pesado é mensurável (cerca de meio por cento) mais pesada do que o núcleo de hélio original. Esta extramassa, multiplicada por c 2 , é apenas igual à energia necessária para dividir o núcleo de hélio em dois. Ainda mais importante, esta energia pode ser recuperada deixando os dois hidrogênio-núcleos pesados colidirem e se unirem para formar novamente um núcleo de hélio. (Ambos têm carga elétrica positiva, por isso se repelem mutuamente e devem se unir bastante rápido para superar essa repulsão e chegar à proximidade onde a atração nuclear muito mais forte entra). Esta é a fonte de energia básica da bomba de hidrogénio, e do sol.

Acontece que todas as formas de energia, cinéticas e diferentes tipos de energia potencial, têm associada massa dada por E=m c 2 . Para reações nucleares, a mudança de massa é tipicamente da ordem de um milésimo da massa total, e prontamente mensurável. Para as reacções químicas, a alteração é da ordem de um bilionésimo da massa total, e não é actualmente mensurável.

index anterior