A seguinte definição de estatísticas robustas vem do livro de P. J. Huber Estatísticas Robustas.
… qualquer procedimento estatístico deve possuir as seguintes características desejáveis:
- Deve ter uma eficiência razoavelmente boa (óptima ou quase óptima) no modelo assumido.
- Deve ser robusto no sentido em que pequenos desvios das suposições do modelo devem prejudicar o desempenho apenas ligeiramente. …
- Um pouco maiores desvios do modelo não devem causar uma catástrofe.
As estatísticas clássicas se concentram no primeiro dos pontos de Huber, produzindo métodos que são ótimos sujeitos a alguns critérios. Este post analisa os exemplos canônicos usados para ilustrar o segundo e terceiro pontos de Huber.
O terceiro ponto de Huber é tipicamente ilustrado pela média da amostra (média) e a mediana da amostra (valor médio). Você pode definir quase metade dos dados de uma amostra para ∞ sem fazer com que a mediana da amostra se torne infinita. A média da amostra, por outro lado, torna-se infinita se qualquer valor da amostra for infinito. Grandes desvios do modelo, ou seja, alguns outliers, podem causar uma catástrofe para a média da amostra mas não para a mediana da amostra.
O exemplo canônico ao discutir o segundo ponto de Huber remonta a John Tukey. Comece com o exemplo mais simples de estimativa: dados de uma distribuição normal com média e variância 1 desconhecidas, ou seja, os dados são normais(μ, 1) com μ desconhecido. A maneira mais eficiente de estimar μ é pegar a média amostral, a média dos dados.
Mas agora suponha que a distribuição de dados não é exatamente normal(μ, 1), mas é uma mistura de uma distribuição normal padrão e uma distribuição normal com uma variância diferente. Que δ seja um número pequeno, digamos 0,01, e assuma que os dados vêm de uma distribuição normal(μ, 1) com probabilidade 1-δ e os dados vêm de uma distribuição normal(μ, σ2) com probabilidade δ. Essa distribuição é chamada de “normal contaminada” e o número δ é a quantidade de contaminação. A razão para usar o modelo normal contaminado é que é uma distribuição não-normal que pode parecer normal aos olhos.
Podemos estimar a média da população μ usando ou a média da amostra ou a mediana da amostra. Se os dados fossem estritamente normais e não uma mistura, a média amostral seria o estimador mais eficiente do μ. Nesse caso, o erro padrão seria cerca de 25% maior se utilizássemos a mediana da amostra. Mas se os dados forem provenientes de uma mistura, a mediana da amostra pode ser mais eficiente, dependendo dos tamanhos de δ e σ. Aqui está um gráfico da ERA (eficiência relativa assimptótica) da mediana da amostra em relação à média da amostra em função de σ quando δ = 0.01,
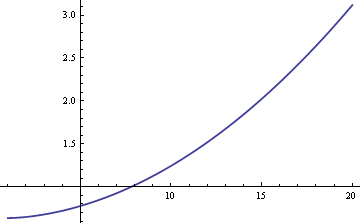
O gráfico mostra que para valores de σ maiores que 8, a mediana da amostra é mais eficiente do que a média amostral. A superioridade relativa da mediana cresce sem limite conforme aumenta σ.
Aqui está um gráfico da ARE com σ fixado em 10 e δ variando entre 0 e 1,
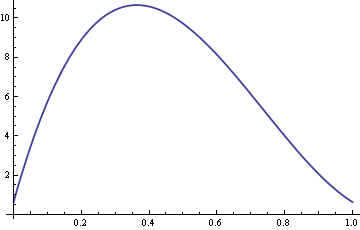
Então para valores de δ em torno de 0.4, a mediana da amostra é mais de dez vezes mais eficiente do que a média da amostra.
A fórmula geral para o ARE neste exemplo é 2((1 + δ(σ2 – 1)(1 – δ + π/σ)2)/ π.
Se você tem certeza de que seus dados são normais sem contaminação ou com muito pouca contaminação, então a média da amostra é o estimador mais eficiente. Mas pode valer a pena correr o risco de desistir de um pouco de eficiência em troca de saber que você se sairá melhor com um modelo robusto se houver contaminação significativa. Há mais potencial de perda usando a média amostral quando há contaminação significativa do que há ganho potencial usando a média amostral quando não há contaminação.
Aqui está um enigma associado com o exemplo normal contaminado. O estimador mais eficiente para os dados normais (μ, 1) é a média amostral. E o estimador mais eficiente para os dados normais (μ, σ2) também é a média da amostra. Então por que não é ótimo pegar a média amostral da mistura?
A chave é que não sabemos se uma determinada amostra veio da distribuição normal(μ, 1) ou da distribuição normal(μ, σ2). Se soubéssemos, poderíamos segregar as amostras, fazer a média separadamente e combinar as amostras em uma média agregada: multiplicando uma média por 1-δ, multiplicando a outra por δ, e adicionar. Mas como não sabemos qual dos componentes da mistura leva a quais amostras, não podemos pesar as amostras adequadamente. (Provavelmente também não sabemos δ, mas essa é uma questão diferente.)
Existem outras opções além de usar a média ou a mediana da amostra. Por exemplo, a média aparada deita fora alguns dos maiores e menores valores e depois calcula a média de tudo o resto. (Às vezes o desporto funciona desta forma, expulsando as notas mais altas e mais baixas de um atleta dos juízes). Quanto mais dados são jogados fora em cada ponta, mais a média aparada age como a mediana da amostra. Quanto menos dados jogados fora, mais ela age como a média da amostra.
Posto relacionado: Eficiência da mediana versus média para distribuições Student-t
Para dicas diárias sobre ciência de dados, siga @DataSciFact no Twitter.