Înmulțirea grupurilor
Acum vom investiga ce se întâmplă când aplicăm două operații de simetrie în succesiune. Ca exemplu, considerăm molecula \(NH_3\), care aparține grupului de puncte \(C_{3v}\). Să analizăm ce se întâmplă dacă aplicăm o rotație \(C_3\} urmată de o reflexie \(\sigma_v\). Scriem această operație combinată \(\sigma_v\)\(C_3\) (atunci când sunt scrise, operațiile de simetrie operează asupra lucrului aflat direct în dreapta lor, la fel ca operatorii în mecanica cuantică – prin urmare, trebuie să lucrăm invers, de la dreapta la stânga, din notație pentru a obține ordinea corectă în care sunt aplicați operatorii). După cum vom vedea în curând, ordinea în care sunt aplicate operațiile este importantă.
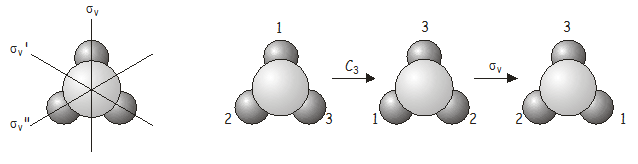
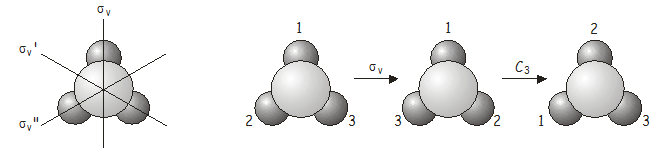
Din nou, operația combinată \(C_3\)\(\sigma_v\) este echivalentă cu o altă operație a grupului de puncte, de data aceasta \(\sigma_v’\).
Există două puncte importante care sunt ilustrate de acest exemplu:
Efectele aplicării succesive a două operații de simetrie în cadrul unui anumit grup de puncte sunt rezumate în tabelele de înmulțire a grupurilor. Ca exemplu, tabelul complet de multiplicare de grup pentru \(C_{3v}\) folosind operațiile de simetrie definite în figurile de mai sus este prezentat mai jos. Operațiile scrise de-a lungul primului rând al tabelului sunt efectuate mai întâi, urmate de cele scrise în prima coloană (rețineți că tabelul s-ar schimba dacă am alege să numim \(\sigma_v\), \(\sigma_v’\) și \(\sigma_v”\) într-o ordine diferită).
.