Alai

Michael Fowler,UVa Physics.

Momentul are Direcția

După cum am discutat în ultima prelegere, chiar înainte ca Newton să-și formuleze legile, Descartes, cu puțin ajutor din partea lui Huygens, descoperise un adevăr dinamic profund: în orice coliziune sau, de fapt, în orice interacțiune de orice fel, cantitatea totală de „momentum” – o măsură a mișcării – a rămas întotdeauna aceeași. Momentul unui obiect în mișcare este definit ca fiind produsul dintre masă și viteză și, prin urmare, este un vector: are mărime și direcție. Dacă stați în picioare pe patine fără fricțiune și aruncați o minge, vă deplasați înapoi: aveți un impuls egal ca mărime, dar cu direcție opusă celui al mingii, astfel încât impulsul total (al dumneavoastră plus cel al mingii) rămâne zero. Rachetele funcționează în același mod,aruncând material la mare viteză. Ele nu funcționează prin „împingerea împotriva aerului”, ci prin împingerea împotriva materialului pe care îl împing, la fel cum împingi împotriva unei mingi pe care o arunci, iar aceasta te împinge înapoi, provocând accelerația ta.

Dacă încă mai bănuiți că într-adevăr rachetele împing împotriva aerului, amintiți-vă că ele funcționează la fel de bine în spațiu! De fapt, se credea pe scară largă că atunci când Goddard, unul dintre primii rachetiști americani (Goddard Space Flight Center îi poartă numele) vorbea despre rachete în spațiu, își pierdea timpul. Citez dintr-un editorial din New York Times scris în 1921: „Profesorul Goddard nu cunoaște relația dintre acțiune și reacție și necesitatea de a avea ceva mai bun decât un vid împotriva căruia să reacționeze. Se pare că îi lipsesc cunoștințele de bază distribuite zilnic în liceele noastre.” Evident, editorialiștii de la New York Times de la acea vreme nu au luat în seamă cunoștințele de bază distribuite în cadrul acestui curs!

De fapt, așa cum am discutat, conservarea impulsului în cazul unei coliziuni rezultă din legile lui Newton. Cu toate acestea, este un concept mai general, mai simplu – nu depinde deloc de detaliile interacțiunilor, etc. Această simplitate i-a plăcut în mod evident lui Einstein, care era convins că, atunci când dinamica a fost reformulată pentru a include noile idei despre timp și spațiu, conservarea momentului ar trebui să fie în continuare valabilă în orice cadru inerțial. Acest lucru l-a condus la unele concluzii surprinzătoare, după cum vom vedea.

Conservarea momentului pe masa de biliard

Ca un exercițiu de încălzire, să luăm în considerare conservarea momentului pentru o coliziune a două bile pe o masă de biliard. Trasăm o linie de cretă pe mijlocul mesei de biliard și aruncăm bilele în apropierea liniei de cretă, dar de părți opuse ale acesteia, de la ambele capete, cu aceeași viteză, astfel încât ele se vor lovi în mijloc cu o lovitură de impact, ceea ce le va întoarce vitezele cu un unghi mic. Cu alte cuvinte, dacă inițial spunem că vitezele lor (mărime egală, direcție opusă) erau paralele cu direcția x – linia cretei – atunci, după ciocnire, ele vor avea viteze mici egale și opuse și în direcția y. (Vitezele în direcția x vor fi scăzut foarte puțin).

O coliziune simetrică a unei nave spațiale

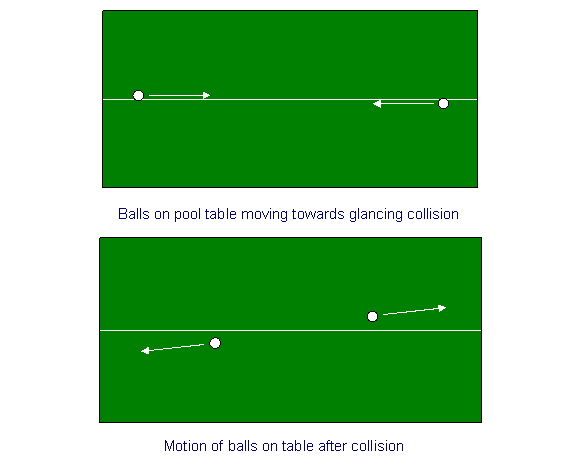
Acum să repetăm exercițiul la scară mare. Să presupunem că undeva în spațiu, departe de orice câmp gravitațional, întindem o sfoară lungă de un milion de mile. (Ar putea fi între cele două ceasuri ale noastre în experimentul de dilatare a timpului). Această sfoară corespunde liniei de cretă de pe masa de biliard. Să presupunem acum că avem două nave spațiale identice care se apropie una de cealaltă cu viteze egale și opuse, paralele cu șirul, de la cele două capete ale șirului, orientate astfel încât să sufere o coliziune ușoară când se întâlnesc la mijloc. Este evident, din simetria situației, că momentul se conservă în ambele direcții. În special, viteza cu care o navă spațială se îndepărtează de coardă după coliziune – viteza sa y – este egală și opusă vitezei cu care cealaltă se îndepărtează de coardă.

Considerăm acum această coliziune observată de cineva dintr-una dintre navele spațiale, numim-o A. Înainte de coliziune, el vede coarda mișcându-se foarte repede lângă fereastră, să zicem la câțiva metri distanță. După coliziune, el vede că șirul se îndepărtează cu, să zicem, 15 metri pe secundă. Acest lucru se datorează faptului că nava spațială A a căpătat o viteză perpendiculară pe coardă de 15 metri pe secundă. Între timp, având în vedere că această situație este complet simetrică, un observator de pe nava spațială B ar deduce cu siguranță că și nava sa se îndepărtează de coardă cu 15 metri pe secundă.

Cât de simetrică este situația?

Întrebarea crucială este: cu cât de repede vede un observator de pe nava spațială A că nava spațială B se îndepărtează de coardă? Să presupunem că în raport cu nava spațială A,nava spațială B se îndepărtează (în direcția x) cu 0,6c. În primul rând, reamintim că distanțele perpendiculare pe direcția de mișcare nu sunt contractate Lorentz. Prin urmare, atunci când observatorul din nava spațială B afirmă că s-a îndepărtat cu 15 metri de șir într-un interval de o secundă, observatorul care urmărește această mișcare de pe nava spațială A va fi de acord cu cei 15 metri – dar nu va fi de acord cu cea de o secundă! El va spune că ceasurile sale merg încet, așa că, așa cum este măsurat de ceasurile sale, 1,25 secunde se vor fi scurs în timp ce ea se deplasează 15 metri în direcția Y.

De aici rezultă că, ca urmare a dilatării timpului, această coliziune, așa cum este văzută din nava spațială A, nu determină viteze egale și opuse pentru cele două nave spațiale în direcția y. Inițial, ambele nave spațiale se deplasauparalel la axa x, exista zeromentum în direcția y. Deci, cum putem afirma că există un moment total zero în direcția y după coliziune, atunci când navele spațiale identice nu au viteze egale și opuse?

Einstein salvează conservarea momentului

Einstein era atât de sigur că conservarea momentului trebuie să se mențină întotdeauna încât a salvat-o cu o ipoteză îndrăzneață: masa unui obiect trebuie să depindă de viteza sa! De fapt, masa trebuie să crească odată cu viteza în așa fel încât să anuleze viteza mai mică pe direcția y rezultată din dilatarea timpului. Adică, dacă un obiect în repaus are masa m, în mișcare cu viteza v, el va avea o inerție corespunzătoare unei „mase relativiste” m rel =m/ 1-( v 2 / c 2 ) .Atunci momentul devine

p → = m rel v → =m v → / 1-( v 2 / c 2 ) .

Rețineți că această creștere relativistă a masei este un efect nedetectabil de mic la viteze obișnuite, dar pe măsură ce un obiect se apropie de viteza de zbor, masa crește fără limite!

Masa crește într-adevăr cu viteza

Decizia că masele obiectelor trebuie să depindă de viteză astfel pare un preț greu de plătit pentru a salva conservarea impulsului! Cu toate acestea, este o predicție care nu este greu de verificat prin experiment. Prima confirmare a venit în 1908, prin devierea electronilor rapizi într-un tub cu vid. De fapt, electronii dintr-un tub TV color de tip vechi au cu aproximativ o jumătate de procent mai multă inerție decât electronii în repaus, iar acest lucru trebuie luat în considerare la calcularea câmpurilor magnetice folosite pentru a-i ghida spre ecran.

Mult mai dramatic, în acceleratoarele moderne de particule se folosesc câmpuri electrice foarte puternice pentru a accelera electronii, protonii și alte particule. În practică s-a constatat căaceste particule au nevoie de forțe din ce în ce mai mari pentru a continua accelerarea pe măsură ce se apropie de viteza luminii. În consecință, viteza luminii este o limită naturală absolută a vitezei. Particulele sunt accelerate până la viteze la care masa lor relativistă este de mii de ori mai mare decât masa lor măsurată în repaus, numită de obicei „masa de repaus”.

…sau nu?

De fapt, există o dezbatere continuă în rândul fizicienilor cu privire la acest concept de masă relativistă. Dezbaterea este în mare parte semantică: nimeni nu se îndoiește că expresia corectă pentru momentul unei particule cu masa de repaus m care se deplasează cu viteza v → este p → = m 1- v 2 / c 2 v → . Dar fizicienii de particule în special, mulți dintre ei petrecându-și viața măsurând cu mare precizie masele de repaus ale particulelor, nu sunt încântați să scrie p → = m rel v → . Lor nu le place ideea unei mase variabile. În primul rând, aceasta ar putea da impresia că, pe măsură ce accelerează, o particulă își mărește dimensiunea sau, cel puțin, că structura sa internă se modifică cumva. De fapt, o particulă relativistă suferă doar o contracție Lorentz de-a lungul direcției de mișcare, ca orice altceva. Ea trece de la o formă sferică la o formă de disc având aceeași rază transversală.

Deci cum poate fi înțeleasă această „creștere a masei”? Ca de obicei,Einstein a avut dreptate: a remarcat că orice formă de energie posedăinerție. Energia cinetică însăși are inerție. Or, „inerția” este o proprietate definitorie a masei. Cealaltă proprietate fundamentală a masei este că ea atrage gravitațional. Oare această energie cinetică face acest lucru? Pentru a vedea răspunsul, luați în considerare o sferă umplută cu gaz. Aceasta va genera un câmp gravitațional sferic simetric în afara sa, de intensitate proporțională cu masa totală. Dacă acum încălzim gazul, particulele de gaz vor avea această masă crescută (relativistă), corespunzând energiei lor cinetice crescute, iar câmpul gravitațional extern va fi crescut proporțional. (Nimeni nu se îndoiește de aceste două aspecte.)

Deci „masa relativistă” are într-adevăr cele două proprietăți de bază ale masei: inerția și atracția gravitațională. (După cum va deveni clar în cursurile următoare, această masă relativistă nu este nimic altceva decât energia totală,masa de repaus fiind ea însăși văzută acum ca energie.)

La un nivel mai trivial, unii profesori se opun introducerii masei relativiste deoarece se tem că elevii vor presupune că energia cinetică a unei particule în mișcare relativistă este doar 1 2 m v → 2 folosind masa relativistă – nu este așa, după cum vom vedea în curând.

Nota de subsol: Pentru oricine ar putea trece cândva la un tratament mai sofisticat din punct de vedere matematic, ar trebui adăugat că masa de repaus joacă un rol important ca o invariantă la trecerea de la un cadru de referință la altul, dar „masa relativistă” folosită aici este de fapt doar prima componentă (energia) a vectorului energie-momentum cu patru dimensiuni al unei particule, și deci nu este o invariantă.

Energie cinetică și masă pentru particule foarte rapide

Să ne gândim la energia cinetică a uneia dintre aceste particule care se deplasează aproape de viteza luminii. Amintiți-vă că într-o prelegere anterioară am constatatcă energia cinetică a unei mase obișnuite nerelativiste (adică care se mișcă lent) m era 1 2 m v 2 . Am făcut acest lucru luând în considerare câtă muncă a trebuit să depunem pentru a o ridica la o anumită înălțime: a trebuit să exercităm o forță egală cu greutatea sa W pentru a o ridica la înălțimea h, munca totală depusă, sau energia consumată, fiind forța x distanța, Wh. Când a căzut înapoi, forța de gravitație, W, a efectuat o cantitate exact egală de muncă Wh asupra obiectului în cădere, dar de data aceasta munca a fost folosită pentru a accelera obiectul, pentru a-i da energie cinetică. Deoarece știm cât de repede prind viteză obiectele în cădere, am putut concluziona că energia cinetică a fost de 1 2 m v 2 . (Pentru detalii, a se vedea lecția anterioară.)

Mai general, am fi putut accelera masa cu orice forță constantă F și am fi putut afla lucrul efectuat de forță (forță xdistanță) pentru a o aduce la viteza v de la un start de pe loc. Energia cinetică a masei, E= 1 2 m v 2 , este exact egală cu lucrul efectuat de forțăpentru a aduce masa la această viteză. (Se poate demonstra în mod similar că, dacă o forță este aplicată unei particule care se deplasează deja cu viteza u, să zicem, și este accelerată până la viteza v, lucrul necesar este 1 2 m v 2 – 1 2 m u 2 . )

Este interesant să încercăm să repetăm exercițiul pentru o particulă care se mișcă foarte aproape de viteza luminii, cum ar fi particulele din acceleratoarele menționate în paragraful anterior. Legea a doua a lui Newton, sub forma

Forța = rata de schimbare a momentului

este încă adevărată, dar aproape de viteza luminii viteza se schimbă neglijabil pe măsură ce forța continuă să acționeze – în schimb, masa crește! Prin urmare, putem scrie, cu o aproximație excelentă,

Forța = (rata de schimbare a masei) x c

unde, ca de obicei, c este viteza luminii. Pentru a fi mai specifici, să presupunem că avem o forță constantă F care împinge o particulă. La un moment dat, particula are masa M și o viteză extrem de apropiată de c. O secundă mai târziu, deoarece forța continuă să lucreze asupra particulei, și astfel crește impulsul acesteia din a doua lege a lui Newton, particula va avea masa M+m să zicem, unde m este creșterea masei ca urmare a lucrului făcut de forță.

Care este creșterea energiei cinetice E a particulei în timpul acelei perioade de o secundă? Prin analogie exactă cu cazul non-relativist analizat mai sus, este doar lucrul efectuat de forța pe parcursul acelei perioade. Acum, din moment ce masa particulei se modifică cu m într-o secundă, m este, de asemenea, rata de variație a masei. Prin urmare, din a doua lege a lui Newton sub forma

Forța = (rata de variație a masei) x c,

putem scrie

Forța =mc.

Creșterea energiei cinetice E în perioada de o secundă este doar munca efectuată de forță,

E= forță x distanță.

Din moment ce particula se deplasează practic cu viteza zborului, distanța pe care acționează forța în perioada de o secundă este de doar c metri, c=3× 10 8 8 .

Atunci lucrul total pe care îl face forța în acea secundă este forță xdistanță =mc×c=m c 2 .

În consecință, relația dintre creșterea masei unei particule relativiste și creșterea energiei cinetice a acesteia este:

E=m c 2 .

Energia cinetică și masa pentru particule lente

Reamintim că, pentru ca legile lui Newton să fie valabile în toate cadrele inerțiale, a trebuit să presupunem o creștere a masei odată cu viteza cu factorul 1/ 1-( v 2 / c 2 ) . Acest lucru implică faptul că până și un obiect care se mișcă încet are o mică creștere a masei atunci când se mișcă!

Cum se raportează această creștere minusculă la energia cinetică? Să considerăm o masă M, care se mișcă cu viteza v, mult mai mică decât viteza luminii. Energia sa cinetică E= 1 2 M v 2 , așa cum am discutat mai sus. Masa sa este M/ 1-( v 2 / c 2 ), pe care o putem scrie ca M+m. Ce este m?

Din moment ce vorbim despre viteze cu care suntem familiarizați, cum ar fi un avion cu reacție, unde v/c, este foarte mic, putem folosi câteva trucuri matematice simple pentru a ușura lucrurile.

Primul dintre ele este o bună aproximare pentru rădăcina pătrată a lui 1-x atunci când x este mult mai mic decât unu:

1-x ≅1- 1 2 x pentru x≪1.

Puteți verifica cu ușurință acest lucru cu calculatorul: încercați x= 1 100 , veți găsi 99 100 =0,994987… care este extrem de aproape de 1- 1 2 1 100 =0,995 !

Următoarea aproximație este

1 1-x ≅1+x pentru x≪1.

Acest lucru este, de asemenea, ușor de verificat: luăm din nou x= 1 100 : 1 1-x = 1 99 100 = 100 99 =1,01010… ,și 1+x= 101 100 =1,01.

Utilizând aceste aproximări cu x=v/c, putem aproxima 1-( v 2 / c 2 ) ca 1- 1 1 2 ( v 2 / c 2 ) ,și apoi 1/( 1- 1 1 2 ( v 2 / c 2 ) ) ) ca 1+ 1 2 ( v 2 / c 2 ) .

Aceasta înseamnă că masa totală la viteza v

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ),

și scriind acest lucru ca M+m, vedem că creșterea masei m este egală cu 1 2 M v 2 / c 2 .

Aceasta înseamnă că – din nou – creșterea de masă m este legată de energia cinetică E prin E=m c 2 .

De fapt, nu este greu de demonstrat, folosind un pic de calcul, că pe toată gama de viteze, de la zero până la viteza luminii, o particulă în mișcare înregistrează o creștere de masă legată de energia sa cinetică prin E=m c 2 . Pentru a înțelege de ce acest lucru nu este observat în viața de zi cu zi, încercați un exemplu, cum ar fi un avion cu reacție cântărind 100 de tone care se deplasează cu 2.000 de mile pe oră. 100 de tone înseamnă 100.000 de kilograme, iar 2.000 de mile pe oră înseamnă aproximativ 1.000 de metri pe secundă. Aceasta înseamnă o energie cinetică 1 2 M v 2 de ½ ×1011jouli, dar modificarea corespunzătoare a masei avionului scade cu factorul c 2 , 9 × 10 16 , ceea ce înseamnă o creștere reală a masei de aproximativ o jumătate de miligram, nu prea ușor de detectat!

E = mc2

Am văzut mai sus că atunci când o forță lucrează accelerând un corp pentru a-i da energie cinetică, masa corpului crește cu o cantitate egală cu lucrul total efectuat de forță, energia E transferată, împărțită la c 2 . Ce se întâmplă atunci când o forță acționează asupra unui corp care nu îl accelerează, deci nu există o creștere a energiei cinetice? De exemplu, ce se întâmplă dacă ridic ceva la o viteză constantă, dându-i energie potențială? Se pare că și în acest caz există o creștere a masei dată de E=m c 2 , bineînțeles nesemnificativ de mică pentru obiectele obișnuite.

Cu toate acestea, acesta este un efect măsurabil și important în fizica nucleară. De exemplu, heliomatul are un nucleu care are doi protoni și doi neutroni legați foarte strâns între ei printr-o forță de atracție nucleară puternică. Dacă se aplică o forță exterioară suficientă, acesta poate fi separat în două nuclee de „hidrogen greu”, fiecare dintre acestea având un proton și un neutron. Pentru a realiza această separare, trebuie consumată multă energie exterioară și se constată că masa totală a celor două nuclee grele de hidrogen este cu mult mai grea (aproximativ o jumătate de procent) decât cea a nucleului de heliu inițial. Această masă suplimentară, înmulțită cu c 2 , este exact egală cu energia necesară pentru a separa nucleul de heliu în două. Chiar mai important, această energie poate fi recuperată lăsând cele două nuclee grele de hidrogen să se ciocnească și să se unească pentru a forma din nou un nucleu de heliu. (Amândouă sunt încărcate electric pozitiv,deci se resping reciproc și trebuie să se întâlnească destul de repede pentru a învinge această respingere și a ajunge la apropierea în care intră în acțiune atracția nucleară mult mai puternică). Aceasta este sursa de energie de bază a bombei cu hidrogen și a soarelui.

Se pare că toate formele de energie, cinetică și diferite tipuri de energie potențială, au masa asociată dată de E=m c 2 . În cazul reacțiilor nucleare, schimbarea de masă este, în mod obișnuit, de ordinul unei miimi din masa totală și este ușor de măsurat. Pentru reacțiile chimice, schimbarea este de ordinul unei miliardimi din masa totală și nu este în prezent măsurabilă.

index anterior

.