Următoarea definiție a statisticii robuste provine din cartea lui P. J. Huber Robust Statistics.
… orice procedură statistică ar trebui să posede următoarele caracteristici dezirabile:
- Ar trebui să aibă o eficiență rezonabil de bună (optimă sau aproape optimă) la modelul presupus.
- Ar trebui să fie robustă în sensul că abaterile mici de la ipotezele modelului ar trebui să afecteze performanța doar puțin. …
- Devierile ceva mai mari de la model nu ar trebui să provoace o catastrofă.
Statistica clasică se concentrează pe primul dintre punctele lui Huber, producând metode care sunt optime în funcție de anumite criterii. Această postare analizează exemplele canonice folosite pentru a ilustra al doilea și al treilea punct al lui Huber.
Cel de-al treilea punct al lui Huber este ilustrat în mod obișnuit de media eșantionului (media) și de mediana eșantionului (valoarea de mijloc). Puteți seta aproape jumătate din datele dintr-un eșantion la ∞ fără a face ca mediana eșantionului să devină infinită. Media eșantionului, pe de altă parte, devine infinită dacă orice valoare a eșantionului este infinită. Abaterile mari de la model, adică câteva valori aberante, ar putea provoca o catastrofă pentru media eșantionului, dar nu și pentru mediana eșantionului.
Exemplul canonic atunci când se discută al doilea punct al lui Huber se întoarce la John Tukey. Începeți cu cel mai simplu exemplu de manual de estimare: date dintr-o distribuție normală cu media necunoscută și varianța 1, adică datele sunt normale(μ, 1) cu μ necunoscut. Cel mai eficient mod de a estima μ este de a lua media eșantionului, media datelor.
Dar acum să presupunem că distribuția datelor nu este exact normală(μ, 1), ci este un amestec de distribuție normală standard și o distribuție normală cu o varianță diferită. Fie δ un număr mic, să zicem 0,01, și să presupunem că datele provin dintr-o distribuție normală(μ, 1) cu probabilitatea 1-δ și că datele provin dintr-o distribuție normală(μ, σ2) cu probabilitatea δ. Această distribuție se numește „normală contaminată”, iar numărul δ reprezintă valoarea contaminării. Motivul pentru care se folosește modelul normal contaminat este că este o distribuție non-normală care poate părea normală cu ochiul liber.
Am putea estima media populației μ folosind fie media eșantionului, fie mediana eșantionului. Dacă datele ar fi strict normale, mai degrabă decât un amestec, media eșantionului ar fi cel mai eficient estimator al lui μ. În acest caz, eroarea standard ar fi cu aproximativ 25% mai mare dacă am folosi mediana eșantionului. Dar dacă datele provin dintr-un amestec, mediana eșantionului poate fi mai eficientă, în funcție de dimensiunile lui δ și σ. Iată un grafic al ARE (eficiența relativă asimptotică) a medianei eșantionului în comparație cu media eșantionului în funcție de σ atunci când δ = 0.01.
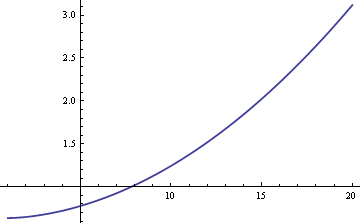
Pratgraful arată că, pentru valori ale lui σ mai mari de 8, mediana eșantionului este mai eficientă decât media eșantionului. Superioritatea relativă a medianei crește fără limite pe măsură ce σ crește.
Iată un grafic al ARE cu σ fixat la 10 și δ variind între 0 și 1.
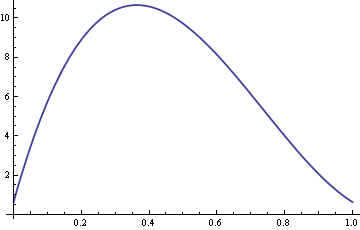
Așa că pentru valori ale lui δ în jur de 0.4, mediana eșantionului este de peste zece ori mai eficientă decât media eșantionului.
Formula generală pentru ARE în acest exemplu este 2((1 + δ(σ2 – 1)(1 – δ + δ/σ)2)/ π.
Dacă sunteți sigur că datele dvs. sunt normale, fără contaminare sau cu o contaminare foarte mică, atunci media eșantionului este cel mai eficient estimator. Dar s-ar putea să merite să riscați să renunțați la puțină eficiență în schimbul faptului că știți că vă veți descurca mai bine cu un model robust dacă există o contaminare semnificativă. Există un potențial mai mare de pierdere folosind media eșantionului atunci când există o contaminare semnificativă decât un potențial câștig folosind media eșantionului atunci când nu există contaminare.
Iată o enigmă asociată cu exemplul normal contaminat. Cel mai eficient estimator pentru datele normale(μ, 1) este media eșantionului. Iar cel mai eficient estimator pentru datele normal(μ, σ2) este, de asemenea, să se ia media eșantionului. Atunci de ce nu este optim să luăm media eșantionului amestecului?
Cheia este că nu știm dacă un anumit eșantion provine din distribuția normală(μ, 1) sau din distribuția normală(μ, σ2). Dacă am ști, am putea să separăm eșantioanele, să le calculăm media separat și să combinăm eșantioanele într-o medie agregată: înmulțind o medie cu 1-δ, înmulțind-o pe cealaltă cu δ și adăugând. Dar, din moment ce nu știm care dintre componentele amestecului conduc la ce eșantioane, nu putem cântări eșantioanele în mod corespunzător. (Probabil că nu cunoaștem nici δ, dar aceasta este o altă problemă.)
Există și alte opțiuni decât utilizarea mediei eșantionului sau a medianei eșantionului. De exemplu, media tăioasă aruncă unele dintre cele mai mari și cele mai mici valori, apoi face o medie a tuturor celorlalte. (Uneori, sporturile funcționează în acest fel, aruncând cele mai mari și cele mai mici note ale unui atlet din partea judecătorilor). Cu cât mai multe date aruncate la fiecare capăt, cu atât mai mult media ajustată se comportă ca mediana eșantionului. Cu cât mai puține date aruncate, cu atât mai mult se comportă ca media eșantionului.
Post conex: Eficiența medianei față de medie pentru distribuțiile Student-t
Pentru sfaturi zilnice despre știința datelor, urmăriți @DataSciFact pe Twitter.
.