Fysiikassa voima on kappaleiden välinen vuorovaikutus. Sitä kutsutaan vuorovaikutukseksi, koska jos yksi esine vaikuttaa toiseen, sen toimintaan vastaa toisen esineen reaktio. Tämä ajatus tunnetaan Newtonin kolmantena lakina, jossa vaikutus ja reaktio ovat ”yhtä suuret ja vastakkaiset” (matching). Esineet ovat vain asioita, joiden välillä voima vaikuttaa. Erilaiset voimat vaikuttavat erityyppisten esineiden välillä. Esimerkiksi painovoima vaikuttaa sellaisten kappaleiden välillä, joilla on massaa, kuten auringon ja maan välillä. Toinen esimerkki on sähkömagneettinen voima, joka vaikuttaa varauksellisten kohteiden, kuten elektronin ja atomin ytimen, välillä. Painovoima ja sähkömagneettinen voima ovat kaksi esimerkkiä voimista.
Voima muuttaa kappaleen tilaa (jokin fysikaalinen suure muuttuu) tai tarkkaan ottaen kahden kappaleen tilaa, koska voima on vuorovaikutusta. Voima saa esimerkiksi aikaan sen, että vaikutuksen kohteena olevaa esinettä työnnetään tai vedetään tiettyyn suuntaan. Tämä muuttaa kappaleen impulssia. Voimat saavat esineet kiihtymään, lisäävät esineen kokonaispainetta, muuttavat suuntaa tai muuttavat muotoaan. Voiman voimakkuus mitataan newtonseina (N). Fysiikassa on neljä perusvoimaa.
Voima on aina työntö, veto tai kierto, ja se vaikuttaa kohteisiin työntämällä niitä ylöspäin, vetämällä niitä alaspäin, työntämällä niitä sivulle tai muuttamalla niiden liikettä tai muotoa jollakin muulla tavalla.
Newtonin toinen laki
Newtonin toisen liikelain mukaan kaava voiman löytämiseksi on:
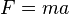
jossa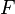 
on voima,
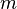esineen massa,
ja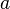 
esineen nopeus.
Tämä kaava sanoo, että kun kappaleeseen kohdistuu voima, niin se liikkuu yhä nopeammin. Jos voima on heikko ja esine on raskas, niin kestää kauan ennen kuin nopeus kasvaa kovin paljon, mutta jos voima on voimakas ja esine on kevyt, niin se liikkuu paljon nopeammin hyvin nopeasti.
Paino
Gravitaatio on kiihtyvyys. Kaikkea, jolla on massaa, vedetään kohti Maata tuon kiihtyvyyden takia. Tämä vetovoima on voima, jota kutsutaan painoksi.
Voidaan ottaa yllä oleva yhtälö ja muuttaa 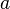standardipainovoimaksi g, jolloin saadaan kaava maapallon painovoimasta:
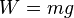
jossa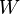 
on esineen paino,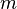esineen massa,
ja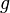 
painovoiman aiheuttama kiihtyvyys merenpinnan korkeudella. Se on noin 
.
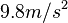Tämä kaava sanoo, että kun tiedät esineen massan, voit laskea, kuinka suuri voima esineeseen kohdistuu painovoiman takia. Sinun täytyy olla maapallolla, jotta voit käyttää tätä kaavaa. Jos olet kuussa tai toisella planeetalla, voit käyttää kaavaa, mutta g on eri.
Voima on vektori, joten se voi olla voimakkaampi tai heikompi ja se voi myös osoittaa eri suuntiin. Painovoima osoittaa aina alaspäin maahan (jos et ole avaruudessa).
Gravitaatiovoima
Toinen yhtälö, joka kertoo jotain gravitaatiosta on:
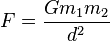
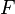on voima; 
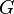on gravitaatiovakio, jota käytetään osoittamaan, miten painovoima kiihdyttää esinettä; 
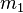on yhden kappaleen massa; 
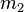on toisen kappaleen massa; ja 
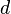on kappaleiden välinen etäisyys.
Tämän yhtälön avulla lasketaan, miten maa liikkuu auringon ympäri ja miten kuu liikkuu maan ympäri. Sitä käytetään myös laskettaessa, miten muut planeetat, tähdet ja avaruudessa olevat esineet liikkuvat.
Yhtälö kertoo, että jos kaksi esinettä on hyvin painavia, niiden välillä on voimakas voima painovoiman vuoksi. Jos ne ovat hyvin kaukana toisistaan, voima on heikompi.
- Painovoima
Kuvia lapsille
-
Aristoteles kuvasi tunnetusti voiman kaikeksi, joka saa esineen aiheuttaman ”luonnottomaan liikkeeseen”
-
Galileo Galilei oli ensimmäinen, joka huomautti Aristoteleen voimien kuvaukseen sisältyvistä ristiriitaisuuksista.
-
Kuvia vapaasti putoavasta koripallosta, jotka on otettu stroboskoopilla 20 välähdyksen sekunnissa. Oikealla olevat etäisyysyksiköt ovat noin 12 millimetrin kerrannaisia. Koripallo lähtee liikkeelle levosta. Ensimmäisen välähdyksen aikaan (etäisyys nolla) se päästetään irti, minkä jälkeen pudonneiden yksiköiden määrä on yhtä suuri kuin välähdysten lukumäärän neliö.
-
Gravityn kaltaiset laitteet tarjoavat tehokkaan luotaimen painovoiman havaitsemiseen.
-
Fk on voima, joka vastaa kuormitusta, joka kohdistuu jouselle
-
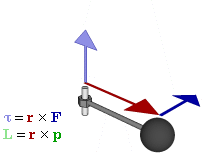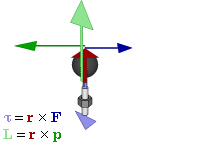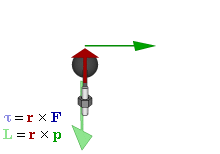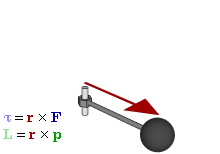
Voiman (F) välinen suhde, vääntömomentti (τ) ja momenttivektorit (p ja L) pyörivässä systeemissä.
gd:Neart