Moltiplicazione dei gruppi
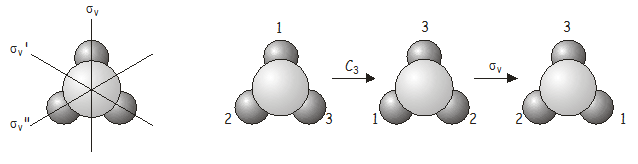
Ora studieremo cosa succede quando applichiamo due operazioni di simmetria in sequenza. Come esempio, consideriamo la molecola \(NH_3\), che appartiene al gruppo di punti \(C_{3v}). Considera cosa succede se applichiamo una rotazione \(C_3\) seguita da una riflessione \(\sigma_v\). Scriviamo questa operazione combinata \(\sigma_v\)\(C_3\) (quando si scrive, le operazioni di simmetria operano sulla cosa direttamente alla loro destra, proprio come fanno gli operatori in meccanica quantistica – dobbiamo quindi lavorare all’indietro da destra a sinistra dalla notazione per ottenere l’ordine corretto in cui gli operatori sono applicati). Come vedremo tra poco, l’ordine in cui le operazioni sono applicate è importante.
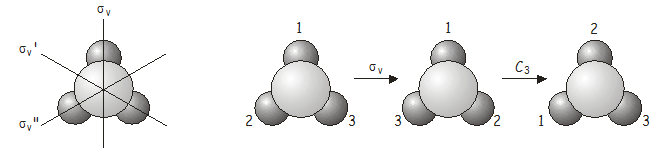
Ancora una volta, l’operazione combinata \(C_3\)\(\sigma_v\) è equivalente a un’altra operazione del gruppo di punti, questa volta \(\sigma_v’\).
Ci sono due punti importanti che sono illustrati da questo esempio:
Gli effetti dell’applicazione di due operazioni di simmetria in sequenza all’interno di un dato gruppo di punti sono riassunti nelle tabelle di moltiplicazione di gruppo. Come esempio, la tabella di moltiplicazione di gruppo completa per \(C_{3v}\) usando le operazioni di simmetria come definite nelle figure precedenti è mostrata qui sotto. Le operazioni scritte lungo la prima riga della tabella sono eseguite per prime, seguite da quelle scritte nella prima colonna (nota che la tabella cambierebbe se scegliessimo di nominare \(\sigma_v\), \(\sigma_v’\) e \(\sigma_v”\) in qualche ordine diverso).