Alai

Michael Fowler,UVa Physics.

La quantità di moto ha direzione

Come abbiamo discusso nell’ultima lezione, anche prima che Newton formulasse le sue leggi, Cartesio, con un piccolo aiuto di Huygens, aveva scoperto una profonda verità dinamica: in ogni collisione, o in effetti in ogni interazione di qualsiasi tipo, la quantità totale di “quantità di moto” – una misura del movimento – rimaneva sempre la stessa. La quantità di moto di un oggetto in movimento è definita come il prodotto della massa e della velocità, e quindi è un vettore: ha grandezza e direzione. Se sei in piedi su pattini senza attrito e lanci una palla, ti muovi all’indietro: hai una quantità di moto uguale in grandezza, ma di direzione opposta, a quella della palla, quindi la quantità di moto totale (la tua più quella della palla) rimane zero. I razzi funzionano allo stesso modo, lanciando materiale ad alta velocità. Non funzionano “spingendo contro l’aria”, funzionano spingendo contro il materiale che stanno spingendo fuori, proprio come tu spingi contro una palla che stai lanciando, e questa ti spinge indietro, causando la tua accelerazione.

Se sospetti ancora che i razzi spingano davvero contro l’aria, ricorda che funzionano altrettanto bene nello spazio! In effetti, era opinione diffusa che quando Goddard, uno dei primi rockettari americani (il Goddard Space Flight Center porta il suo nome) parlava di razzi nello spazio, stava perdendo tempo. Per citare un editoriale del New York Times scritto nel 1921: “Il professor Goddard non conosce la relazione tra azione e reazione e la necessità di avere qualcosa di meglio del vuoto contro cui reagire. Sembra che gli manchi la conoscenza di base distribuita quotidianamente nelle nostre scuole superiori”. Ovviamente, gli editoriali del New York Times dell’epoca si sono fatti sfuggire le conoscenze di base che vengono distribuite in questo corso!

In effetti, come abbiamo discusso, la conservazione della quantità di moto in una collisione deriva dalle leggi di Newton. Tuttavia, è un concetto più generale, più semplice – non dipende affatto dai dettagli delle interazioni, ecc. Questa semplicità evidentemente piacque ad Einstein, che era convinto che quando la dinamica fu riformulata per includere le nuove idee sul tempo e lo spazio, la conservazione della quantità di moto doveva ancora essere vera in qualsiasi quadro inerziale. Questo lo portò ad alcune conclusioni sorprendenti, come vedremo.

Conservazione del momento sul tavolo da biliardo

Come esercizio di riscaldamento, consideriamo la conservazione del momento per una collisione di due palle su un tavolo da biliardo. Tracciamo una linea di gesso lungo il centro del tavolo da biliardo, e spariamo le palle vicino, ma su lati opposti della linea di gesso da entrambe le estremità, alla stessa velocità, in modo che si colpiscano al centro con un colpo secco, che trasformerà le loro velocità in un piccolo angolo. In altre parole, se inizialmente diciamo che le loro velocità (uguale grandezza, direzione opposta) erano parallele alla direzione x – la linea del gesso – allora dopo la collisione avranno anche piccole velocità uguali e opposte nella direzione y. (Le velocità nella direzione x saranno diminuite molto leggermente).

Una collisione simmetrica tra astronavi

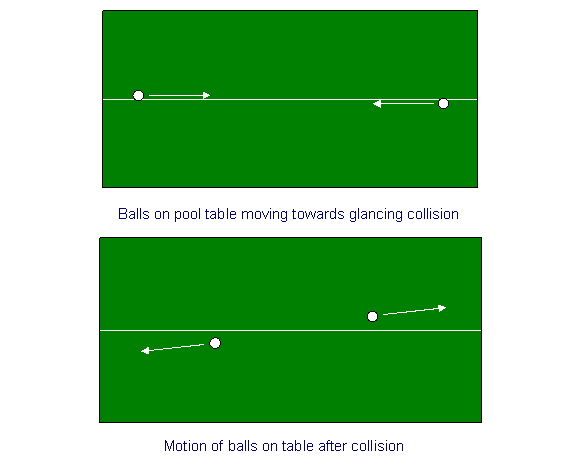
Ora ripetiamo l’esercizio su grande scala. Supponiamo che da qualche parte nello spazio, lontano da qualsiasi campo gravitazionale, si metta una corda lunga un milione di miglia. (Potrebbe essere tra i nostri due orologi nell’esperimento di dilatazione del tempo). Questa stringa corrisponde alla linea di gesso sul tavolo da biliardo. Supponiamo ora di avere due astronavi identiche che si avvicinano l’una all’altra con velocità uguali e opposte parallelamente alla corda dalle due estremità della corda, orientate in modo da subire una leggera collisione quando si incontrano nel mezzo. È evidente dalla simmetria della situazione che la quantità di moto si conserva in entrambe le direzioni. In particolare, la velocità con cui un’astronave si allontana dalla corda dopo la collisione – la sua velocità y – è uguale e opposta alla velocità con cui l’altra si allontana dalla corda.

Ma ora consideriamo questa collisione come osservata da qualcuno in una delle astronavi, chiamiamola A. Prima della collisione, egli vede la corda muoversi molto velocemente vicino alla finestra, diciamo a pochi metri di distanza. Dopo la collisione, vede la corda allontanarsi, diciamo a 15 metri al secondo. Questo perché l’astronave Ah ha preso una velocità perpendicolare alla corda di 15 metri al secondo. Nel frattempo, poiché questa è una situazione completamente simmetrica, un osservatore sull’astronave B dedurrebbe sicuramente che anche la sua astronave si sta allontanando dalla corda a 15 metri al secondo.

Quanto è simmetrico?

La domanda cruciale è: a che velocità un osservatore che ispira l’astronave A vede l’astronave B allontanarsi dalla corda? Supponiamo che rispetto all’astronave A, l’astronave B si stia allontanando (in direzione x) a 0,6c. Innanzitutto, ricordiamo che le distanze perpendicolari alla direzione del moto non sono contratte secondo Lorentz. Pertanto, quando l’osservatore nell’astronave B dice di essersi spostato di 15 metri più lontano dalla corda in un intervallo di un secondo, l’osservatore che osserva questo movimento dall’astronave A sarà d’accordo sui 15 metri – ma non sarà d’accordo sul secondo! Egli dirà che i suoi orologi vanno lenti, quindi, misurati dai suoi orologi, saranno trascorsi 1,25 secondi mentre lei si muove di 15 metri in direzione y.

Segue che, come risultato della dilatazione del tempo, questa collisione vista dall’astronave A non causa velocità uguali e opposte per le due astronavi nella direzione y. Inizialmente, entrambe le astronavi si muovevano parallelamente all’asse x, c’era zeromento nella direzione y. Quindi come possiamo sostenere che c’è zero quantità di moto totale nella direzione y dopo la collisione, quando le astronavi identiche non hanno velocità uguali e opposte?

Einstein salva la conservazione della quantità di moto

Einstein era così sicuro che la conservazione della quantità di moto dovesse essere sempre valida che la salvò con un’ipotesi audace: la massa di un oggetto deve dipendere dalla sua velocità! Infatti, la massa deve aumentare con la velocità in modo tale da annullare la minore velocità in direzione y risultante dalla dilatazione del tempo. Cioè, se un oggetto a riposo ha una massa m, muovendosi ad una velocità v avrà un’inerzia corrispondente ad una “massa relativistica” m rel =m/ 1-( v 2 / c 2 ) .Allora la quantità di moto diventa

p → = m rel v → =m v → / 1-( v 2 / c 2 ) .

Nota che questo aumento di massa relativistico è un effetto impercettibile a velocità ordinarie, ma quando un oggetto si avvicina alla velocità di volo, la massa aumenta senza limiti!

La massa aumenta davvero con la velocità

Decidere che le masse degli oggetti devono dipendere dalla velocità sembra un prezzo pesante da pagare per salvare la conservazione della quantità di moto! Tuttavia, è una previsione che non è difficile da verificare con l’esperimento. La prima conferma arrivò nel 1908, deviando gli elettroni veloci in un tubo a vuoto. Infatti, gli elettroni in un tubo colorTV vecchio stile hanno circa mezzo per cento più inerzia di elettroni a riposo, e questo deve essere consentito nel calcolo dei campi magnetici utilizzati per guidarli allo schermo.

Molto più drammaticamente, nei moderni acceleratori di particelle si usano campi elettrici molto potenti per accelerare elettroni, protoni e altre particelle. In pratica si scopre che queste particelle hanno bisogno di forze sempre maggiori per un’ulteriore accelerazione man mano che ci si avvicina alla velocità della luce. Di conseguenza, la velocità della luce è un limite assoluto naturale di velocità. Le particelle vengono accelerate a velocità in cui la loro massa relativistica è migliaia di volte maggiore della loro massa misurata a riposo, di solito chiamata “massa a riposo”.

…Oppure sì?

In realtà, c’è un continuo dibattito tra i fisici sul concetto di massa relativistica. Il dibattito è in gran parte semantico: nessuno dubita che l’espressione corretta per la quantità di moto di una particella con massa a riposo m che si muove con velocità v → sia p → = m 1- v 2 / c 2 v → . Ma soprattutto i fisici delle particelle, molti dei quali passano la vita a misurare con grande precisione le masse a riposo delle particelle, non sono entusiasti di scrivere questo come p → = m rel v → . A loro non piace l’idea di una massa variabile. Per una cosa, potrebbe dare l’impressione che mentre accelera una particella si gonfi di dimensioni, o almeno che la sua struttura interna si alteri in qualche modo. In effetti, una particella relativistica subisce solo una contrazione di Lorentz lungo la direzione del moto, come qualsiasi altra cosa. Passa da una forma sferica ad una forma a disco con lo stesso raggio trasversale.

Come si può dunque comprendere questo “aumento di massa”? Come al solito, Einstein aveva ragione: ha osservato che ogni forma di energia possiede un’inerzia. La stessa energia cinetica ha inerzia. Ora “l’inerzia” è una proprietà che definisce la massa. L’altra proprietà fondamentale della massa è che attrae gravitazionalmente. Questa energia cinetica lo fa? Per vedere la risposta, considerate una sfera riempita di gas. Essa genererà un campo gravitazionale sfericamente simmetrico al suo esterno, di forza proporzionale alla massa totale. Se ora riscaldiamo il gas, le particelle del gas avranno questa massa aumentata (relativistica), corrispondente alla loro maggiore energia cinetica, e il campo gravitazionale esterno sarà aumentato proporzionalmente. (Nessuno dubita di questo.)

Quindi la “massa relativistica” ha davvero le due proprietà fondamentali della massa: inerzia e attrazione gravitazionale. (Come diventerà chiaro nelle lezioni seguenti, questa massa relativistica non è altro che l’energia totale, con la massa a riposo stessa vista ora come energia.)

A un livello più banale, alcuni insegnanti si oppongono all’introduzione della massa relativistica perché temono che gli studenti assumano che l’energia cinetica di una particella in movimento relativistico sia solo 1 2 m v → 2 usando la massa relativistica – non lo è, come vedremo tra poco.

Nota: Per chiunque possa passare qualche volta a un trattamento più matematicamente sofisticato, si dovrebbe aggiungere che la massa a riposo gioca un ruolo importante come invariante nel passaggio da un sistema di riferimento a un altro, ma la “massa relativistica” usata qui è davvero solo la prima componente (l’energia) del vettore energia-momento di una particella di quattro dimensioni, e quindi non è un’invariante.

Energia cinetica e massa per particelle molto veloci

Pensiamo all’energia cinetica di una di queste particelle che viaggia vicino alla velocità della luce. Ricordiamo che in una lezione precedente abbiamo trovato che l’energia cinetica di una massa m ordinaria non relativistica (cioè che si muove lentamente) era 1 2 m v 2 . Il modo in cui lo abbiamo fatto è stato considerare quanto lavoro abbiamo dovuto fare per sollevarla ad una certa altezza: abbiamo dovuto esercitare una forza pari al suo peso W per sollevarla ad un’altezza h, il lavoro totale fatto, o energia spesa, essendo forza x distanza, Wh. Mentre cadeva giù, la forza di gravità, W, faceva esattamente la stessa quantità di lavoro Wh sull’oggetto che cadeva, ma questa volta il lavoro finiva per accelerare l’oggetto, per dargli energia cinetica. Poiché sappiamo quanto velocemente gli oggetti in caduta raccolgono la velocità, siamo stati in grado di concludere che l’energia cinetica era 1 2 m v 2 . (Più in generale, avremmo potuto accelerare la massa con una qualsiasi forza costante F, e trovare il lavoro fatto dalla forza (forza x distanza) per portarla alla velocità v da una partenza da fermo. L’energia cinetica della massa, E= 1 2 m v 2 , è esattamente uguale al lavoro fatto dalla forza nel portare la massa a quella velocità. (Si può dimostrare in modo simile che se una forza viene applicata ad una particella che si muove già alla velocità u, diciamo, e viene accelerata alla velocità v, il lavoro necessario è 1 2 m v 2 – 1 2 m u 2 . )

È interessante provare a ripetere l’esercizio per particelle che si muovono molto vicine alla velocità della luce, come le particelle negli acceleratori menzionati nel paragrafo precedente. La seconda legge di Newton, nella forma

Forza = tasso di variazione della quantità di moto

è ancora vera, ma vicino alla velocità della luce la velocità cambia in modo trascurabile mentre la forza continua a lavorare – invece, la massa aumenta! Quindi, possiamo scrivere con ottima approssimazione,

Forza = (tasso di variazione della massa) x c

dove come al solito c è la velocità della luce. Per essere più specifici, supponiamo di avere una forza costante F che spinge una particella. In un certo istante, la particella ha massa M, e velocità estremamente vicina a c. Un secondo dopo, poiché la forza continua a lavorare sulla particella, e quindi aumenta la sua quantità di moto per la seconda legge di Newton, la particella avrà massa M+m, dove m è l’aumento di massa come risultato del lavoro fatto dalla forza.

Qual è l’aumento dell’energia cinetica E della particella durante quel periodo di un secondo? Per esatta analogia con il caso non relativistico esaminato sopra, è solo il lavoro fatto dalla forza durante quel periodo. Ora, poiché la massa della particella cambia di m in un secondo, m è anche il tasso di cambiamento della massa. Quindi, dalla seconda legge di Newton nella forma

Forza = (tasso di cambiamento della massa) x c,

possiamo scrivere

Forza =mc.

L’aumento di energia cinetica E nel periodo di un secondo è solo il lavoro fatto dalla forza,

E= forza x distanza.

Siccome la particella si muove essenzialmente alla velocità di volo, la distanza su cui la forza agisce nel periodo di un secondo è solo c metri, c=3× 10 8 .

Quindi il lavoro totale che la forza fa in quel secondo è forza xdistanza =mc×c=m c 2 .

Quindi la relazione tra l’aumento di massa della particella elativistica e il suo aumento di energia cinetica è:

E=m c 2 .

Energia cinetica e massa per particelle lente

Ricordo che per ottenere che le leggi di Newton siano vere in tutti i sistemi inerziali, abbiamo dovuto assumere un aumento della massa con la velocità del fattore 1/ 1-( v 2 / c 2 ). Questo implica che anche un oggetto lento ha un piccolo aumento di massa quando si muove!

Come si rapporta questo piccolo aumento all’energia cinetica? Consideriamo una massa M che si muove alla velocità v, molto meno della velocità della luce. La sua energia cinetica E= 1 2 M v 2 , come discusso sopra. La sua massa è M/ 1-( v 2 / c 2 ), che possiamo scrivere come M+m. Cos’è m?

Siccome stiamo parlando di velocità che ci sono familiari, come un aereo a reazione, dove v/c, è veramente piccolo, possiamo usare alcuni semplici trucchi matematici per rendere le cose più facili.

Il primo è una buona approssimazione per la radice quadrata di 1-x quando x è molto meno di uno:

1-x ≅1- 1 2 x per x≪1.

Puoi verificarlo facilmente con la tua calcolatrice: prova x= 1 100 , trovi 99 100 =0.994987… che è estremamente vicino a 1- 1 2 1 100 =0.995 !

La prossima approssimazione è

1 1-x ≅1+x per x≪1.

Anche questo è facile da verificare: prendiamo di nuovo x= 1 100: 1 1-x = 1 99 100 = 100 99 =1.01010… ,e 1+x= 101 100 =1.01.

Utilizzando queste approssimazioni con x=v/c, possiamo approssimare 1-( v 2 / c 2 ) come 1- 1 2 ( v 2 / c 2 ), e poi 1/( 1- 1 2 ( v 2 / c 2 ) ) come 1+ 1 2 ( v 2 / c 2 ) .

Questo significa che la massa totale alla velocità v

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ),

e scrivendo questo come M+m, vediamo che l’aumento di massa m è uguale a 1 2 M v 2 / c 2 .

Questo significa che – di nuovo – l’aumento di massa m è legato all’energia cinetica E da E=m c 2 .

In effetti, non è difficile dimostrare, usando un po’ di calcolo, che su tutto l’intervallo di velocità da zero alla velocità della luce, una particella in movimento sperimenta un aumento di massa legato alla sua energia cinetica da E=m c 2 . Per capire perché questo non viene notato nella vita quotidiana, provate un esempio, come un aereo a reazione che pesa 100 tonnellate e si muove a 2.000 miglia orarie. 100 tonnellate sono 100.000 chilogrammi, 2.000 miglia orarie sono circa 1.000 metri al secondo. Questo è un’energia cinetica 1 2 M v 2 di ½ ×1011joule, ma il corrispondente cambiamento di massa dell’aeroplano giù del fattore c 2 , 9× 10 16 , dando un aumento di massa effettiva di circa mezzo milligrammo, non troppo facile da rilevare!

E = mc2

Abbiamo visto sopra che quando una forza fa lavoro accelerando un corpo per dargli energia cinetica, la massa del corpo aumenta di una quantità pari al lavoro totale fatto dalla forza, l’energia E trasferita, divisa per c 2 . E quando una forza fa lavoro su un corpo che non lo sta accelerando, quindi non c’è aumento di energia cinetica? Per esempio, cosa succede se sollevo qualcosa ad una velocità costante, dandogli energia potenziale? Si scopre che anche in questo caso c’è un aumento di massa dato da E=m c 2 , naturalmente non misurabilmente piccolo per gli oggetti di tutti i giorni.

Tuttavia, questo è un effetto misurabile e importante nella fisica nucleare. Per esempio, l’elio-atomo ha un nucleo che ha due protoni e due neutroni legati insieme in modo molto stretto da una forte forza di attrazione nucleare. Se viene applicata una forza esterna sufficiente, questo può essere separato in due nuclei di “idrogeno pesante”, ognuno dei quali ha un protone e un neutrone. Si deve spendere molta energia esterna per ottenere questa separazione, e si scopre che la massa totale dei due nuclei di idrogeno pesante è misurabilmente (circa mezzo punto percentuale) più pesante del nucleo di elio originale. Questa extramassa, moltiplicata per c 2 , è uguale all’energia necessaria per dividere il nucleo di elio in due. Ancora più importante, questa energia può essere recuperata lasciando che i due idrogennuclei pesanti si scontrino e si uniscano per formare nuovamente un nucleo di elio. (Sono entrambi caricati elettricamente in modo positivo, quindi si respingono l’un l’altro, e devono unirsi abbastanza velocemente per superare questa repulsione e arrivare alla vicinanza in cui l’attrazione nucleare molto più forte entra in gioco). Questa è la fonte di energia di base della bomba all’idrogeno e del sole.

Si scopre che tutte le forme di energia, cinetica e diversi tipi di energia potenziale, hanno una massa associata data da E=m c 2 . Per le reazioni nucleari, il cambiamento di massa è tipicamente dell’ordine di un millesimo della massa totale, e facilmente misurabile. Per le reazioni chimiche, il cambiamento è dell’ordine di un miliardesimo della massa totale, e non è attualmente misurabile.

indice precedente